数据结构——三十四、Floyd算法(王道408)
文章目录
- 前言
- 一.Robert W. Floyd
- 二.Floyd算法原理
- 三.Floyd算法执行过程
- 1.例子
- 四.Floyd算法得到的结果的使用方法(下面有更详细的版本)
- 五.核心代码
- 1.代码展示
- 2.代码解释
- 六.复杂度
- 1.推导
- 2.结论
- 七.Floyd算法
- 1.例子(不用公式,只用思想)
- 2.使用方法
- 八.练习:Floyd算法用于负权图
- 九.Floyd算法的优势与局限性
- 十.知识点回顾与重要考点
- 结语
前言
Floyd算法是一种求解图中所有顶点对之间最短路径的动态规划算法。该算法由1978年图灵奖得主Robert W. Floyd提出,通过逐步增加中转顶点来优化路径长度。算法过程分为多个阶段:初始阶段基于邻接矩阵,随后每个阶段允许通过新增的中转顶点来更新最短路径。核心思想是比较直接路径和通过中转顶点的路径长度,若后者更优则更新矩阵。最终结果包含两个矩阵:存储最短路径长度和相应中转顶点。通过递归查询中转矩阵即可重构具体路径。该算法时间复杂度为O(n³),适用于解决带权图的最短路径问题。
一.Robert W. Floyd
- 罗伯特·弗洛伊德(1936—2001)Robert W. Floyd,1978年图灵奖得主
- Floyd算法(Floyd-Warshall算法)
- 堆排序算法
二.Floyd算法原理
- Floyd算法:求出每一对顶点之间的最短路径
- 使用动态规划思想,将问题的求解分为多个阶段,然后每个阶段之间有一个递进的关系
- 对于n个顶点的图G,求任意一对顶点Vi→Vj之间的最短路径可分为如下几个阶段:
- 初始:不允许这两个顶点之间的路径存在其他的中转顶点,最短路径是?
- 若允许V₀点作为它们之间的中转顶点,那最短路径会不会有进一步的优化呢?
- 若允许在V₀、V₁作为它们之间的中转顶点,那最短路径会不会有进一步的优化呢?
- 若允许在V₀、V₁、V₂作为它们之间的中转顶点,那最短路径会不会有进一步的优化呢?
- …
- 若允许在V₀、V₁、V₂……Vₙ-₁作为它们之间的中转顶点,那最短路径会不会有进一步的优化呢?
三.Floyd算法执行过程
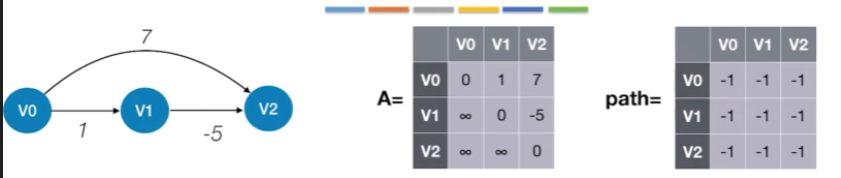
1.例子
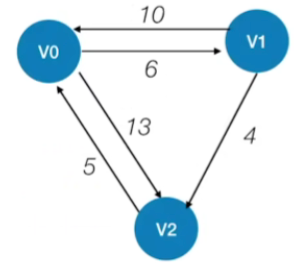
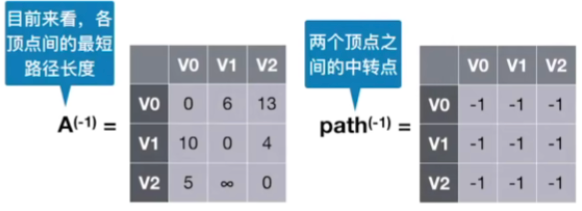
- 定义与初始化(状态-1):不允许各个顶点之间的路径存在其他的中转顶点
- 设置两个初始矩阵
- 第一个矩阵的初始状态其实与带权图的邻接矩阵相同,存储的是当前状态下各个顶点之间的最短路径长度,如在当前初始状态下,V0到V2的最短路径其实也就是13这一条
- 第二个矩阵path指的是我们目前能够找到的最短路径当中两个顶点之间的一个中转点,初始状态下所有顶点之间都不可以有中转点,所以我们初始的时候会把所有的这些path值都给设为-1
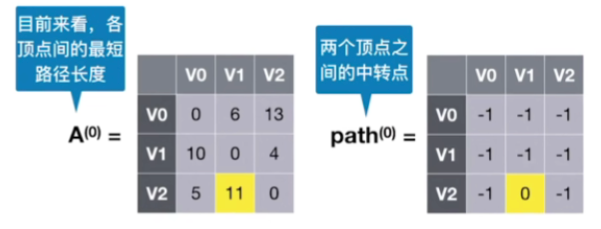
- 状态0:若允许在 V0V_{0}V0中转,最短路径是?——求 A(0)A^{(0)}A(0)和 path(0)path^{(0)}path(0)
- 遍历上一阶段留下来的这个矩阵A,对于矩阵A当中的每一个具体的元素,我们都需要进行这样的一个检查
- 比如说对于上一个状态的这个矩阵A我们检查它的A(−1)[2][1]A^{(-1)}[2][1]A(−1)[2][1]这个位置,也就是V2到V1的这条路径,以前我们不允许有中转点的时候,从V2到V1的最短路径长度是无穷,也就是没有直接相连的路径
- 但是现在我们考虑到能够以V0作为中转,那也就是说我们可以先从V2这个顶点先到达V0这个顶点,然后再从V0顶点到达V1这个顶点,这个路径长度是11,小于无穷
- 所以在加入了0号中转点之后,从V2到V1,我们能够找到的最短路径长度就变成了11,因此A(0)[2][1]A^{(0)}[2][1]A(0)[2][1]这个位置记录为11
- 那由于从V2到V1的时候,以0号作为中转点,所以我们把path(0)[2][1]path^{(0)}[2][1]path(0)[2][1]这个位置中转点记录为零,化为表达式为:{A(−1)[2][1]>A(−1)[2][0]+A(−1)[0][1]=11A(0)[2][1]=11path(0)[2][1]=0;\begin{cases}A^{(-1)}[2][1]>A^{(-1)}[2][0]+A^{(-1)}[0][1]=11 \\ A^{(0)}[2][1]=11 \\ path^{(0)}[2][1]=0;\end{cases}⎩⎨⎧A(−1)[2][1]>A(−1)[2][0]+A(−1)[0][1]=11A(0)[2][1]=11path(0)[2][1]=0;
- 抽象出通用表达式为:{若A(k−1)[i][j]>A(k−1)[i][k]+A(k−1)[k][j]则A(k)[i][j]=A(k−1)[i][k]+A(k−1)[k][j];path(k)[i][j]=k否则A(k)和path(k)保持原值注:k表示中转点\begin{cases}若A^{(k-1)}[i][j]>A^{(k-1)}[i][k]+A^{(k-1)}[k][j] \\ 则A^{(k)}[i][j]=A^{(k-1)}[i][k]+A^{(k-1)}[k][j];\\\quad path^{(k)}[i][j]=k \\ 否则A^{(k)}和path^{(k)}保持原值\\注:k表示中转点\end{cases}⎩⎨⎧若A(k−1)[i][j]>A(k−1)[i][k]+A(k−1)[k][j]则A(k)[i][j]=A(k−1)[i][k]+A(k−1)[k][j];path(k)[i][j]=k否则A(k)和path(k)保持原值注:k表示中转点
- 我们要更新下一个阶段,也就是k这个阶段的矩阵A和矩阵path,那我们需要基于上一个阶段的矩阵A进行一个条件的判断,如果满足这个条件的话,那我们就会把A和path对应位置的值进行A(k)[i][j]=A(k−1)[i][k]+A(k−1)[k][j];path(k)[i][j]=kA^{(k)}[i][j]=A^{(k-1)}[i][k]+A^{(k-1)}[k][j];path^{(k)}[i][j]=kA(k)[i][j]=A(k−1)[i][k]+A(k−1)[k][j];path(k)[i][j]=k的一个修改
- 当然对于这个矩阵当中的所有元素我们都需要循环的遍历一遍都需要进行A(k−1)[i][j]>A(k−1)[i][k]+A(k−1)[k][j]A^{(k-1)}[i][j]>A^{(k-1)}[i][k]+A^{(k-1)}[k][j]A(k−1)[i][j]>A(k−1)[i][k]+A(k−1)[k][j]的判断
- 那从初始的-1阶段到0号阶段,我们经过所有的检查之后,需要更新的也就只有刚才说到的这两个位置
- 状态1:若允许在V0V_{0}V0、V1V_{1}V1中转,最短路径是?——求A(1)A^{(1)}A(1)和path(1)path^{(1)}path(1)
- 和状态0时的思路一样,不做赘述,最终结果如下
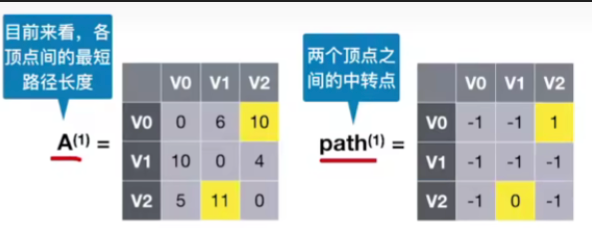
- 和状态0时的思路一样,不做赘述,最终结果如下
- 状态2:若允许在V0,V1,V2V_{0},V_{1},V_{2}V0,V1,V2中转,最短路径是?–求A(2)A^{(2)}A(2)和path(2)path^{(2)}path(2)
- 和之前一样,不做赘述
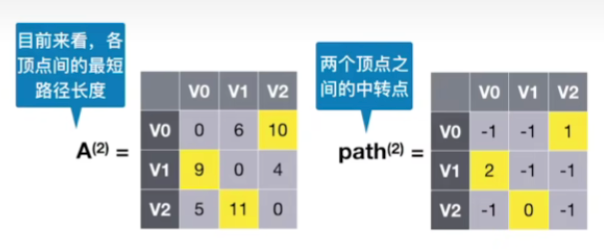
- 和之前一样,不做赘述
四.Floyd算法得到的结果的使用方法(下面有更详细的版本)
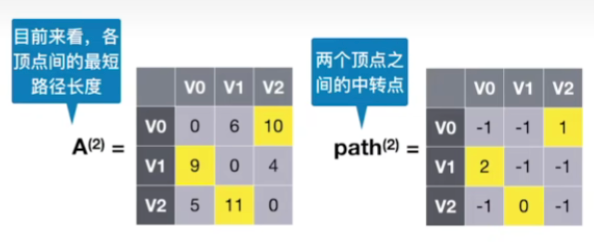
- 我们来找V0到V2的最短路径
- 那通过查A这个矩阵的对应位置得到这两个点之间最短路径长度应该是10
- 然后再查path的V0到V2,它们之间的中转点是1号中转点,所以V0到V2的最短路径应该是V0–>V1–>V2
五.核心代码
1.代码展示
//……准备工作,根据图的信息初始化矩阵A和 path(如上图)
for (int k=0; k<n; k++){ //考虑以Vk为中转点for(int i = 0; i < n; i++) //遍历整个矩阵,i为行号,j为列号for (int j=0; j<n; j++){ if (A[i][j]>A[i][k]+A[k][j]){ //以vk为中转点的路径更短A[i][j]=A[i][k]+A[k][j]; //更新最短路径长度path[i][j]=k; //中转点}}}
}
2.代码解释
- 刚开始的准备工作,需要准备一个矩阵A和矩阵path
- 矩阵A可以用图的邻接矩阵复制一份得到,path矩阵刚开始全部设为-1
- 接下来我们每一轮的处理当中都会考虑新增加一个新的中转点(Vk),那总共有n个顶点,所以最外层的循环我们需要循环n次
for (int k=0; k<n; k++) //考虑以Vk为中转点 - 那对于每一层的循环来说,也就是当我们新增加考虑一个中转点的时候,我们都需要检查A这个矩阵当中的各个元素,因此我们就需要把这个矩阵的所有的行,列都扫描一遍
for(int i = 0; i < n; i++) //遍历整个矩阵,i为行号,j为列号
for (int j=0; j<n; j++)
- 那对于这个矩阵当中的任何一个元素,我们都需要考虑这样的一个事情,i和j这两个顶点之间的最短路径如果新增加一个中转点k先到k这个顶点来中转的话那么有没有可能更小,如果会更小的话,我们就需要把A这个矩阵的信息给进行一个更新,带时path矩阵也需要记录我们这次新找到的这些更优的中转点
if (A[i][j]>A[i][k]+A[k][j]){ //以vk为中转点的路径更短A[i][j]=A[i][k]+A[k][j]; //更新最短路径长度path[i][j]=k; //中转点
}
六.复杂度
1.推导
- 显然总共有n层循环,每一层的循环都是会循环n2n^2n2次,整个算法的时间复杂度就应该是n3n^3n3
- 由于我们需要建立这样的两个辅助的矩阵,它们的大小都是n行n列,所以空间复杂度应该是n2n^2n2
2.结论
- 时间复杂度,O(|V|³)
- 空间复杂度,O(|V|²)
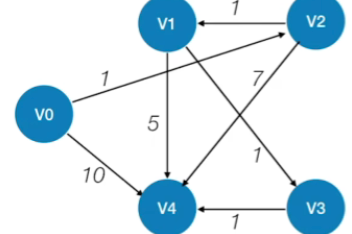
七.Floyd算法
1.例子(不用公式,只用思想)
注意:此例子旨在理解Floyd中的矩阵蕴藏的信息与原图的联系,非必要无需用这种方法来计算矩阵中的值
- 初始(状态-1):没有中转点
- A矩阵可以通过图的邻接矩阵得到,path矩阵全是-1

- A矩阵可以通过图的邻接矩阵得到,path矩阵全是-1
- 状态0:V0作为中转点
- 因为V0没有入边,说明没有任何顶点能借助V0中转,因此不用改变A矩阵和path矩阵(后面不再对V0进行讨论)
- 状态1:V0,V1作为中转点
- V1的入边有V2,说明V2可能通过V1中转到达V3或V4
- 假设V2->V1->V4,得到V2到V4的路径长度是6,而A表中的V2到V4最短路径长度是7,因此需要更改A[2][4]为6,同时将path[2][4]为1
- 假设V2->V1->V3,得到V2到V3的路径长度是2,而A表中的V2到V3的最短路径长度是∞,因此需要更改A[2][3]为2,同时将path[2][3]为1
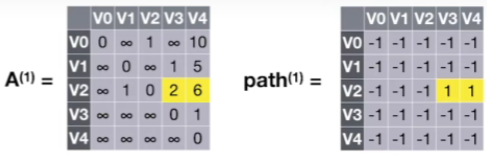
- 状态2:V0,V1,V2作为中转点
- 只有V2做中转点
- 可以看出V2只有一条入边V0->V2,因此V0可以借助V2作为中转点到V4或者到V1
- 不难算出V0->V2->V1的路径长度为2,而矩阵A中的A[0][1]为∞,因此更改A[0][1]为2,path[0][1]为2
- 同样的方式得到V0->V2->V4的路径长度为8,而矩阵A中的A[0][4]为10,因此更改A[0][4]为8,path[0][4]为2
- 以V1,V2做中转点
- 当用V1,V2作为中转点时,我们可以先看看,在path表中V2借助V1作为中转点已经找到了最优的到达V3和V4的路径,因此在考虑到借助V2和V1作为中转点时,可以当做一个整体来考虑,权值大小在矩阵A中可以找到
- 将V2->V1作为一个整体设为V,通过观察矩阵A与矩阵path可以得到V->V3的最短路径长度为2,V->V4的最短路径长度为6
- 于是通过作为V唯一的入边V0->V,V0->V->V4的路径长度为1+6 = 7<A[0][4] = 8,因此替换A[0][4]为7,path[0][4]为V中的第一个顶点,即2
- 同样的V0->V->V3的路径长度为1+2 = 3 < A[0][3] = ∞,因此替换A[0][3]为3,path[0][3]为V中的第一个顶点,即2

- 只有V2做中转点
- 状态3:V0,V1,V2,V3作为中转点
- 和之前的操作一样,不再赘述,其结果如下:
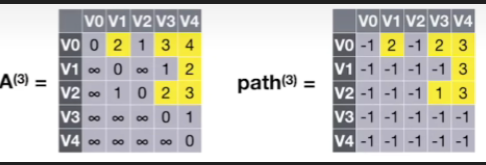
- 和之前的操作一样,不再赘述,其结果如下:
- 状态4.V0,V1,V2,V3,V4作为中转点
- 和之前的操作一样,不再赘述,其结果如下:
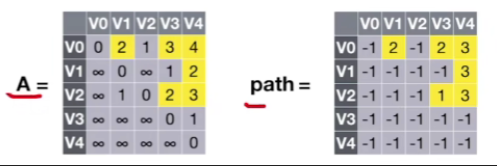
- 和之前的操作一样,不再赘述,其结果如下:
2.使用方法
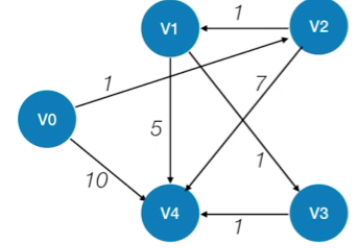
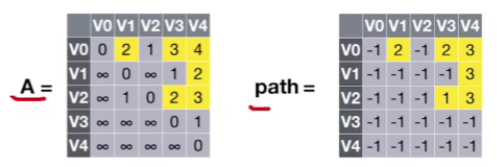
- 找V0到V4的最短路径
- V0到V4中间需要有一个中转点V3,也就是说V0需要先到V3,然后V3再到V4,但是通过看图得知V0到V3并没有一条直接存在的路径

- 所以其实V0到V3的最短路径,我们还需要在迭代的往里边填充一些中转顶点,通过查看矩阵path得知V0->V3还需要经过中转点V2
- 通过查看path表得知V3到V4的最短路径中间是没有中转点的,所以这两个节点之间我们不需要再加任何东西
- 同样查看path得知V0->V2之间没有中转点,所以这两个节点之间我们不需要再加任何东西(path[0][2] = -1)

- 在接下来还需要看V2到V3,他们中间有中转点V1
- 加入V1,分别查看V1->V2和V1->V3是否有中转点,通过path表得知已经没有中转点

- 综合起来就是,V0->V4的最短路径为:V0->V2->V1->V3->V4

- V0到V4中间需要有一个中转点V3,也就是说V0需要先到V3,然后V3再到V4,但是通过看图得知V0到V3并没有一条直接存在的路径
八.练习:Floyd算法用于负权图
九.Floyd算法的优势与局限性
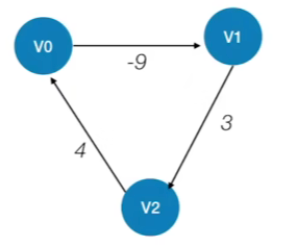
- Floyd算法不能解决带有“负权回路”的图(有负权值的边组成回路),这种图有可能没有最短路径
- Floyd算法可以用于负权值带权图
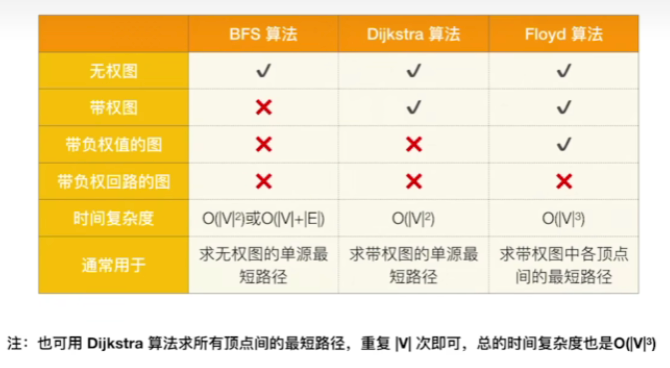
十.知识点回顾与重要考点
结语
二更😉
如果想查看更多章节,请点击:一、数据结构专栏导航页