当前位置：首页 > news >正文

计算机图形学：【Games101】学习笔记03——光栅化（三角形的离散化、深度测试与抗锯齿）

news 2025/10/31 9:46:46

计算机图形学：【Games101】学习笔记03——光栅化（三角形的离散化、深度测试与抗锯齿）

前言
一、光栅化（三角形的离散化）
- 1.1 透视投影（Perspective Projection）
- 1.2 视口变换：标准立方体到屏幕（Canonical Cube to Screen）
- 1.3 光栅化基础：从三角形到像素（Triangles、Samping）
- - 1.3.1 三角形：基础图元(Triangles - Fundamental Shape Primitives)
  - 1.3.2 光栅化的核心逻辑：2D 采样
  - 1.3.3 统一所有 2D 变换
  - 1.3.4 光栅化的问题：走样（Aliasing）与锯齿（Jaggies）
  - 1.3.5 补充：常见的光栅显示器
二、光栅化（深度测试与抗锯齿）
- 2.1 走样（Aliasing）
- - 2.1.1 走样的常见现象
  - 2.1.2 走样的本质：信号采样理论
- 2.2 反走样（Anti-Aliasing）
- - 2.2.1 反走样的理论逻辑：预滤波（Pre-Filtering）
  - 2.2.2 图形学中的预滤波：像素区域平均
  - 2.2.3 实用反走样方法：超采样（SSAA）与多重采样（MSAA）
  - 2.2.4 其他反走样技术简介
三、疑难点整理总结
写在最后

前言

🎮 GAMES101 是国内相当有名的图形学公开课。项目相关资源在：https://sites.cs.ucsb.edu/~lingqi/teaching/games101.html。
本 📒笔记为 🖊️笔者在自学过程中整理的 🇨🇳中文版笔记，供各位 📖读者阅读 😼～
从这一讲开始，我们正式进入计算机图形学的核心模块 ——光栅化（Rasterization）。光栅化是 “将 2D 图形图元（如三角形）转换为屏幕像素” 的关键技术，也是游戏等实时渲染场景的核心。本讲先补全 “视图变换管线的最后一步（视口变换）”，再聚焦三角形光栅化的基本原理、采样逻辑与优化方法，内容相对直观，下面逐模块梳理。

一、光栅化（三角形的离散化）

1.1 透视投影（Perspective Projection）

上一讲已推导透视投影矩阵，但未明确 “如何通过视角（fovY）和宽高比（aspect）定义视锥体”，同时还需补充 “标准立方体到屏幕” 的视口变换，这两部分是光栅化前的最后准备。
实际应用中，我们不会直接指定视锥体的左（l）、右（r）、下（b）、上（t）边界，而是通过更直观的垂直视场角（fovY）和屏幕宽高比（aspect）推导，前提是视锥体 “左右对称（l=-r）” 和 “上下对称（b=-t）”。
在这里插入图片描述

1. 关键参数定义

垂直视场角（fovY）：相机沿 y 轴方向的视野范围，即近平面上下边界与相机连线的夹角；
宽高比（aspect）：屏幕宽度与高度的比值（aspect = width /height）；
近平面距离（|n|）：相机到近平面的距离（因相机看向 - Z 轴，n 为负值，|n | 为实际距离）。

2. 推导过程（How to convert from fovY and aspect to l, r, b, t?）

1️⃣ 求上边界 t：从相机原点看向近平面，y 轴方向的三角形为直角三角形（对边为 t，邻边为 | n|，锐角为 fovY/2），根据正切函数： $tan⁡(fovY2)=t∣n∣⟹t=∣n∣⋅tan⁡(fovY2)\tan\left(\frac{\text{fovY}}{2}\right) = \frac{t}{|n|} \implies t = |n| \cdot \tan\left(\frac{\text{fovY}}{2}\right)$ 。因上下对称，下边界 b = -t；
2️⃣ 求右边界 r：根据宽高比定义（aspect = 宽度 / 高度），而宽度 = r - l = 2r（l=-r），高度 = t - b = 2t（b=-t），因此： $aspect=2r2t=rt⟹r=t⋅aspect\text{aspect} = \frac{2r}{2t} = \frac{r}{t} \implies r = t \cdot \text{aspect}$ 。因左右对称，左边界 l = -r。

1.2 视口变换：标准立方体到屏幕（Canonical Cube to Screen）

视口变换（Viewport Transformation）是 “视图 - 投影管线” 的最后一步，将标准立方体 $1,1]^3$ 的 xy 平面（2D 投影结果）映射到屏幕像素坐标系，实现 “从数学坐标到屏幕像素” 的转换。

1. 屏幕坐标系的定义

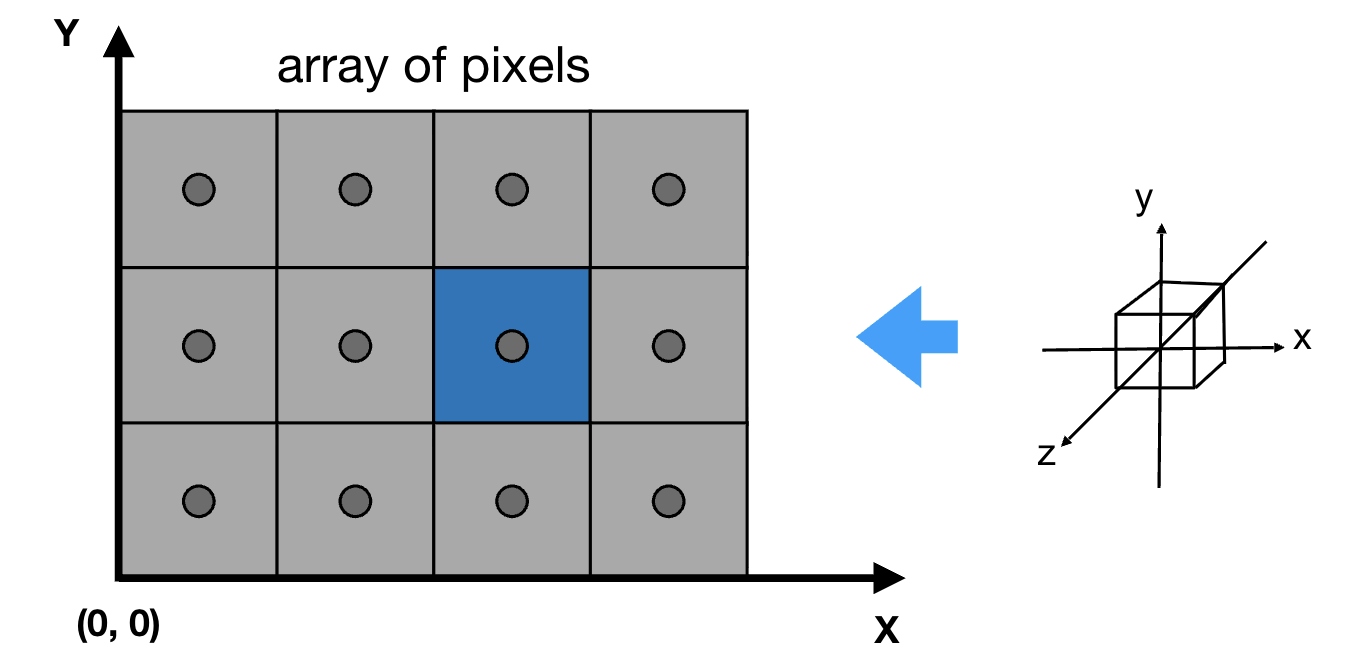
屏幕：由像素组成的 2D 数组，分辨率为 width × height（如 1920×1080，width=1920 为像素列数，height=1080 为像素行数）；
像素坐标：像素索引为整数，范围从 (0, 0)（屏幕左上角）到 (width-1, height-1)（屏幕右下角）；
每个像素的 “采样中心” 坐标为 (x+0.5, y+0.5)（如像素 (0,0) 的中心在 (0.5, 0.5)，避免采样点落在像素边缘）；
屏幕的整体范围为 (0, 0) 到 (width, height)（覆盖所有像素的中心）。

2. 视口变换的目标

将标准立方体 xy 平面的 $1,1]^2$ 范围，映射到屏幕的 $[0, w i d t h] \times [0, h e i g h t]$ 范围，z 坐标暂时无关（后续用于深度测试）。

3. 视口变换矩阵 $M_{viewport}$

变换分为 “缩放” 和 “平移” 两步，最终 4×4 齐次矩阵为： $Mviewport=[width200width20height20height200100001]M_{viewport} = \begin{bmatrix} \frac{\text{width}}{2} & 0 & 0 & \frac{\text{width}}{2} \\ 0 & \frac{\text{height}}{2} & 0 & \frac{\text{height}}{2} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$
缩放逻辑：将 [-1,1] 的长度（2 个单位）缩放到屏幕的 width/height 长度，缩放因子为 width/2（x 轴）和 height/2（y 轴）；
平移逻辑：将缩放后的范围（x 从 - width/2 到 width/2，y 从 - height/2 到 height/2）平移到屏幕的 [0, width] × [0, height] ，平移量为 width/2（x 轴）和 height/2（y 轴）；
示例：标准坐标 (-1, -1)（左下）经变换后为 (0, 0)（屏幕左下），标准坐标 (1, 1)（右上）经变换后为 (width, height)（屏幕右上），符合预期。
4. 完整的视图 - 投影管线

至此，3D 点到屏幕像素的完整变换流程为：
$3D点→建模变换Mmodel世界坐标→视图变换Mview相机坐标→投影变换Mproj标准立方体→视口变换Mviewport屏幕坐标\text{3D点} \xrightarrow{\text{建模变换}M_{model}} \text{世界坐标} \xrightarrow{\text{视图变换}M_{view}} \text{相机坐标} \xrightarrow{\text{投影变换}M_{proj}} \text{标准立方体} \xrightarrow{\text{视口变换}M_{viewport}} \text{屏幕坐标}$ 。

最终得到三角形顶点的屏幕坐标，为后续光栅化做好准备。

1.3 光栅化基础：从三角形到像素（Triangles、Samping）

光栅化的核心是 “将 2D 图形图元（如三角形）转换为屏幕上的像素集合”，而三角形是图形学中最常用的图元，原因在于其独特的几何性质。

1.3.1 三角形：基础图元(Triangles - Fundamental Shape Primitives)

三角形是光栅化的 “最优图元”，主要有 4 个关键原因：

最基本的多边形：任何复杂多边形（如四边形、五边形）都可拆分为多个三角形；
保证平面性：三个点必然共面，不会出现 “非平面多边形”（如四边形可能因顶点不在同一平面导致渲染错误）；
内部定义明确：三角形的内部和外部有清晰的数学判断方法（如叉积）；
便于插值：可通过重心坐标（Barycentric Coordinates）在三角形内部平滑插值颜色、纹理坐标、法向量等属性。

1.3.2 光栅化的核心逻辑：2D 采样

光栅化本质是 “对三角形的 2D 指示函数进行采样”—— 判断每个像素的中心是否在三角形内部，若在则为该像素分配颜色，否则不分配。

2D 指示函数的定义

定义二元函数 $inside(tri,x,y)\text{inside}(tri, x, y)$ ，表示点 (x,y) 是否在三角形 tri 内部： $inside(tri,x,y)={1若(x,y)在三角形内部或边上0否则\text{inside}(tri, x, y) = \begin{cases} 1 & \text{若}(x,y)\text{在三角形内部或边上} \\ 0 & \text{否则} \end{cases}$
光栅化就是对这个函数在 “所有像素中心” 进行采样，采样结果为 1 的像素即为三角形覆盖的像素。

采样流程（伪代码）:

// 遍历屏幕所有像素
for (int x = 0; x < width; ++x) {for (int y = 0; y < height; ++y) {// 计算当前像素的中心坐标float sampleX = x + 0.5f;float sampleY = y + 0.5f;// 判断中心是否在三角形内，是则标记像素if (inside(triangle, sampleX, sampleY)) {image[x][y] = triangleColor; // 为像素分配三角形颜色}}
}

在这里插入图片描述

如何判断点是否在三角形内部？—— 叉积法：光栅化的关键步骤，利用 “叉积判断向量方向” 的性质，通过三次叉积即可确定点与三角形的位置关系。

设三角形的三个顶点为 $P_0, P_1, P_2$ ，待判断的点为Q：
1. 计算三个边对应的向量叉积：

$c0⃗=P0P1⃗×P0Q⃗\vec{c_0} = \vec{P_0P_1} \times \vec{P_0Q}$ （判断 Q 相对于边 $P_0P_1$ 的方向）；
$c1⃗=P1P2⃗×P1Q⃗\vec{c_1} = \vec{P_1P_2} \times \vec{P_1Q}$ （判断 Q 相对于边 $P_1P_2$ 的方向）；
$c2⃗=P2P0⃗×P2Q⃗\vec{c_2} = \vec{P_2P_0} \times \vec{P_2Q}$ （判断 Q 相对于边 $P_2P_0$ 的方向）；
若三个叉积的符号一致（均为正或均为负，忽略零值的边情况），则 Q 在三角形内部；否则在外部。

2. 边情况处理（Edge Cases）
当 Q 落在三角形的边上时，可能被两个相邻三角形同时判断为 “内部”，导致像素重复着色。解决方法是制定 “边归属规则”，例如：

仅当点落在边的 “右侧” 或 “上侧” 时，才判定为属于该三角形；
确保每条边仅归属一个三角形，避免重复采样。

1.3.3 统一所有 2D 变换

此时，缩放、旋转、剪切也可升级为 3×3 矩阵，与平移统一：

缩放（Scale）： $S(sx,sy)=[1a0010001]S(s_x,s_y) = \begin{bmatrix} 1 & a & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$
旋转（Rotation）： $R(α)=[sx000sy0001]R(\alpha) = \begin{bmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \end{bmatrix}$
平移（Translation）： $T(tx,ty)=[10tx01ty001]T(t_x,t_y) = \begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{bmatrix}$

这种 “线性变换 + 平移” 的组合，称为仿射变换（Affine Transformation） —— 齐次坐标的核心价值就是将仿射变换统一为单一矩阵乘法。

1.3.4 光栅化的问题：走样（Aliasing）与锯齿（Jaggies）

虽然基本光栅化能将三角形转换为像素，但会产生明显的 “锯齿”，这是采样过程中 “走样” 现象的体现。
在这里插入图片描述
走样（Aliasing）是 “连续信号离散化采样时，因采样频率不足导致的失真”，在光栅化中表现为：三角形的边缘呈现 “阶梯状”（锯齿，Jaggies）；

原因：屏幕分辨率有限（采样频率固定），无法完美还原三角形的连续边缘，高频细节（如尖锐边缘）被低频信号（像素方块）替代。

在这里插入图片描述

1.3.5 补充：常见的光栅显示器

显示器类型	原理	应用场景
阴极射线管（CRT）	电子束扫描屏幕，激发荧光粉发光，采用隔行扫描模式	早期电视、显示器
液晶显示器（LCD）	通过液晶扭转偏振光控制透光率，背光照射产生图像	笔记本电脑、手机、显示器
有机发光二极管（OLED）	有机材料通电发光，无需背光，对比度更高	高端手机、电视
电子墨水屏（E-Ink）	微胶囊内黑白粒子受电场控制翻转，反射环境光显示	电子书（如 Kindle）

二、光栅化（深度测试与抗锯齿）

2.1 走样（Aliasing）

要解决锯齿问题，首先需要理解 “走样” 的本质 —— 它不是图形学特有的问题，而是信号采样过程中频率不匹配导致的失真。

2.1.1 走样的常见现象

在计算机图形学中，走样以多种形式出现，核心都是 “高频信号被低频采样误导”：

锯齿（Jaggies）：三角形边缘的阶梯状失真，是空间采样不足导致的走样；

摩尔纹（Moiré Patterns）：拍摄密集网格或条纹时出现的彩色干涉图案，是图像 undersampling（采样频率低于信号频率）导致的走样；

车轮幻觉（Wagon Wheel Illusion）：视频中车轮看似 “倒转” 或 “静止”，是时间采样不足导致的走样（采样频率低于车轮旋转的频率）。

这些现象的共同原因：信号变化速度（高频）超过了采样速度（低频），导致高频信号被错误地还原为低频信号，即 “频率混叠”。

2.1.2 走样的本质：信号采样理论

为理解走样，需先掌握信号采样的核心概念 —— 频率、采样率、Nyquist 频率，这些是反走样技术的理论基础。

（1）信号的频率：变化快慢的度量

定义：信号在单位时间 / 空间内的变化次数，频率越高，信号变化越剧烈；
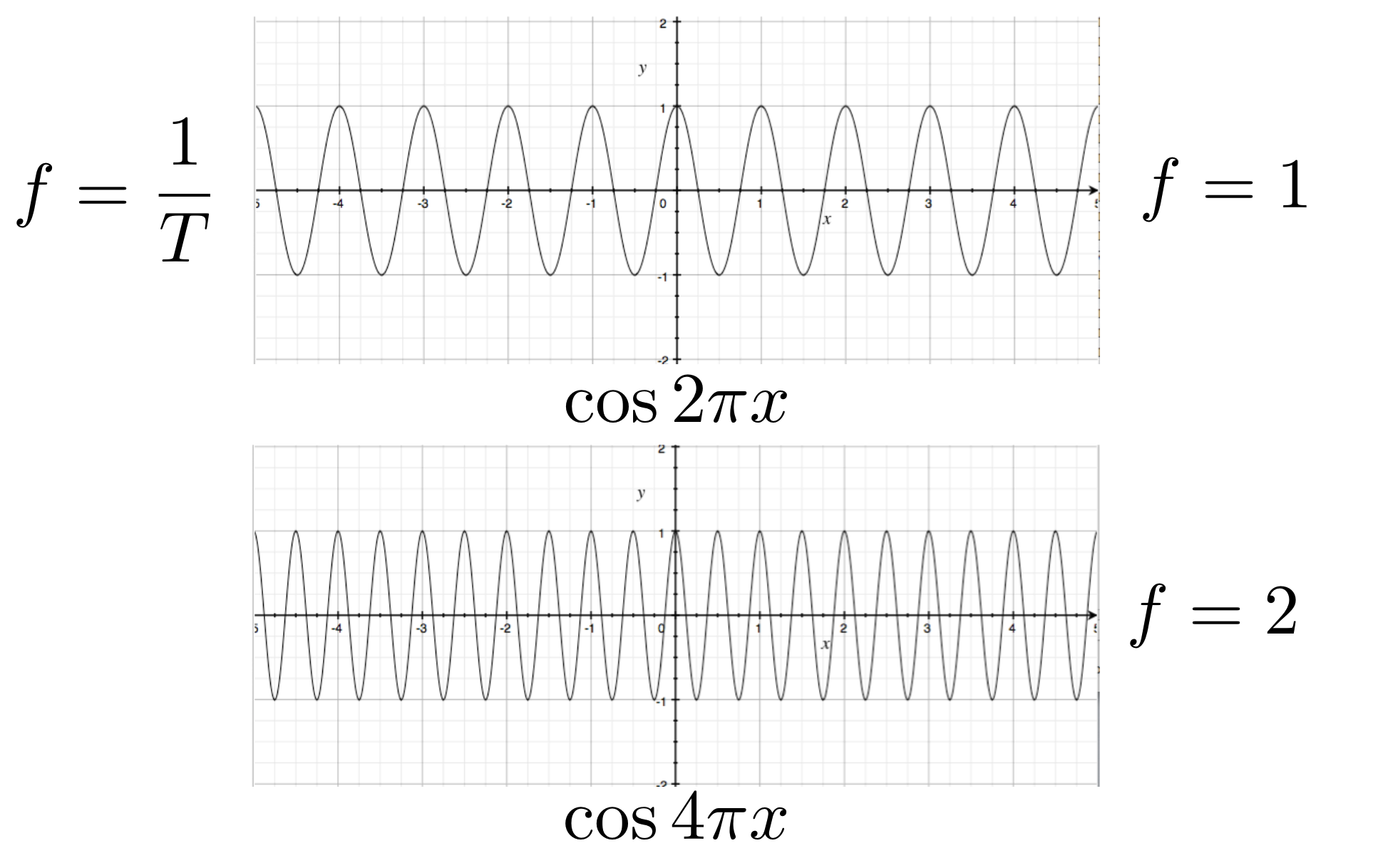
例：1D 信号中， $cos⁡(2πx)\cos(2\pi x)$ 的频率为 1（每秒变化 1 次）， $cos⁡(4πx)\cos(4\pi x)$ 的频率为 2（每秒变化 2 次，变化更剧烈）；
图形学中的 “高频信号”：三角形边缘（颜色从背景色突变到三角形色）、密集纹理、细小物体等。

（2）采样率与 Nyquist 频率

采样率（Sampling Rate）：单位时间 / 空间内的采样次数（如屏幕分辨率 1920×1080，空间采样率为 1920 像素 / 宽度）；
Nyquist 定理：要无失真地还原信号，采样率必须至少是信号最高频率的 2 倍（即采样率 $fs≥2fmaxf_s \geq 2f_{max}$ ），其中 $f_{max}$ 是信号的最高频率， $f_s/2$ 称为Nyquist 频率；
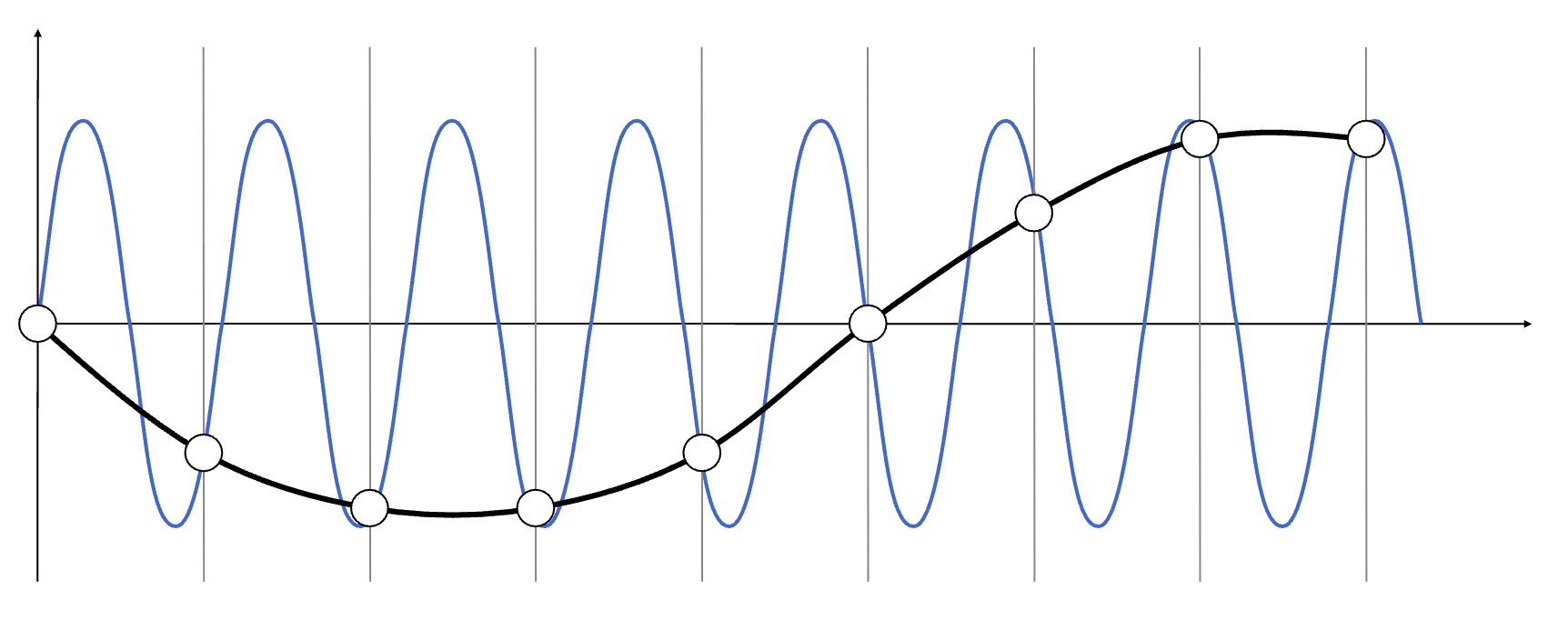
走样的根源：当采样率 $f_s < 2f_{max}$ 时，高频信号会 “折叠” 到低频区域，导致采样结果无法还原原信号，产生混叠（Aliasing）。

（3）图形学中的走样：空间采样不足

三角形边缘是典型的 “高频信号”（颜色在边缘处突变），而屏幕的像素采样率是固定的（如 1080P 屏幕的垂直采样率为 1080）。当边缘与像素网格不平行时，采样率低于边缘的 “空间频率”，导致边缘被采样为阶梯状（锯齿），即空间走样。

2.2 反走样（Anti-Aliasing）

反走样的核心思路是 “先滤波，再采样”—— 通过过滤掉信号中的高频成分，使信号最高频率低于 Nyquist 频率，再进行采样，从而避免频率混叠。

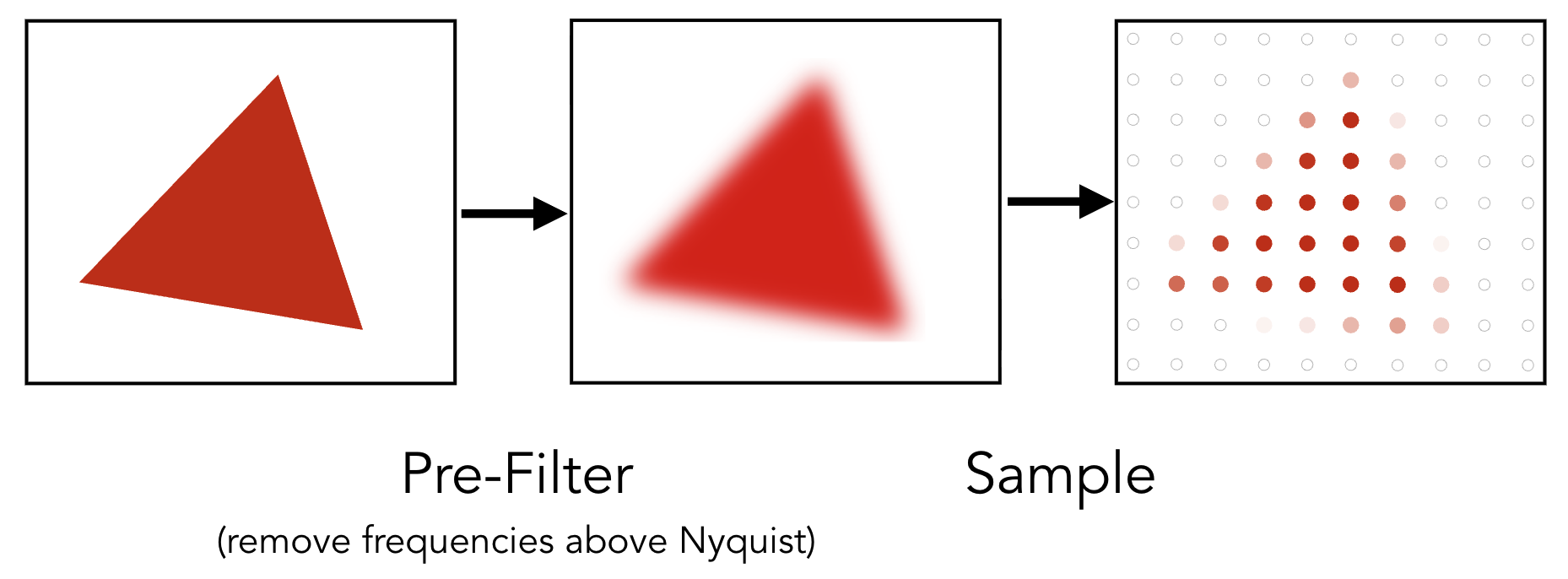
2.2.1 反走样的理论逻辑：预滤波（Pre-Filtering）

滤波（Filtering）：去除信号中不需要的频率成分，图形学中常用低通滤波（Low-Pass Filtering）——保留低频信号，过滤高频信号（如模糊处理，软化边缘，降低信号变化速度）；
预滤波（Pre-Filtering）：在采样前对原始信号进行低通滤波，确保信号最高频率低于 Nyquist 频率，再进行采样；
错误做法：先采样后滤波：若先采样（已产生走样），再对采样结果滤波（如模糊像素），只能模糊锯齿，无法消除走样根源；
正确做法：先滤波后采样：对连续的三角形信号先进行低通滤波（模糊边缘），再采样，此时边缘颜色从三角形色平滑过渡到背景色，锯齿自然消失。

2.2.2 图形学中的预滤波：像素区域平均

在三角形光栅化中，“预滤波” 的实际操作是计算像素被三角形覆盖的面积比例—— 像素颜色的透明度（或强度）与覆盖面积成正比，实现 “颜色平滑过渡”。

核心原理：原始光栅化中，像素颜色是 “非黑即白”（要么完全属于三角形，要么不属于），而反走样中，像素颜色是 “渐变的”：若像素 100%
被三角形覆盖，颜色为三角形纯色；若像素 50% 被覆盖，颜色为三角形色与背景色的混合（如 50% 透明）；若像素 0%被覆盖，颜色为背景色；
本质：将 “点采样”（仅判断中心）升级为 “区域采样”（计算覆盖面积），相当于用 “1 像素大小的盒式滤波器（Box Filter）” 对信号进行预滤波。
问题：计算覆盖面积成本高：直接计算像素与三角形的重叠面积（如积分计算）在实时渲染中效率过低，因此需要更高效的近似方法 ——超采样（Supersampling, SSAA）。

2.2.3 实用反走样方法：超采样（SSAA）与多重采样（MSAA）

超采样是 “区域采样的近似实现”，通过在单个像素内采集多个样本点，用样本点的 “内外比例” 近似覆盖面积，从而实现反走样。

超采样（Supersampling, SSAA）

核心逻辑：
提高采样率：在每个像素内均匀采集 N×N 个样本点（如 2×2、4×4）；
判断样本归属：对每个样本点，用叉积判断是否在三角形内；
平均计算像素颜色：像素颜色 =（三角形内样本数 / 总样本数）× 三角形色 +（背景样本数 / 总样本数）× 背景色；

示例（2×2 超采样）：像素内采集 4 个样本点，若 2 个在三角形内，则像素颜色为 “50% 三角形色 + 50% 背景色”，边缘呈现半透明过渡，锯齿消失；

优点：反走样效果好，逻辑直观；
缺点：性能成本高 ——N×N 超采样的计算量是原采样的 N² 倍（如 4×4 超采样需多计算 16 倍的样本点），实时渲染（如游戏）中难以承受。

多重采样（Multisampling, MSAA）：SSAA 的优化版

SSAA 的痛点是 “对所有像素都进行高频率采样”，但实际上只有边缘像素需要多采样，内部像素 100% 被覆盖，无需多采样。MSAA 通过 “共享样本 + 仅存储深度 / 模板信息” 优化性能：
核心改进：
样本点共享：相邻像素共享边缘的样本点（如 2×2 MSAA 中，4 个像素共享 4 个样本点，而非每个像素单独 4 个）；
仅对边缘像素计算颜色：内部像素只需 1 个样本点判断归属，边缘像素根据样本点比例混合颜色；
存储优化：仅存储样本点的深度（Z 值）和模板（Stencil）信息，颜色信息按像素存储，减少内存占用；

优点：反走样效果接近 SSAA，但性能成本远低于 SSAA，是游戏和实时渲染中最常用的反走样技术；
常见参数：2×MSAA、4×MSAA、8×MSAA，采样数越多，反走样效果越好，但性能消耗也越高。

2.2.4 其他反走样技术简介

除了 SSAA 和 MSAA，还有多种针对不同场景的反走样方法，GAMES 101课程提及了三类：

FXAA（Fast Approximate AA）：快速近似反走样，在光栅化后对图像进行边缘检测和模糊处理，性能消耗极低，但效果略逊于 MSAA，适合性能有限的设备；
TAA（Temporal AA）：时间性反走样，利用相邻帧的采样信息（如第 1 帧采样像素左上，第 2 帧采样右上），通过时间累积实现反走样，可在低采样率下获得接近高 MSAA 的效果，广泛用于 3A 游戏；
DLSS（Deep Learning Super Sampling）：深度学习超采样，利用 AI 模型将低分辨率图像 upscale（放大）到高分辨率，并同时消除锯齿，兼顾性能和画质，是近年来的热门技术（如 NVIDIA 的 DLSS 3）。

反走样的核心结论

没有免费的午餐：反走样效果与性能成本成正比，需根据应用场景（实时 / 离线）选择合适的方法；
离线渲染（如电影）：可使用高倍 SSAA 或光线追踪中的自适应采样，追求极致画质；
实时渲染（如游戏）：优先选择 MSAA、TAA 或 DLSS，在画质和性能间平衡。