平方数和分组

前言：这两道题都有向上取整和向下取整的意思。

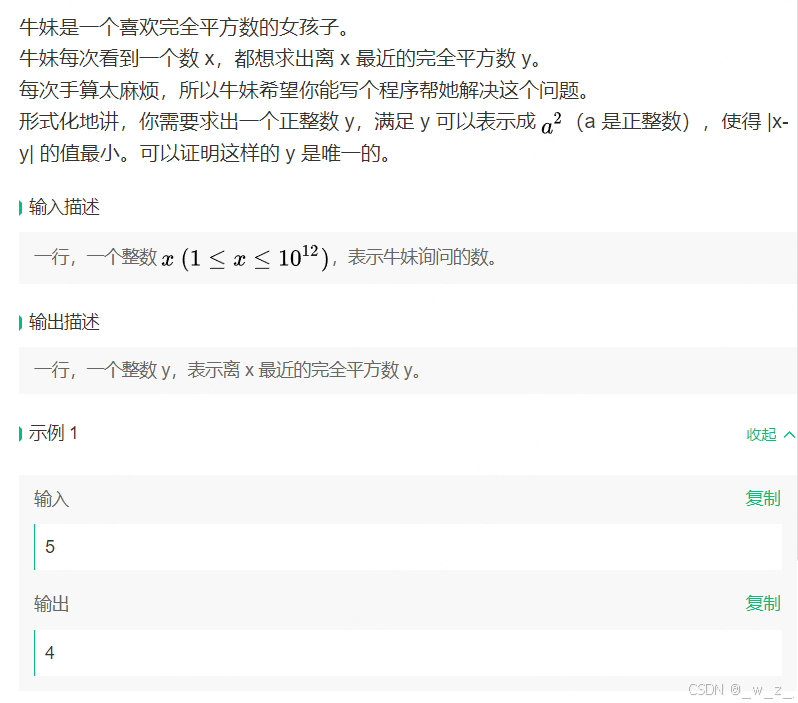
其实就是简单的数学问题，通过开根号，找到离自己最近的完全平方数的根，再求完全平方：

#include<bits/stdc++.h>using namespace std;int main() {long long a;while (cin >> a) { // 注意 while 处理多个 caselong long n = sqrt(a);long long b = n * n;long long c = (n + 1) * (n + 1);if (c - a > a - b)cout << b << endl;elsecout << c << endl;}
}

这个题其实一开始我想到了要用二分法，苦于自己数学思维逻辑太差了。

这个题就是找最小的“人数最多的小组人数”，我们先统计每个声部的人数，然后从人数最多的声部开始，把它作为每组人数上限的初始值capacity。接着，我们定义一个函数：对于当前每组最多人数 capacity，计算每个声部需要分成多少组（人数除以 x 向上取整），把所有声部需要的组数加起来得到总组数。如果总组数不超过 m，说明这个上限可行，我们就尝试减小每组人数(capacity--)，让每组尽可能少人；如果总组数超过 m，说明人数太少，无法安排，就停止搜索。最终，能满足条件的最小上限就是“人数最多的小组人数”。如果一开始 m 小于声部数，则无法安排，直接返回 -1。

#include <bits/stdc++.h>using namespace std;
int n, m;
unordered_map<int, int>hx;bool check(int capacity) {int sum = 0;for (auto& e : hx) {sum = sum + e.second / capacity + (e.second % capacity == 0 ? 0 : 1);}return sum <= m;
}int main() {cin >> n >> m;int max_capacity = 0;for (int i = 0; i < n; i++) {int x;cin >> x;max_capacity = max(max_capacity, ++hx[x]);}if (m < hx.size())cout << -1;else {int l = 1;int r = max_capacity;while (l < r) {int mid = (l + r) / 2;if (check(mid)) r = mid;else l = mid + 1;}cout << l;}}

而二分法呢，先确定答案的可能范围 [1, 最大声部人数]，每次取中间值 mid 作为候选每组人数，计算总组数是否满足 ≤ m。如果满足，就说明可以尝试更小的每组人数，把右边界缩小到 mid；如果不满足，就说明人数太少无法安排，把左边界移到 mid + 1。不断折半缩小区间，直到左右边界重合，此时得到的值就是最小可行的“人数最多的小组人数”。相比暴力搜索，二分法通过每次排除一半区间，大大提高了搜索效率。这里说一下为什么sum<=m也是可以的，因为当组数小于m时，就说明当前 x 是可行的(可以正常分组)，还有可能找到更小的每组人数，使得总组数仍然 ≤ m，我们的目标是使x最小，x越小，m就可能会越大。

几点说明：

1.以后再有map这种关联式的代码，可以用一个循环就搞定，不用再存数组再搞一个循环。

        int x;
cin >> x;
        max_capacity = max(max_capacity, ++hx[x]);

2.二分法，一般都是左闭右开，当不满足条件时，往往是l==r

3.e.second / capacity + (e.second % capacity == 0 ? 0 : 1);可以作为向上取整的方式

a/b -------> a/b+(a%b==0?0:1)