数据结构(13)
目录
一、图的连通性
1、无向图的连通性
(1) 连通图(Connected Graph)
(2)连通分量(Connected Component)
2、有向图的连通性
(1)强连通图(Strongly Connected Graph)
(2)强连通分量(Strongly Connected Component, SCC)
(3)弱连通图(Weakly Connected Graph)
3、连通性的判断方法
4、连通性的意义
二、图的连通性问题
1. 生成树的定义
2. 遍历生成树的形成过程
3. 深度优先搜索生成树(DFS 树)
4. 广度优先搜索生成树(BFS树)
5.DFS树和BFS树的对比
三、非连通图的遍历与生成树
1. 生成森林的定义
2. 生成森林的形成过程
3. 示例
四、生成树/森林的核心特性
五、意义与应用
一、图的连通性
图的连通性是描述图中顶点之间 “可达性” 的核心概念,即判断任意两个顶点之间是否存在至少一条路径(由边或弧连接而成),它是分析图结构和功能的基础,分为无向图的连通性和有向图的连通性两类,定义和判断标准有所不同。
1、无向图的连通性
无向图中,边没有方向(顶点 A 到 B 的边与 B 到 A 的边等价),连通性的定义更直观,核心是 “双向可达”。
(1) 连通图(Connected Graph)
若无向图中任意两个不同的顶点之间,都存在至少一条路径,则称该无向图为连通图。
- 示例:包含顶点 {0,1,2,3}、边 {(0,1),(1,2),(2,3)} 的图是连通图 ——0 到 3 有路径 0→1→2→3,1 到 3 有路径 1→2→3,任意顶点间均可达。
- 关键特征:整个图是一个 “不可分割” 的连通整体,不存在孤立的顶点子集(与其他顶点无路径相连)。
(2)连通分量(Connected Component)
若无向图不是连通图,则图中 “最大的连通子图”(无法再添加其他顶点仍保持连通)称为连通分量。
- 每个连通分量自身是连通图,且不同连通分量之间无任何路径(顶点不共享,边不连接)。
- 示例:包含顶点 {0,1,2,3,4}、边 {(0,1),(1,2),(3,4)} 的图,有两个连通分量 —— 分量 1(顶点 {0,1,2})、分量 2(顶点 {3,4}),0 到 3 之间无路径。
- 特殊情况:完全孤立的单个顶点(无任何边),自身也是一个连通分量。
2、有向图的连通性
有向图中,边有方向(弧 <A,B> 表示从 A 到 B 的单向路径,B 到 A 需单独的弧 < B,A>),连通性需区分 “单向可达” 和 “双向可达”,定义更精细。
(1)强连通图(Strongly Connected Graph)
若有向图中任意两个不同的顶点 A 和 B 之间,既存在从 A 到 B 的路径,也存在从 B 到 A 的路径(双向可达),则称该有向图为强连通图。
- 示例:包含顶点 {0,1,2}、弧 {<0,1>,<1,2>,<2,0>} 的图是强连通图 ——0→1→2→0,1→2→0→1,任意顶点间双向可达。
- 关键特征:边的方向形成 “闭环”,确保顶点间无单向阻断。
(2)强连通分量(Strongly Connected Component, SCC)
若有向图不是强连通图,则图中 “最大的强连通子图”(无法再添加其他顶点仍保持强连通)称为强连通分量。
- 每个强连通分量自身是强连通图,不同分量之间可能存在单向路径,但无双向路径。
- 示例:包含顶点 {0,1,2,3}、弧 {<0,1>,<1,0>,<1,2>,<2,3>} 的图,有三个强连通分量 —— 分量 1({0,1},双向可达)、分量 2({2},孤立顶点)、分量 3({3},孤立顶点),0 到 2 有路径(0→1→2),但 2 到 0 无路径。
(3)弱连通图(Weakly Connected Graph)
若忽略有向图中边的方向(将弧视为无向边)后,图是连通图,则称原有的向图为弱连通图。
- 弱连通图不要求顶点间双向可达,仅要求 “忽略方向后能连通”,可能存在单向路径的阻断。
- 示例:包含顶点 {0,1,2}、弧 {<0,1>,<1,2>} 的图,忽略方向后是连通的(0-1-2),但 2 到 0 无路径,因此是弱连通图,不是强连通图。
3、连通性的判断方法
判断图的连通性,本质是判断顶点间的可达性,核心工具是图的遍历算法(DFS/BFS):
(1)无向图连通性判断:
从任意一个顶点出发,执行 DFS 或 BFS,若遍历结束后所有顶点均被访问,则图是连通图;否则不是,未访问的顶点属于其他连通分量。
(2)有向图强连通性判断:
方法 1(暴力法):对每个顶点执行 DFS/BFS,检查是否能到达所有其他顶点,若所有顶点均满足,则是强连通图(时间复杂度较高,适合小规模图)。
方法 2(高效法):用 Kosaraju 算法、Tarjan 算法等,通过 1-2 次 DFS 即可找出所有强连通分量(时间复杂度 O (n+e),适合大规模图)。
4、连通性的意义
连通性是图的核心属性,直接决定图的功能和应用:
- 网络领域:判断通信网络是否 “无死角”(任意节点可通信)、道路网络是否 “互联互通”。
- 算法领域:是生成树 / 森林、最短路径、拓扑排序等算法的前提(如拓扑排序仅适用于有向无环图,且需先确保图的连通性或处理分量)。
- 数据结构领域:连通分量的划分可用于聚类(如社交网络中划分 “好友圈子”)。
二、图的连通性问题
问:对连通图进行遍历,得到的是什么?
得到的将是一个极小连通子图,即图的生成树:
(1)由DFS得到的生成树称为深度优先搜索生成树
(2)由BFS得到的生成树称为广度优先搜索生成树
1. 生成树的定义
对于一个连通图(任意两顶点间都有路径),其生成树是包含原图所有顶点的一个极小连通子图:
- 包含所有顶点:生成树的顶点集与原图完全一致。
- 极小连通:用最少的边保持连通性(边数 = 顶点数 - 1),且删除任何一条边都会导致子图不连通,添加任何一条原图中未包含的边都会形成环。
2. 遍历生成树的形成过程
当用 DFS 或 BFS 遍历连通图时,遍历过程中首次访问顶点所经过的边会构成一棵生成树:
- 这些边称为 “树边”(Tree Edge),是遍历过程中 “发现新顶点” 的关键路径。
- 未被纳入生成树的边称为 “非树边”(如回边、交叉边),它们在遍历中不会用于发现新顶点(因顶点已被访问)。
3. 深度优先搜索生成树(DFS 树)
- 形成逻辑:由 DFS 遍历中 “首次访问顶点的路径” 构成,体现深度优先的探索特征(沿一条路径深入,遇阻后回溯)。
- 示例:连通图 G 有顶点 {0,1,2,3},边 (0,1),(0,2),(1,3),(2,3)。从 0 出发的 DFS 过程中,首次访问路径为:0→1→3→2,对应的树边为 (0,1),(1,3),(3,2)(或 (0,1),(1,3),(0,2),取决于邻接顺序),形成 DFS 树:
0/1/
3
特点:树的结构可能因邻接顶点的访问顺序不同而变化,但一定是“深度优先”的分支结构(可能存在较长的单链)。
4. 广度优先搜索生成树(BFS树)
形成逻辑:由BFS遍历中“首次访问顶点的路径”构成,体现广度优先的层次特征(按距离起始顶点的远近逐层扩展)。
示例: 同上连通图,从0出发的BFS过程中,首次访问路径为:$0→1, 0→2, 1→3$,对应的树边为 $(0,1),(0,2),(1,3)$
特点:树的层次清晰,顶点的深度(与根的距离)等于该顶点在原图中到起始顶点的最短路径长度(无权图),结构相对“扁平”。
5.DFS树和BFS树的对比
| 特性 | DFS 树 | BFS 树 |
|---|---|---|
| 结构特征 | 深度优先,分支可能较长(单链状) | 广度优先,层次清晰(扁平状) |
| 顶点深度含义 | 深度由递归栈深度决定,不直接对应最短路径 | 深度等于顶点到根的最短路径长度(无权图) |
| 非树边类型 | 无向图只有回边,有向图有回边和交叉边 | 无向图可能有跨层边,有向图多为跨层边 |
三、非连通图的遍历与生成树
对非连通图进行遍历,得到的将是各连通分量的生成树,即图的生成森林
1. 生成森林的定义
对于非连通图(存在至少两个顶点无路径相连,即由多个连通分量组成),遍历所有顶点后,每个连通分量会生成一棵生成树,这些生成树的集合称为生成森林。
(1)生成森林包含原图所有顶点,且每个连通分量对应一棵生成树。
(2)生成森林的边数 = 总顶点数 - 连通分量数(每棵树的边数为“顶点数 - 1”,总和为“总顶点数 - 连通分量数”)。
2. 生成森林的形成过程
非连通图的遍历需对每个未访问的顶点(即每个连通分量的起始点)分别执行DFS或BFS:
(1)每个连通分量的遍历会生成一棵生成树(DFS树或BFS树)。
(2)所有连通分量的生成树共同组成生成森林,树与树之间无连接(因原连通分量间无路径)。
3. 示例
非连通图 $G$ 包含两个连通分量:
(1)分量1:顶点 $\{0,1,2\}$,边 $(0,1),(1,2)$;
(2)分量2:顶点 $\{3,4\}$,边 $(3,4)$。
遍历过程:
(1)从0出发DFS,生成分量1的DFS树:$0→1→2$(树边:$(0,1),(1,2)$)。
(2)发现未访问顶点3,从3出发DFS,生成分量2的DFS树:$3→4$(树边:$(3,4)$)。
(3)生成森林由两棵树组成:$\{0-1-2, 3-4\}$。
例题:
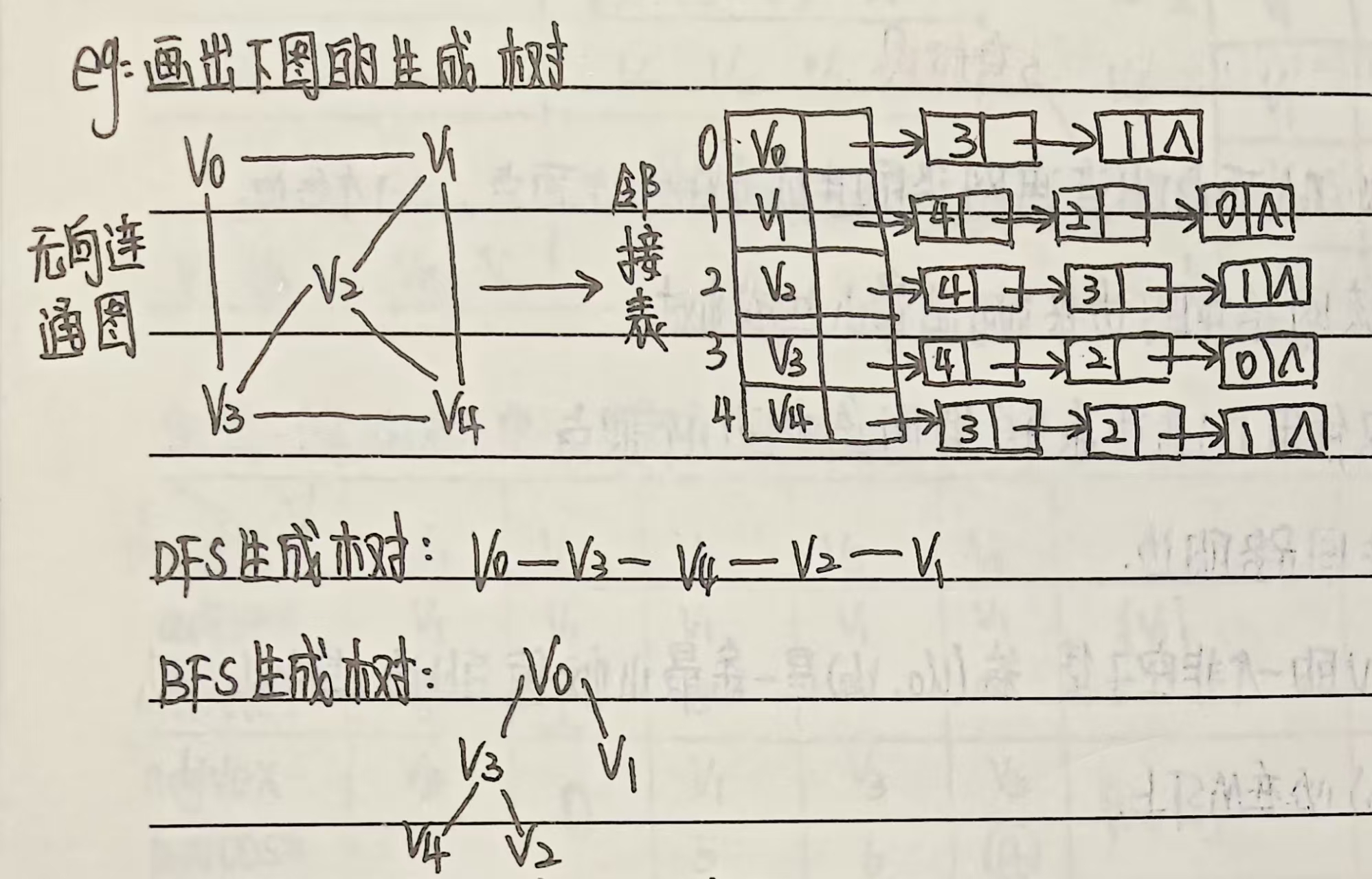
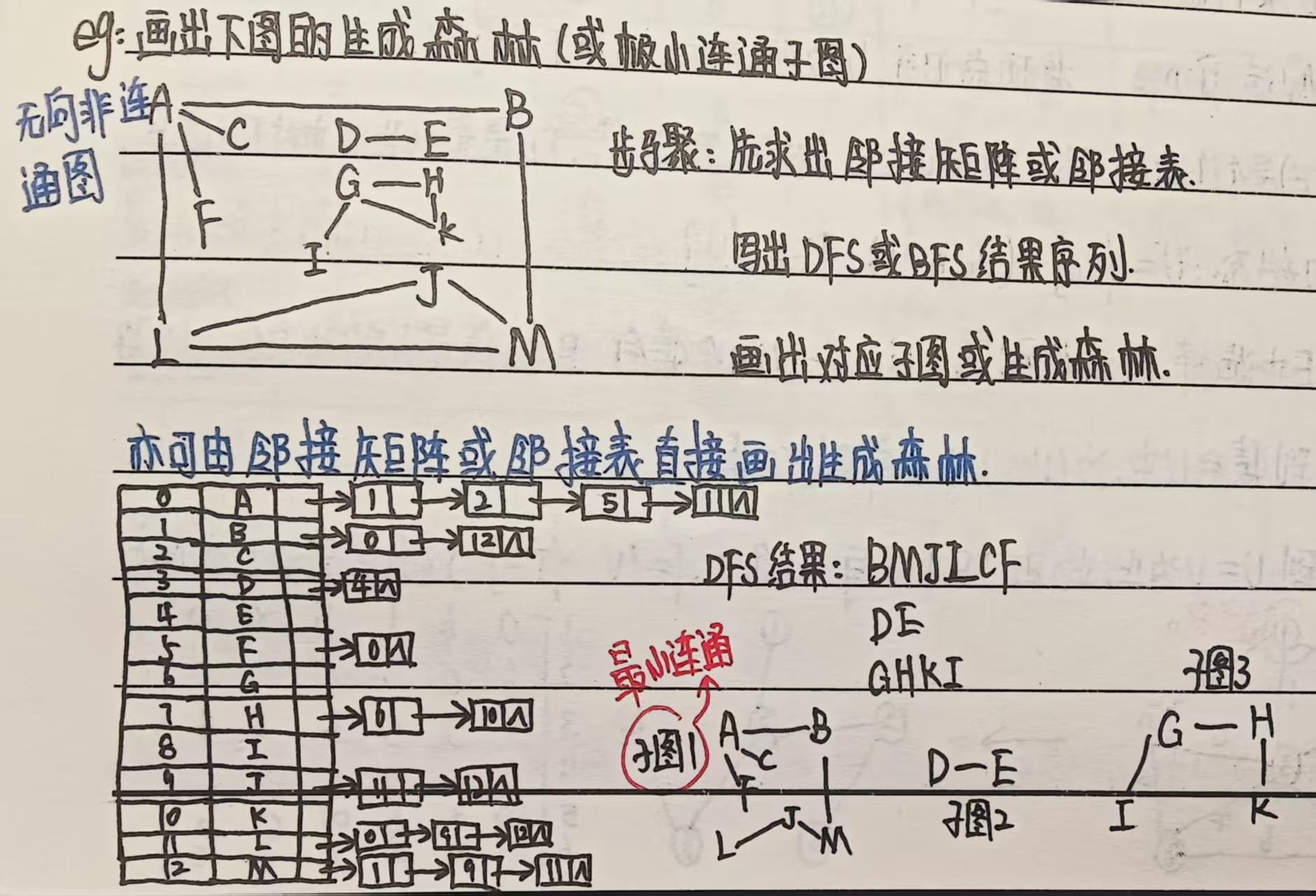
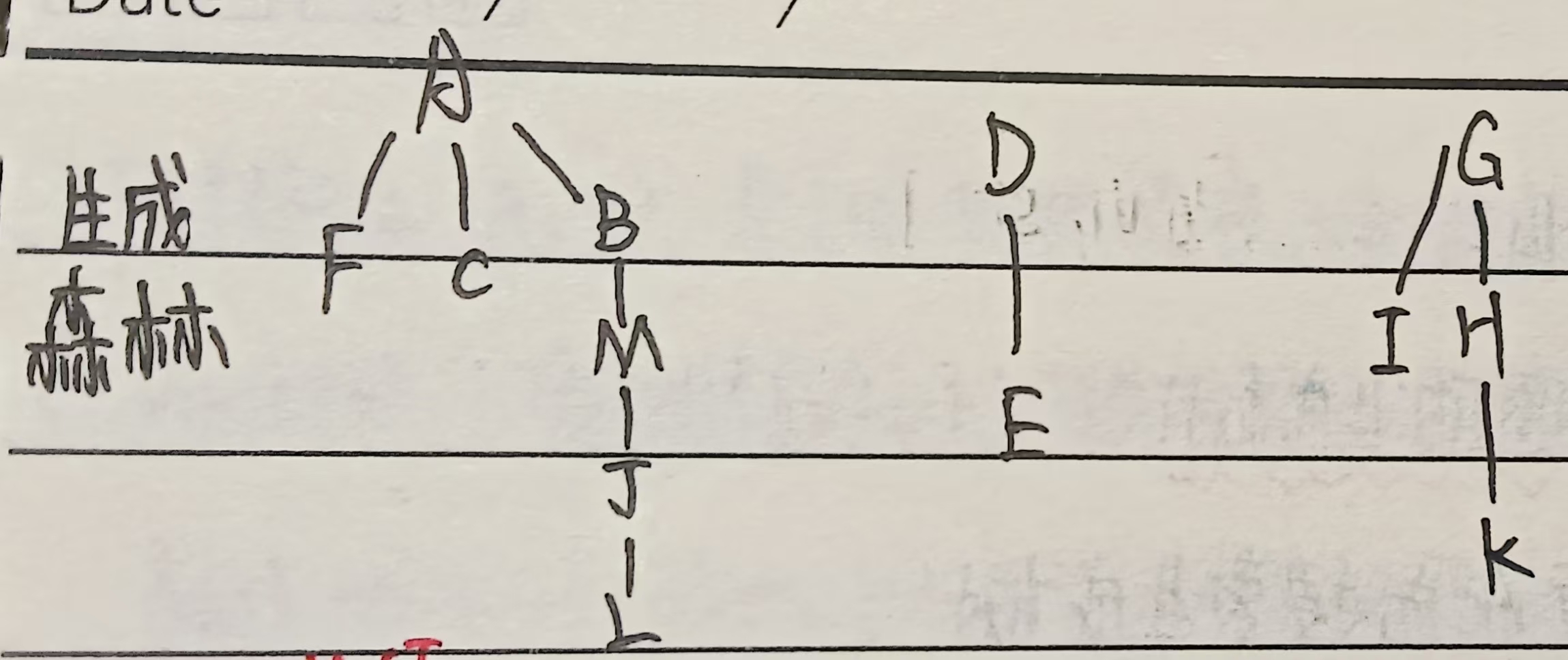
四、生成树/森林的核心特性
1. 保留连通性:生成树保留了原连通分量的连通性,生成森林保留了原图各连通分量的独立连通性。
2. 边数最少:是包含所有顶点的连通子图中边数最少的(删除任何边会破坏连通性)。
3. 无环性:生成树/森林中一定无环(若有环,则不符合“边数最少”的极小性)。
4. 与遍历方式相关:同一图的DFS生成树和BFS生成树结构可能不同,但顶点集完全一致。
五、意义与应用
1、连通性验证:生成树的存在证明原图(或分量)是连通的;生成森林的树数量等于原图的连通分量数。
2、优化存储:用生成树/森林表示图可减少边的存储量(仅保留必要的树边),适合稀疏图的高效处理。
3、算法基础:是最小生成树(MST)、最短路径树等进阶算法的基础,在网络布线、路径规划等领域有直接应用。
