1.1 神经网络基本组成

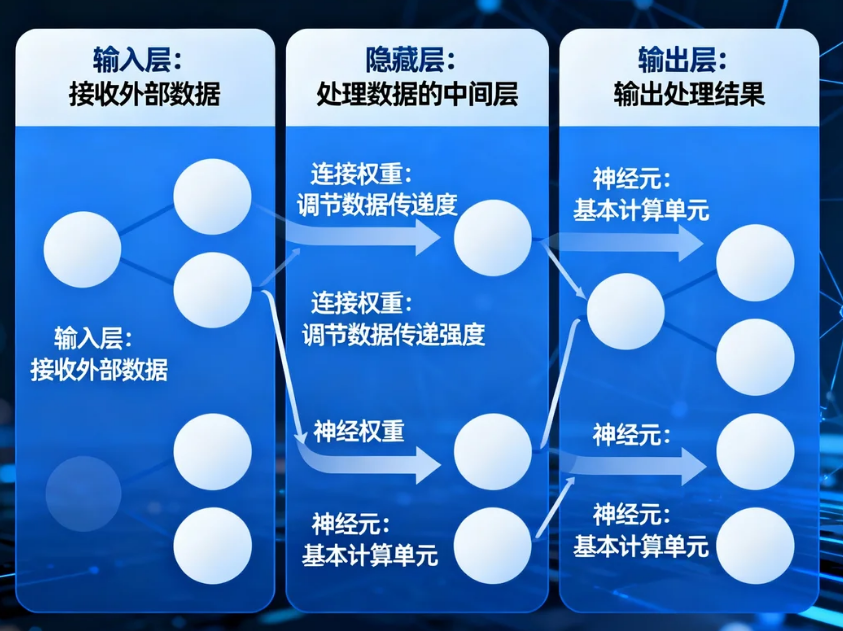
1.1.1 神经元和层的概念

什么是神经元？

生物神经元类比：

• 就像大脑中的神经细胞，接收信号、处理信号、传递信号
• 人工神经元模拟这个过程

数学表示：
一个神经元执行两个主要操作：

1. 加权求和：z = w₁x₁ + w₂x₂ + ... + wₙxₙ + b
2. 激活函数：a = f(z)

# Python代码示例：手动实现一个神经元
import numpy as npdef simple_neuron(inputs, weights, bias, activation_function):"""简单神经元实现inputs: 输入信号列表 [x1, x2, ..., xn]weights: 权重列表 [w1, w2, ..., wn]  bias: 偏置项activation_function: 激活函数"""# 步骤1：加权求和weighted_sum = np.dot(weights, inputs) + bias# 步骤2：应用激活函数output = activation_function(weighted_sum)return output# 示例使用
def sigmoid(x):return 1 / (1 + np.exp(-x))inputs = [0.5, 0.3, 0.8]
weights = [0.4, 0.7, 0.2]
bias = 0.1output = simple_neuron(inputs, weights, bias, sigmoid)
print(f"神经元输出: {output:.4f}")

什么是神经网络层？

层的类型：

1. 输入层：接收原始数据
2. 隐藏层：进行特征提取和转换
3. 输出层：产生最终预测

层的数学表示：
对于有 m 个输入和 n 个神经元的层：

输出 = 激活函数(权重矩阵 × 输入向量 + 偏置向量)

# Python代码示例：实现一个完整的神经网络层
class DenseLayer:def __init__(self, input_size, output_size, activation_function):# 初始化权重和偏置self.weights = np.random.randn(output_size, input_size) * 0.1self.bias = np.zeros((output_size, 1))self.activation = activation_functiondef forward(self, inputs):# 前向传播self.inputs = inputsself.z = np.dot(self.weights, inputs) + self.biasself.output = self.activation(self.z)return self.output# 示例：创建一个有3个输入、4个神经元的层
layer = DenseLayer(3, 4, sigmoid)
inputs = np.array([[0.5], [0.3], [0.8]])  # 3个输入特征
outputs = layer.forward(inputs)
print(f"层输出形状: {outputs.shape}")
print(f"层输出值: {outputs.flatten()}")

1.1.2 前向传播与反向传播

前向传播 (Forward Propagation)

定义：数据从输入层流向输出层的过程

过程描述：

1. 输入数据进入输入层
2. 每层对输入进行加权求和并应用激活函数
3. 结果传递到下一层，直到输出层

# 前向传播示例
class SimpleNetwork:def __init__(self):self.layer1 = DenseLayer(3, 4, sigmoid)  # 输入层到隐藏层self.layer2 = DenseLayer(4, 2, sigmoid)  # 隐藏层到输出层def forward(self, x):# 数据流经网络h1 = self.layer1.forward(x)output = self.layer2.forward(h1)return output# 使用网络
network = SimpleNetwork()
input_data = np.array([[0.1], [0.2], [0.3]])
prediction = network.forward(input_data)
print(f"网络预测: {prediction.flatten()}")

反向传播 (Backward Propagation)

定义：误差从输出层反向传播到输入层，用于更新权重

核心思想：链式法则

∂Loss/∂w = ∂Loss/∂output × ∂output/∂z × ∂z/∂w

反向传播步骤：

1. 计算输出层误差
2. 将误差反向传播到隐藏层
3. 计算每个权重的梯度
4. 更新权重

# 反向传播的数学理解
def backward_propagation_example():"""简化版反向传播示例"""# 假设我们有一个简单的网络：x -> w -> z -> a -> Lossx = 2.0    # 输入w = 0.5    # 权重y_true = 1.0  # 真实值# 前向传播z = w * x        # 加权求和a = sigmoid(z)   # 激活函数输出loss = (a - y_true) ** 2  # 损失函数（均方误差）print(f"前向传播结果: z={z:.3f}, a={a:.3f}, loss={loss:.3f}")# 反向传播 - 计算梯度# 链式法则：dLoss/dw = dLoss/da * da/dz * dz/dwdLoss_da = 2 * (a - y_true)           # ∂Loss/∂ada_dz = a * (1 - a)                   # ∂a/∂z (sigmoid导数)dz_dw = x                             # ∂z/∂wdLoss_dw = dLoss_da * da_dz * dz_dw   # ∂Loss/∂wprint(f"权重梯度: {dLoss_dw:.3f}")# 更新权重learning_rate = 0.1w_new = w - learning_rate * dLoss_dwprint(f"更新后的权重: {w_new:.3f}")backward_propagation_example()

1.1.3 权重和偏置的作用

权重 (Weights) 的作用

功能：

• 控制输入信号的重要性
• 决定神经元对不同输入的敏感程度

数学意义：

• 权重 wᵢ 乘以输入 xᵢ
• 权重越大，该输入对神经元输出的影响越大

# 权重影响的演示
def demonstrate_weights():# 相同输入，不同权重inputs = np.array([0.5, 0.3])# 情况1：第一个输入权重较大weights1 = np.array([0.9, 0.1])  # 更关注第一个特征output1 = np.dot(weights1, inputs)# 情况2：第二个输入权重较大  weights2 = np.array([0.1, 0.9])  # 更关注第二个特征output2 = np.dot(weights2, inputs)print(f"权重分布1 [0.9, 0.1]: 输出 = {output1:.3f}")print(f"权重分布2 [0.1, 0.9]: 输出 = {output2:.3f}")print("→ 权重决定了网络关注哪些特征")demonstrate_weights()

偏置 (Bias) 的作用

功能：

• 调整神经元的激活阈值
• 使神经元可以灵活地学习模式

数学意义：

• 偏置 b 加到加权和上：z = w·x + b
• 控制神经元何时"激活"

# 偏置影响的演示
def demonstrate_bias():inputs = np.array([0.5, 0.3])weights = np.array([0.4, 0.6])# 不同偏置值的影响biases = [-1, 0, 1]for bias in biases:z = np.dot(weights, inputs) + biasa = sigmoid(z)activation_status = "激活" if a > 0.5 else "未激活"print(f"偏置={bias}: z={z:.3f}, a={a:.3f} ({activation_status})")demonstrate_bias()

权重和偏置的学习过程

# 完整的权重更新过程示例
class LearningProcess:def __init__(self):self.weights = np.array([0.3, 0.7])self.bias = 0.1def train_step(self, x, y_true, learning_rate=0.1):# 前向传播z = np.dot(self.weights, x) + self.biasy_pred = sigmoid(z)# 计算损失loss = (y_pred - y_true) ** 2# 反向传播计算梯度dloss_dpred = 2 * (y_pred - y_true)dpred_dz = y_pred * (1 - y_pred)dz_dw = xdz_db = 1# 权重和偏置的梯度dloss_dw = dloss_dpred * dpred_dz * dz_dwdloss_db = dloss_dpred * dpred_dz * dz_db# 更新参数self.weights -= learning_rate * dloss_dwself.bias -= learning_rate * dloss_dbreturn loss, y_pred# 训练过程演示
def training_demonstration():model = LearningProcess()# 训练数据X = [np.array([0.2, 0.8]), np.array([0.7, 0.3]), np.array([0.9, 0.1])]Y = [1, 0, 0]  # 目标输出print("训练过程:")print("初始 - 权重:", model.weights, "偏置:", model.bias)for epoch in range(3):  # 3个训练周期total_loss = 0for i, (x, y_true) in enumerate(zip(X, Y)):loss, y_pred = model.train_step(x, y_true)total_loss += lossprint(f"  样本{i}: 预测={y_pred:.3f}, 目标={y_true}, 损失={loss:.3f}")print(f"周期 {epoch+1} - 权重: {model.weights}, 偏置: {model.bias:.3f}")print(f"总损失: {total_loss:.3f}\n")training_demonstration()

关键概念总结

神经元工作流程：

输入 → 加权求和 → 激活函数 → 输出x₁, x₂, ..., xₙ → ∑(wᵢxᵢ) + b → f(z) → a

前向传播 vs 反向传播：

方面	前向传播	反向传播
方向	输入→输出	输出→输入
目的	计算预测值	计算梯度
数据流	输入数据	误差信号
计算	加权求和+激活函数	链式法则求导

权重和偏置的角色：

• 权重：特征重要性调节器
• 偏置：激活阈值调节器
• 共同作用：使神经网络能够学习复杂的模式