《小白学随机过程》第二章：常见的随机过程——详细解读马尔科夫决策过程MDP和强化学习(2 值迭代和策略迭代 附python代码

上篇文章第二章：常见的随机过程——详细解读马尔科夫决策过程MDP和强化学习(1)挖了一个大坑，文章提到：

1. 马尔可夫决策过程（$MarkovDecisionProcess,MDP$）是强化学习的理论基础。$MDP$ 的求解目标是找到一个最优策略 ${\pi }^{\ast }$，使得从任意状态出发，智能体获得的期望累积回报（通常为折扣回报）最大。

2. 根据是否已知 $MDP$ 的完整模型（即状态转移概率 $P(s^{\prime }\mid s,a)$ 和奖励函数 $R(s,a)$），求解方法可分为两大类：基于模型的求解方法（$Model-BasedMethods$）和无模型的求解方法（$Model-FreeMethods$）

3. 假设环境模型已知（即 $P$ 和 $R$ 已知），可通过动态规划等方法精确求解。常见的方法有基于动态规划的值迭代（$ValueIteration$）或策略迭代（$PolicyIteration$）方法。

本章准备填上这个坑，首先开始从环境模型已知的情况开始讲起。

---

首先需要完全理解+熟悉掌握几个公式，这是进一步学习的基础。如果你对下述表格内容非常熟悉，可以直接跳到《如何求解贝尔曼最优函数》章节，否则建议首先搞清楚这几个公式(专业名词)的含义

概念	定义	对应贝尔曼方程
状态值函数 $V^{\pi }(s)$	策略 $\pi$ 下从状态 $s$ 开始的期望回报	贝尔曼期望方程 (for $V^{\pi }$)
动作值函数 $Q^{\pi }(s,a)$	策略 $\pi$ 下在 $s$ 采取 $a$ 后的期望回报	贝尔曼期望方程 (for $Q^{\pi }$)
最优状态值函数 $V^{\ast }(s)$	所有策略中从 $s$ 开始的最大期望回报	贝尔曼最优方程 (for $V^{\ast }$)
最优动作值函数 $Q^{\ast }(s,a)$	所有策略中在 $s$ 采取 $a$ 后的最大期望回报	贝尔曼最优方程 (for $Q^{\ast }$)

---

值函数

下面我们用一个机器人在 $5\times 5$ 网格地图上进行路径规划的经典例子，详细说明 状态值函数（$State-ValueFunction$） 和 动作值函数（$Action-ValueFunction/Q$ 函数） 的含义、计算方式以及它们在强化学习中的作用。

例子设定

• 网格大小：$5\times 5$，坐标范围是 $(0,0)$ 到 $(4,4)$
• 起点：$s_0=(0,0)$
• 终点：$s_{\text{goal}}=(4,4)$
• 移动方向：机器人可以向四个方向移动：{上、下、左、右}\{上、下、左、右\}{上、下、左、右}（假设无对角移动）
• 奖励机制：
  • 每次移动消耗能量 → 奖励为负值（如 $-1$）
  • 到达终点奖励 $+10$
• 折扣因子：$\gamma =0.9$
• 转移概率： $P(s^{\prime }\mid s,a)$：在状态 $s$ 执行动作 $a$ 后转移到 $s^{\prime }$ 的概率；

注意：这是一个典型的 $MDP$（马尔可夫决策过程），每个格子是一个“状态”，每次移动是一个“动作”。

状态值函数$V^{\pi }(s)$

$$V^{\pi }(s)={\mathbb{E}}_{\pi }\left[\sum _{t=0}^{\infty }{\gamma }^{t}R(s_t,a_t)\mid s_0=s\right]$$
表示从状态 $s$ 开始，按照策略 $\pi$ 行动，未来所有折扣回报的期望。是一个状态到回报值的映射
1. 策略设定
首先假设一种策略$\pi$，看在这种策略设定下，状态值函数$V$的值是多少。假设策略是“总是向右走，直到不能走，然后向下”，比如：

• 在状态$(0,0)$：执行动作向右 → $(0,1)$
• 在状态$(0,1)$：执行动作向右 → $(0,2)$
• … …
• 在状态$(0,4)$：执行动作向下 → $(1,4)$
• 在状态$(1,4)$：执行动作向下 → $(2,4)$
• … …

2. MDP中的随机性分析
MDP允许以下三种随机性来源：

随机性来源	说明
1. 策略随机性	策略 $\pi (a)$，如上面的例子，具体的执行方向符合一定的概率分布
2. 状态转移随机性	动作执行后，下一个状态 $s^{\prime }$ 可能不确定（如打滑）, 比如执行向右后并不一定真的移动到右边格子
3. 奖励随机性	即使在相同 $(s,a,s^{\prime })$ 下，奖励 $R$ 也可能不同（如带噪声）

只要存在任意一种随机性，未来轨迹(参考这里定义的MDP的轨迹，以及同随机过程中的轨迹的区别)就不是唯一的，回报就不是一个固定值，而是一个随机变量。用 期望 来描述“平均能获得多少回报”。

在上述机器人轨迹规划的例子中，如果对上述的随机性做一些限制，则能更明显的说明公式含义，因此，我们有如下简化假设：

• 策略是确定性的：比如在状态$s$执行动作$a$后，就一定能到达$a$，即 $\pi (a|s)=1$ 对某个动作 $a$
• 转移是确定性的：执行动作后，机器人一定到达目标格子（无打滑）
• 奖励是确定性的：每步 $-1$，终点 $+10$
• 上述假设和公式的完整形式仅仅相差一个期望 $E$
• 当基于上述假设时，环境和策略都是确定性的，所以所有可能轨迹只有一条，期望就退化为该轨迹的折扣回报总和。

3. 计算特定状态下的状态值函数的具体数值。计算$s=(0,0)$时的状态值函数$V^{\pi }((0,0))$
依照设定的策略进行行走时，状态变化为：
$$(0,0)\to (0,1)\to (0,2)\to (0,3)\to (0,4)\to (1,4)\to (2,4)\to (3,4)\to (4,4)$$
共 8 步，每步奖励 -1，最后一步 +10（到达终点），依据公式可以求得折扣回报
$$V^{\pi }((0,0))=(-1)\cdot {\gamma }^0+(-1)\cdot {\gamma }^1+\cdots +(-1)\cdot {\gamma }^6+10\cdot {\gamma }^7$$$$=-\sum _{k=0}^6{\gamma }^k+10\cdot {\gamma }^7$$代入 $\gamma =0.9$：

• ${\sum }_{k=0}^{6}0.9^k\approx \frac{1-0.9^7}{1-0.9}\approx \frac{1-0.478}{0.1}=5.22$
• $10\cdot 0.9^7\approx 10\cdot 0.478=4.78$

所以：
$$V^{\pi }((0,0))\approx -5.22+4.78=-0.44$$

4. 每个状态下的值函数
   依据上述公式的计算流程，我们可以计算(0, 0)到(4, 4)每个状态下的状态值函数的具体数值。

i\j	0	1	2	3	4
0	-0.434	0.628	1.810	3.122	4.580
1	0.628	1.810	3.122	4.580	6.200
2	1.810	3.122	4.580	6.200	8.000
3	3.122	4.580	6.200	8.000	10.000
4	4.580	6.200	8.000	10.000	0.000

状态值函数的本质是：在给定策略下，从状态 s 出发，所有可能轨迹的折扣回报的期望

动作值函数 $Q^{\pi }(s,a)$

$$Q^{\pi }(s,a)={\mathbb{E}}_{\pi }\left[\sum _{t=0}^{\infty }{\gamma }^{t}R(s_t,a_t)\mid s_0=s,a_0=a\right]$$
表示从状态 $s$ 开始，首先执行动作 $a$，之后按照策略 $\pi$ 继续行动，所能获得的期望折扣回报

在上述$5X5$网格的例子中，策略和环境均是确定性的，上式等价于：
$$Q^{\pi }(s,a)=R(s,a,s^{\prime })+\gamma V^{\pi }(s^{\prime })$$

• 从状态 $s$ 执行动作 $a$ 后，立即获得的奖励 $R(s,a,s^{\prime })$；
• 加上折扣因子 $\gamma$ 乘以下一状态 $s^{\prime }$ 下的状态值函数 $V^{\pi }(s^{\prime })$，即后续所有期望回报的折现

示例 1：计算 $Q^{\pi }((0,0),\text{Right})$

• 当前状态：$(0,0)$
• 动作：$Right$ → 下一状态：$(0,1)$
• 即时奖励：$R=-1$
• $V^{\pi }((0,1))=0.628$ （由前面的表得出）
• $\gamma =0.9$
  $$Q^{\pi }((0,0),\text{Right})=(-1)+0.9\cdot 0.628=-1+0.5652=\boxed{-0.4348}$$

示例 2：计算 $Q^{\pi }((0,0),\text{Down})$

• 当前状态：$(0,0)$
• 动作：$Down$ → 下一状态：$(1,0)$
• $V^{\pi }((1,0))=0.628$
• $R=-1$
  $$Q^{\pi }((0,0),\text{Down})=(-1)+0.9\cdot 0.628=-1+0.5652=\boxed{-0.4348}$$

示例 3：计算 $Q^{\pi }((0,0),\text{Up})$

• 当前状态：$(0,0)$
• 动作 Up：越界 → 无法移动 → 仍停留在 $(0,0)$
• 即时奖励：$-1$
• 下一状态：$(0,0)$
• $V^{\pi }((0,0))=-0.434$
  $$Q^{\pi }((0,0),\text{Up})=(-1)+0.9\cdot (-0.434)=-1-0.3906=\boxed{-1.3906}$$

❌ 这个动作明显更差！

二者比较

1. 状态值函数 $V^{\pi }(s)$:

   • “我现在在状态 $s$，我按照策略 $\pi$ 走下去，平均能得多少分？”
   • 评价“这个状态有多好”。

2. 动作值函数 $Q^{\pi }(s,a)$:

   • “我现在在状态 $s$，如果我先做动作 $a$，然后继续按策略走，平均能得多少分？”
   • 评价“这个动作在当前状态下的好坏”。

不同点	状态值函数 $V^{\pi }(s)$	动作值函数 $Q^{\pi }(s,a)$
🚀 输入参数	只依赖于状态 $s$	依赖于状态 $s$ 和动作 $a$
🎯 用途	评估“处于某个状态”的价值	评估“在某个状态执行某个动作”的价值
💡 决策依据	不能直接指导动作选择，需结合策略	可直接用于动作选择（如 $\arg {\max }_{a}Q(s,a)$）
🤝 与策略的关系	$V^{\pi }(s)={\sum }_a\pi (a\mid s)Q^{\pi }(s,a)$	$Q^{\pi }(s,a)$
⚙️ 计算方式	通过对动作取期望得到：$V^{\pi }(s)={\sum }_a\pi (a\mid s)Q^{\pi }(s,a)$	$Q^{\pi }(s,a)$
🏆 最优性表达	最优状态值函数：$V^{\ast }(s)={\max }_{\pi }{V}^{\pi }(s)$	最优动作值函数：$Q^{\ast }(s,a)={\max }_{\pi }{Q}^{\pi }(s,a)$，且可以直接用于最优策略提取

贝尔曼函数

贝尔曼方程（$BellmanEquation$）是强化学习（$ReinforcementLearning,RL$）中的核心概念，用于描述值函数（$valuefunction$）的递归结构。它将当前状态（或状态-动作对）的价值与其后续状态（或动作）的价值联系起来，体现了动态规划中最优子结构（$optimalsubstructure$）的思想。

动态规划的两个核心特征：重叠子问题和最优子结构
如果对动态规划不太熟悉，强烈建议详细观看教程：

1. 递归的思想
2. 动态规划的思想
3. 动态规划的具体例子

在强化学习中，有两个关键的贝尔曼方程：贝尔曼期望方程和贝尔曼最优方程。

贝尔曼期望函数(Bellman Expectation Equation)

这是针对给定策略（policy）下的值函数的递归关系，用于评估一个策略的好坏。

状态值函数 ($State-valuefunction$) 的贝尔曼期望方程

状态值函数 $V^{\pi }(s)$ 表示在策略 $\pi$ 下，从状态 $s$ 开始，未来累积回报的期望值。
其贝尔曼期望方程为：
$$V^{\pi }(s)=\sum _a\pi (a|s)\sum _{s^{\prime },r}p(s^{\prime },r|s,a)\left[r+\gamma V^{\pi }(s^{\prime })\right]$$

• $\pi (a|s)$: 策略 $\pi$ 在状态 $s$ 下选择动作 $a$ 的概率；
• $p(s^{\prime },r|s,a)$: 环境的动态模型，即在状态 $s$ 执行动作 $a$ 后，转移到状态 $s^{\prime }$ 并获得奖励 $r$ 的概率；
• $\gamma$: 折扣因子（$0\le \gamma \le 1$）

动作值函数 ($Action-valuefunction$) 的贝尔曼期望方程

动作值函数 $Q^{\pi }(s,a)$ 表示在策略 $\pi$ 下，从状态 $s$ 执行动作 $a$ 后，未来累积回报的期望值。
其贝尔曼期望方程为：
$$Q^{\pi }(s,a)=\sum _{s^{\prime },r}p(s^{\prime },r|s,a)\left[r+\gamma \sum _{a^{\prime }}\pi (a^{\prime }|s^{\prime })Q^{\pi }(s^{\prime },a^{\prime })\right]$$
或等价地：
$$Q^{\pi }(s,a)=\sum _{s^{\prime },r}p(s^{\prime },r|s,a)\left[r+\gamma V^{\pi }(s^{\prime })\right]$$

• $Q^{\pi }(s,a)$: 在策略 $\pi$ 下，在状态 $s$ 情况下，执行动作 $a$ 的期望回报；
• $p(s^{\prime },r|s,a)$: 状态转移与奖励的概率分布；
• $\gamma$: 折扣因子；
• $\pi (a^{\prime }|s^{\prime })$: 在新状态 $s^{\prime }$ 下选择动作 $a^{\prime }$ 的概率

---

贝尔曼最优函数 ($BellmanOptimalityEquation$)

贝尔曼最优方程描述的是最优策略（$optimalpolicy$）下的值函数，即所有策略中能达到的最大值。

最优状态值函数 ($OptimalState-valueFunction$)

$$V^{\ast }(s)=\underset{a}{\max }\sum _{s^{\prime },r}p(s^{\prime },r|s,a)\left[r+\gamma V^{\ast }(s^{\prime })\right]$$

最优动作值函数 ($OptimalAction-valueFunction$)

$$Q^{\ast }(s,a)=\sum _{s^{\prime },r}p(s^{\prime },r|s,a)\left[r+\gamma \underset{a^{\prime }}{\max }{Q}^{\ast }(s^{\prime },a^{\prime })\right]$$这些方程不依赖于某个具体策略，而是直接寻找最优动作，体现了最优控制的思想。

关系

与状态值函数、动作值函数的关系总结

概念	定义	对应贝尔曼方程
状态值函数 $V^{\pi }(s)$	策略 $\pi$ 下从状态 $s$ 开始的期望回报	贝尔曼期望方程 (for $V^{\pi }$)
动作值函数 $Q^{\pi }(s,a)$	策略 $\pi$ 下在 $s$ 采取 $a$ 后的期望回报	贝尔曼期望方程 (for $Q^{\pi }$)
最优状态值函数 $V^{\ast }(s)$	所有策略中从 $s$ 开始的最大期望回报	贝尔曼最优方程 (for $V^{\ast }$)
最优动作值函数 $Q^{\ast }(s,a)$	所有策略中在 $s$ 采取 $a$ 后的最大期望回报	贝尔曼最优方程 (for $Q^{\ast }$)

• 贝尔曼期望方程：告诉我们“如果我按某个策略走，现在在这个状态/动作值多少”。
• 贝尔曼最优方程：告诉我们“如果我总是做最好的选择，现在在这个状态/动作最多能值多少”。

它们是动态规划、价值迭代、策略迭代、Q-learning、SARSA 等算法的理论基础。

---

如何求解贝尔曼最优函数

继续基于前面的内容，深入讲解如何求解贝尔曼最优方程。在环境模型（即状态转移概率 $p(s^{\prime },r|s,a)$）和奖励函数已知的前提下，我们可以使用动态规划（Dynamic Programming, DP）方法来求解最优策略。

动态规划是强化学习中用于规划（planning）的一类经典方法，它依赖于完全已知的环境模型，通过迭代更新值函数来逼近最优解。

值迭代与策略迭代：理论部分

1. 共同前提

• 环境是有限马尔可夫决策过程（Finite MDP）；
• 状态空间 $\mathcal{S}$、动作空间 $\mathcal{A}$ 有限；
• 转移概率 $p(s^{\prime },r|s,a)$ 和奖励函数 $r(s,a,s^{\prime })$ 已知；
• 折扣因子 $\gamma \in [0,1)$（通常取 0.9 或 0.99）。

目标：求出最优状态值函数 $V^{\ast }(s)$ 或最优动作值函数 $Q^{\ast }(s,a)$，从而导出最优策略 $\pi$

2. 值迭代

核心思想：直接对贝尔曼最优方程进行迭代逼近，不显式维护策略。
算法步骤：

• 初始化：对所有状态 $s$，设 $V_0(s)=0$（或其他任意值）。

• 迭代更新（对每个 $k=0,1,2,\dots$）：
  $$V_{k+1}(s)\leftarrow \underset{a}{\max }\sum _{s^{\prime },r}p(s^{\prime },r|s,a)\left[r+\gamma V_k(s^{\prime })\right],\forall s\in \mathcal{S}$$

• 重复直到收敛（即 $\Vert V_{k+1}-V_k{\Vert }_{\infty }<ϵ$）。

• 最优策略由最终的 $V^{\ast }$ 导出：
  $${\pi }^{\ast }(s)=\arg \underset{a}{\max }\sum _{s^{\prime },r}p(s^{\prime },r|s,a)\left[r+\gamma V^{\ast }(s^{\prime })\right]$$

• 特点：

  • 每次迭代都“贪心地”选择当前最优动作；
  • 收敛速度快（理论上以几何速率收敛）；
  • 不需要显式策略，但最后一步需提取策略。

3. 策略迭代

核心思想：交替进行 策略评估（Policy Evaluation）和 策略改进（Policy Improvement），直到策略不再变化。

算法步骤：

1. 初始化：任意策略 ${\pi }_0$

2. 重复以下两步直到收敛：

   • 策略评估：给定当前策略 $\pi$，求解其状态值函数 $V^{\pi }(s)$，即解贝尔曼期望方程：
     $$V^{\pi }(s)=\sum _a\pi (a|s)\sum _{s^{\prime },r}p(s^{\prime },r|s,a)\left[r+\gamma V^{\pi }(s^{\prime })\right]$$
     通常通过迭代（类似值迭代但固定策略）或直接解线性方程组实现。
   • 策略改进：
     基于当前 $V^{\pi }$，构造一个更优（或相等）的确定性策略：
     $${\pi }_{\text{new}}(s)=\arg \underset{a}{\max }\sum _{s^{\prime },r}p(s^{\prime },r|s,a)\left[r+\gamma V^{\pi }(s^{\prime })\right]$$

3. 终止条件：当 ${\pi }_{\text{new}}=\pi$ 时，$\pi$ 即为最优策略 ${\pi }^{\ast }$

4. 特点：

   • 每次策略改进都严格提升（或保持）性能；
   • 通常比值迭代迭代次数少，但每次迭代计算量更大（需完整策略评估）；
   • 保证在有限步内收敛到最优策略。

---

值迭代与策略迭代：案例实践

问题定义回顾

• 网格大小：$5\times 5$，状态坐标为 $(i,j)$，其中 i,j∈{0,1,2,3,4}i, j \in \{0, 1, 2, 3, 4\}i,j∈{0,1,2,3,4}

• 起点：$(0,0)$，终点（目标状态）：$(4,4)$

• 动作空间：A={up,down,left,right}A = \{\text{up}, \text{down}, \text{left}, \text{right}\}A={up,down,left,right}

• 环境动态：状态转移是确定性的

  • 执行动作后，若新位置在网格内，则移动；
  • 若出界（如从 $(0,0)$ 向上或向左），则停留在原地。

• 奖励函数：

  • 每执行一个动作（无论是否移动）：立即奖励 = -1
  • 仅当到达 $(4,4)$ 时：该步奖励为 +10（注意：是在进入 $(4,4)$ 的那一步获得 +10）
  • 一旦到达 $(4,4)$，过程终止（后续无动作，无奖励）

• 折扣因子：$\gamma =0.9$

---

值迭代(及python实现)

0. 目标：通过值迭代求解最优状态值函数 $V^{\ast }(s)$
1. 奖励公式：奖励是在执行动作后、转移到新状态时获得的。因此，从状态 $s$ 执行动作 $a$ 转移到 $s^{\prime }$，获得的奖励为：
   $$r=\{\begin{array}{ll}10,& \text{if }{s}^{\prime }=(4,4)\\ -1,& \text{otherwise}\end{array}$$
2. 值迭代公式（确定性环境简化）。由于环境是确定性的，转移概率退化为：
   $$s^{\prime }=\text{next}(s,a)$$
   所以贝尔曼最优方程简化为：
   $$V_{k+1}(s)=\underset{a\in A}{\max }\left[r(s,a)+\gamma V_k(s^{\prime })\right]$$其中：
   • $s^{\prime }=\text{next}(s,a)$
   • $r(s,a)=\{\begin{array}{ll}10,& \text{if }{s}^{\prime }=(4,4)\\ -1,& \text{otherwise}\end{array}$
3. 计算步骤

• 🔷 步骤 1：初始化 $V_0(s)$。通常初始化为全 0（也可任意）：
  $$V_0(s)=0\text{for all }s\in \text{grid}$$
  特别地，终点 $(4,4)$ 是终止状态，我们约定：
  $$V_k((4,4))=0\text{for all }k$$

i\j	0	1	2	3	4
0	0	0	0	0	0
1	0	0	0	0	0
2	0	0	0	0	0
3	0	0	0	0	0
4	0	0	0	0	0

这里的$V_0(s)$是一个函数，是从状态$s=(i,j)$到值$V$的映射。
角标$0$表示 $k=0$ 次迭代

• 🔷 步骤 2：第一次迭代 —— 计算 $V_1(s)$
  我们要对每个非终点状态 $s\ne (4,4)$ 计算：
  $$V_1(s)=\underset{a}{\max }\left[r(s,a)+\gamma \cdot V_0(s^{\prime })\right]=\underset{a}{\max }\left[r(s,a)+0.9\cdot 0\right]=\underset{a}{\max }r(s,a)$$因为 $V_0(s^{\prime })=0$ 对所有 $s^{\prime }$，所以 $V_1(s)$ 就等于从 $s$ 出发能获得的最大即时奖励， 当某个动作 $a$ 能让智能体直接进入 $(4,4)$ 时，$r(s,a)=10$，否则，所有动作的奖励都是 -1
  显然，只有两个邻居能一步到达 $(4,4)$：
  • 从 $(3,4)$ 向下 → $(4,4)$
  • 从 $(4,3)$ 向右 → $(4,4)$
    所以：
  • $V_1(3,4)={\max }_{a}r=10$（选择 “$down$”）
  • $V_1(4,3)={\max }_{a}r=10$（选择 “$right$”）
    其他所有状态，无论怎么走，都无法在一步内到达 $(4,4)$，所以它们的所有动作奖励都是 $-1$，因此：对于这些状态，$V_1(s)={\max }_{a}r(s,a)=-1$

i\j	0	1	2	3	4
0	-1	-1	-1	-1	-1
1	-1	-1	-1	-1	-1
2	-1	-1	-1	-1	-1
3	-1	-1	-1	-1	10
4	-1	-1	-1	10	0

• 🔷 步骤 3：第二次迭代 —— 计算 $V_2(s)$
  逐类分析状态

  • 🟢 类型 1: 终点 (4,4) 保持: $V_2(4,4)=0$

  • 🟢 类型 2: 能一步到终点的状态（$V_1$ 中为 10）

  • 对于状态(3,4): 向下 → (4,4), 奖励 = 10, 但注意：一旦到达 (4,4), 过程终止，所以：
    $$V_2(3,4)=10+0.9\cdot V_1(4,4)=10+0=10$$其他动作（如向上到 $(2,4)$）：$奖励=-1+0.9\times (-1)=-1.9$ ，所以仍选向下，$V_2(3,4)=10$

  • 对于状态(4,3): 同理，$V_2(4,3)=10$

  • 🟢 类型 3: 能一步到达“值为 10”的状态（即离终点两步）
    这些状态的邻居包含 (3,4) 或 (4,3)，所以可以间接获得高价值。

  • 状态(2,4):

    • down → (3,4), $s^{\prime }=(3,4)$，不是终点 → 奖励 = -1
      $$V_2=-1+0.9\cdot V_1(3,4)=-1+0.9\times 10=-1+9=8$$
    • 其他动作（up→(1,4), left→(2,3)）：$V_1=-1$ →
      $$V_2=-1+0.9\times (-1)=-1.9$$
    • 最大值：$V_2(2,4)=8$

  • 状态(3,3): 同理 $V_2(3,3)=8$

  • 🟢 类型 4: 其他不能能一步到达“值为 10”的状态，如 (3,2), (2,3) 等（即离终点大于两步）

    • 它们的邻居在 $V_1$ 中都是 -1，所以最大 $V_2=-1+0.9\times (-1)=-1.9$

i\j	0	1	2	3	4
0	-1.9	-1.9	-1.9	-1.9	-1.9
1	-1.9	-1.9	-1.9	-1.9	-1.9
2	-1.9	-1.9	-1.9	-1.9	8
3	-1.9	-1.0	-1.9	8	10
4	-1.9	-1.9	8	10	0

3. python代码实现
   基本实现

import numpy as np
import matplotlib.pyplot as plt# ----------------------------
# 环境参数
# ----------------------------
GRID_SIZE = 5
GOAL = (4, 4)
ACTIONS = ['up', 'down', 'left', 'right']
GAMMA = 0.9
REWARD_STEP = -1
REWARD_GOAL = 10
THRESHOLD = 1e-4  # 收敛阈值# ----------------------------
# 辅助函数：执行动作
# ----------------------------
def step(state, action):i, j = stateif action == 'up':i = max(0, i - 1)elif action == 'down':i = min(GRID_SIZE - 1, i + 1)elif action == 'left':j = max(0, j - 1)elif action == 'right':j = min(GRID_SIZE - 1, j + 1)next_state = (i, j)# 奖励：只有进入 GOAL 时为 +10，否则 -1reward = REWARD_GOAL if next_state == GOAL else REWARD_STEPreturn next_state, reward# ----------------------------
# 值迭代主函数
# ----------------------------
def value_iteration():# 初始化值函数V = np.zeros((GRID_SIZE, GRID_SIZE))V[GOAL] = 0  # 终止状态值为0（虽然后续不会更新它）iteration = 0while True:delta = 0V_old = V.copy()for i in range(GRID_SIZE):for j in range(GRID_SIZE):if (i, j) == GOAL:continue  # 跳过终点v = V_old[i, j]# 计算所有动作的 Q 值q_values = []for a in ACTIONS:next_state, reward = step((i, j), a)ni, nj = next_stateq = reward + GAMMA * V_old[ni, nj]q_values.append(q)V[i, j] = max(q_values)delta = max(delta, abs(v - V[i, j]))iteration += 1print(f"Iteration {iteration}, max delta: {delta:.6f}")if delta < THRESHOLD:breakreturn V, iteration# ----------------------------
# 从 V 提取最优策略
# ----------------------------
def extract_policy(V):policy = np.empty((GRID_SIZE, GRID_SIZE), dtype='<U5')for i in range(GRID_SIZE):for j in range(GRID_SIZE):if (i, j) == GOAL:policy[i, j] = 'G'continueq_values = []for a in ACTIONS:next_state, reward = step((i, j), a)ni, nj = next_stateq = reward + GAMMA * V[ni, nj]q_values.append(q)best_action = ACTIONS[np.argmax(q_values)]policy[i, j] = best_actionreturn policy# ----------------------------
# 可视化函数
# ----------------------------
def plot_value_function(V, title="Value Function"):plt.figure(figsize=(6, 5))im = plt.imshow(V, cmap='viridis', origin='lower')plt.colorbar(im)plt.title(title)plt.xlabel('Column (j)')plt.ylabel('Row (i)')# 标注数值for i in range(GRID_SIZE):for j in range(GRID_SIZE):plt.text(j, i, f'{V[i, j]:.1f}', ha='center', va='center', color='white', fontsize=9)plt.show()def plot_policy(policy, V):plt.figure(figsize=(6, 5))plt.imshow(V, cmap='viridis', origin='lower')plt.colorbar()plt.title("Optimal Policy (Arrows) over Value Function")# 箭头方向映射arrow_map = {'up': (0, -0.3),'down': (0, 0.3),'left': (-0.3, 0),'right': (0.3, 0),'G': (0, 0)}for i in range(GRID_SIZE):for j in range(GRID_SIZE):if policy[i, j] == 'G':plt.text(j, i, 'G', ha='center', va='center', color='red', fontsize=12)else:dx, dy = arrow_map[policy[i, j]]plt.arrow(j, i, dx, dy, head_width=0.1, head_length=0.1, fc='white', ec='white')plt.xlabel('Column (j)')plt.ylabel('Row (i)')plt.show()# ----------------------------
# 主程序
# ----------------------------
if __name__ == "__main__":print("Running Value Iteration on 5x5 Grid...")V, n_iter = value_iteration()print(f"\nConverged in {n_iter} iterations.")# 打印最终值函数print("\nFinal Value Function V*:")print(np.round(V, 2))# 提取并可视化策略policy = extract_policy(V)print("\nOptimal Policy (U=up, D=down, L=left, R=right, G=goal):")policy_symbols = {'up': 'U', 'down': 'D', 'left': 'L', 'right': 'R', 'G': 'G'}policy_display = np.vectorize(policy_symbols.get)(policy)for row in policy_display:print(" ".join(row))# 可视化plot_value_function(V, "Optimal Value Function V*")plot_policy(policy, V)

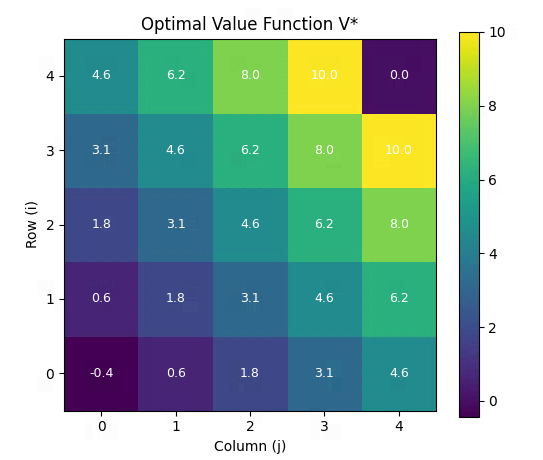
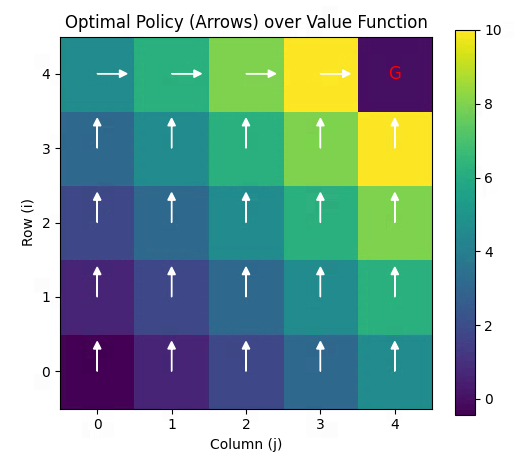
增加障碍物，并且状态空间增大到10*10

import numpy as np
import matplotlib.pyplot as plt# ----------------------------
# 环境参数
# ----------------------------
GRID_SIZE = 10
START = (0, 0)
GOAL = (4, 4)
# 定义障碍物坐标（可任意修改）
OBSTACLES = [(2, 8), (3, 4), (3, 5), (7,2)]  # 示例：三个障碍物ACTIONS = ['up', 'down', 'left', 'right']
GAMMA = 0.9
REWARD_STEP = -1
REWARD_GOAL = 10
THRESHOLD = 1e-4# 转换障碍物为集合，便于快速查询
OBSTACLE_SET = set(OBSTACLES)# 检查是否为有效状态（非障碍物且在网格内）
def is_valid(state):i, j = stateif not (0 <= i < GRID_SIZE and 0 <= j < GRID_SIZE):return Falseif state in OBSTACLE_SET:return Falsereturn True# ----------------------------
# 辅助函数：执行动作（考虑障碍物）
# ----------------------------
def step(state, action):i, j = state# 先计算候选下一位置if action == 'up':ni, nj = i - 1, jelif action == 'down':ni, nj = i + 1, jelif action == 'left':ni, nj = i, j - 1elif action == 'right':ni, nj = i, j + 1else:raise ValueError("Invalid action")# 如果新位置无效（出界或障碍物），则停留在原地if not is_valid((ni, nj)):ni, nj = i, j  # stay in placenext_state = (ni, nj)# 奖励：只有进入 GOAL 时为 +10，否则 -1# 注意：如果 next_state 是障碍物？不会发生，因为已处理reward = REWARD_GOAL if next_state == GOAL else REWARD_STEPreturn next_state, reward# ----------------------------
# 值迭代主函数
# ----------------------------
def value_iteration():V = np.zeros((GRID_SIZE, GRID_SIZE))# 初始化：障碍物和终点特殊处理for i in range(GRID_SIZE):for j in range(GRID_SIZE):if (i, j) == GOAL:V[i, j] = 0  # 终止状态elif (i, j) in OBSTACLE_SET:V[i, j] = 0  # 障碍物值设为0（不参与决策）iteration = 0while True:delta = 0V_old = V.copy()for i in range(GRID_SIZE):for j in range(GRID_SIZE):state = (i, j)# 跳过终点和障碍物if state == GOAL or state in OBSTACLE_SET:continuev = V_old[i, j]q_values = []for a in ACTIONS:next_state, reward = step(state, a)ni, nj = next_stateq = reward + GAMMA * V_old[ni, nj]q_values.append(q)V[i, j] = max(q_values)delta = max(delta, abs(v - V[i, j]))iteration += 1if iteration % 10 == 0 or delta < THRESHOLD:print(f"Iteration {iteration}, max delta: {delta:.6f}")if delta < THRESHOLD:breakreturn V, iteration# ----------------------------
# 提取最优策略
# ----------------------------
def extract_policy(V):policy = np.full((GRID_SIZE, GRID_SIZE), '', dtype='<U5')for i in range(GRID_SIZE):for j in range(GRID_SIZE):state = (i, j)if state == GOAL:policy[i, j] = 'G'elif state in OBSTACLE_SET:policy[i, j] = 'X'else:q_values = []for a in ACTIONS:next_state, reward = step(state, a)ni, nj = next_stateq = reward + GAMMA * V[ni, nj]q_values.append(q)best_action = ACTIONS[np.argmax(q_values)]policy[i, j] = best_actionreturn policy# ----------------------------
# 可视化函数
# ----------------------------
def plot_value_function(V):# 创建掩码：障碍物区域设为 NaN，不显示颜色V_plot = V.astype(float)for (i, j) in OBSTACLE_SET:V_plot[i, j] = np.nanV_plot[GOAL] = 0  # 终点值为0plt.figure(figsize=(6, 5))im = plt.imshow(V_plot, cmap='viridis', origin='lower')plt.colorbar(im, label='Value')plt.title("Optimal Value Function (Obstacles in gray)")plt.xlabel('Column (j)')plt.ylabel('Row (i)')# 标注数值和障碍物for i in range(GRID_SIZE):for j in range(GRID_SIZE):if (i, j) in OBSTACLE_SET:plt.text(j, i, 'X', ha='center', va='center', color='white', fontsize=12, weight='bold')elif (i, j) == GOAL:plt.text(j, i, 'G', ha='center', va='center', color='red', fontsize=12, weight='bold')else:plt.text(j, i, f'{V[i, j]:.1f}', ha='center', va='center', color='white', fontsize=8)plt.show()def plot_policy(policy, V):V_plot = V.astype(float)for (i, j) in OBSTACLE_SET:V_plot[i, j] = np.nanplt.figure(figsize=(6, 5))plt.imshow(V_plot, cmap='viridis', origin='lower')plt.colorbar(label='Value')plt.title("Optimal Policy with Obstacles")arrow_map = {'up': (0, -0.3),'down': (0, 0.3),'left': (-0.3, 0),'right': (0.3, 0)}for i in range(GRID_SIZE):for j in range(GRID_SIZE):if (i, j) in OBSTACLE_SET:plt.text(j, i, 'X', ha='center', va='center', color='white', fontsize=12, weight='bold')elif policy[i, j] == 'G':plt.text(j, i, 'G', ha='center', va='center', color='red', fontsize=12, weight='bold')elif policy[i, j] in arrow_map:dx, dy = arrow_map[policy[i, j]]plt.arrow(j, i, dx, dy, head_width=0.1, head_length=0.1, fc='white', ec='white')plt.xlabel('Column (j)')plt.ylabel('Row (i)')plt.show()# ----------------------------
# 主程序
# ----------------------------
if __name__ == "__main__":print("5x5 Grid World with Obstacles")print(f"Start: {START}, Goal: {GOAL}")print(f"Obstacles: {OBSTACLES}\n")V, n_iter = value_iteration()print(f"\nConverged in {n_iter} iterations.")policy = extract_policy(V)# 打印策略（文本）symbol_map = {'up': 'U', 'down': 'D', 'left': 'L', 'right': 'R', 'G': 'G', 'X': 'X'}policy_text = np.vectorize(symbol_map.get)(policy)print("\nOptimal Policy (U/D/L/R, G=goal, X=obstacle):")for row in policy_text:print(" ".join(f"{cell:>2}" for cell in row))# 可视化plot_value_function(V)plot_policy(policy, V)

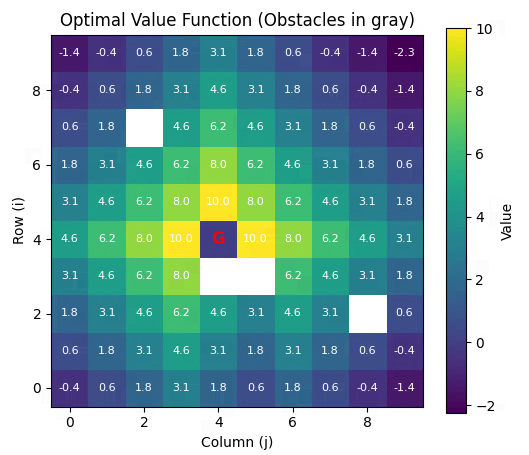
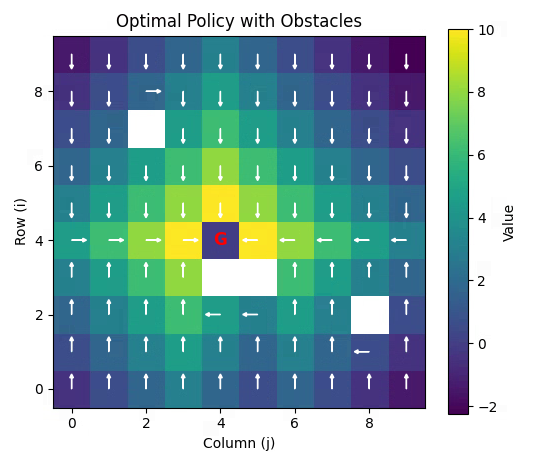
策略迭代(及python实现)

肝不动了, 另起一篇…