Embedding技术:DeepWalkNode2vec
引言
在推荐系统中,Graph Embedding技术已经成为一种强大的工具,用于捕捉用户和物品之间的复杂关系。本文将介绍Graph Embedding的基本概念、原理及其在推荐系统中的应用。
什么是Graph Embedding?
Graph Embedding是一种将图中的节点映射到低维向量空间的技术。通过这种映射,图中的节点可以在向量空间中表示为密集的向量,从而方便进行各种机器学习任务,如分类、聚类和推荐。

Graph Embedding的基本原理
1. 图的表示
一个图 G = ( V , E ) G = (V, E) G=(V,E)由节点集合 V V V和边集合 E E E组成。在推荐系统中,节点可以表示用户或物品,边可以表示用户与物品之间的交互(如点击、购买等)。图可以是有向的或无向的,也可以是加权的(例如,边权重表示交互的强度)。
2. 目标函数
Graph Embedding的目标是学习一个映射函数 f : V → R d f: V \rightarrow \mathbb{R}^d f:V→Rd,将每个节点 v ∈ V v \in V v∈V映射到一个 d d d维的向量空间。这个映射函数通常通过优化以下目标函数来学习:
min f ∑ ( u , v ) ∈ E L ( f ( u ) , f ( v ) ) \min_{f} \sum_{(u, v) \in E} \mathcal{L}(f(u), f(v)) fmin(u,v)∈E∑L(f(u),f(v))
其中, L \mathcal{L} L是损失函数,用于衡量节点 u u u和 v v v在向量空间中的相似性。常见的损失函数包括:
-
负对数似然损失:
L ( f ( u ) , f ( v ) ) = − log σ ( f ( u ) T f ( v ) ) \mathcal{L}(f(u), f(v)) = -\log \sigma(f(u)^T f(v)) L(f(u),f(v))=−logσ(f(u)Tf(v))
其中, σ ( x ) = 1 1 + e − x \sigma(x) = \frac{1}{1 + e^{-x}} σ(x)=1+e−x1是sigmoid函数。 -
欧氏距离损失:
L ( f ( u ) , f ( v ) ) = ∥ f ( u ) − f ( v ) ∥ 2 2 \mathcal{L}(f(u), f(v)) = \|f(u) - f(v)\|_2^2 L(f(u),f(v))=∥f(u)−f(v)∥22
目标函数的核心思想是:如果两个节点在图中是相邻的(即存在边),那么它们在向量空间中的表示应该尽可能相似。
3. 常见的Graph Embedding方法
3.1 DeepWalk
DeepWalk是一种基于随机游走的Graph Embedding方法。它通过在图中进行随机游走,生成节点序列,然后使用Skip-gram模型来学习节点的向量表示。Skip-gram原理可以我前几篇Embedding生成文章

DeepWalk
给定一个起始节点 v i v_i vi,随机游走生成一个节点序列 v i 1 , v i 2 , … , v i k v_{i1}, v_{i2}, \dots, v_{ik} vi1,vi2,…,vik,其中每个节点 v i j v_{ij} vij是从当前节点 v i ( j − 1 ) v_{i(j-1)} vi(j−1)的邻居中随机选择的。(如上图所示)
Skip-gram模型
Skip-gram模型的目标是最大化给定中心节点 v i v_i vi时,其上下文节点 v i − w , … , v i + w v_{i-w}, \dots, v_{i+w} vi−w,…,vi+w的条件概率。目标函数为:
min f − log P ( v i − w , … , v i + w ∣ f ( v i ) ) \min_{f} -\log P(v_{i-w}, \dots, v_{i+w} \mid f(v_i)) fmin−logP(vi−w,…,vi+w∣f(vi))
具体地,Skip-gram模型使用softmax函数来计算条件概率:
P ( v j ∣ v i ) = exp ( f ( v j ) T f ( v i ) ) ∑ v k ∈ V exp ( f ( v k ) T f ( v i ) ) P(v_j \mid v_i) = \frac{\exp(f(v_j)^T f(v_i))}{\sum_{v_k \in V} \exp(f(v_k)^T f(v_i))} P(vj∣vi)=∑vk∈Vexp(f(vk)Tf(vi))exp(f(vj)Tf(vi))
由于直接计算softmax的分母计算量较大,通常采用负采样(Negative Sampling)来近似计算。负采样的目标函数为:
min f − log σ ( f ( v j ) T f ( v i ) ) − ∑ k = 1 K E v k ∼ P n ( v ) log σ ( − f ( v k ) T f ( v i ) ) \min_{f} -\log \sigma(f(v_j)^T f(v_i)) - \sum_{k=1}^K \mathbb{E}_{v_k \sim P_n(v)} \log \sigma(-f(v_k)^T f(v_i)) fmin−logσ(f(vj)Tf(vi))−k=1∑KEvk∼Pn(v)logσ(−f(vk)Tf(vi))
其中, K K K是负采样数, P n ( v ) P_n(v) Pn(v)是负采样分布。
3.2 Node2Vec
Node2Vec是对DeepWalk的改进,它引入了广度优先搜索(BFS)和深度优先搜索(DFS)的策略,可以更好地捕捉图的局部和全局结构。

随机游走策略

Node2Vec的随机游走策略由两个参数控制,以使Embedding结果倾向于同质化(距离相近节点Embedding相似)或结构性(结构上相似节点Embedding应相似):
- 返回参数 p p p:控制游走返回到前一个节点的概率。
- 进出参数 q q q:控制游走远离前一个节点的概率。
具体地,Node2Vec的随机游走概率定义为:
P ( v j ∣ v i ) = { 1 p if d i j = 0 1 if d i j = 1 1 q if d i j = 2 P(v_j \mid v_i) = \begin{cases} \frac{1}{p} & \text{if } d_{ij} = 0 \\ 1 & \text{if } d_{ij} = 1 \\ \frac{1}{q} & \text{if } d_{ij} = 2 \end{cases} P(vj∣vi)=⎩ ⎨ ⎧p11q1if dij=0if dij=1if dij=2
其中, d i j d_{ij} dij是节点 v i v_i vi和 v j v_j vj之间的最短路径距离。
结构性和同质性
在node2vec算法中,通过精心调整p和q参数,可以巧妙地引导节点嵌入(Embedding)的方向,使其呈现出不同的特性。具体而言:
-
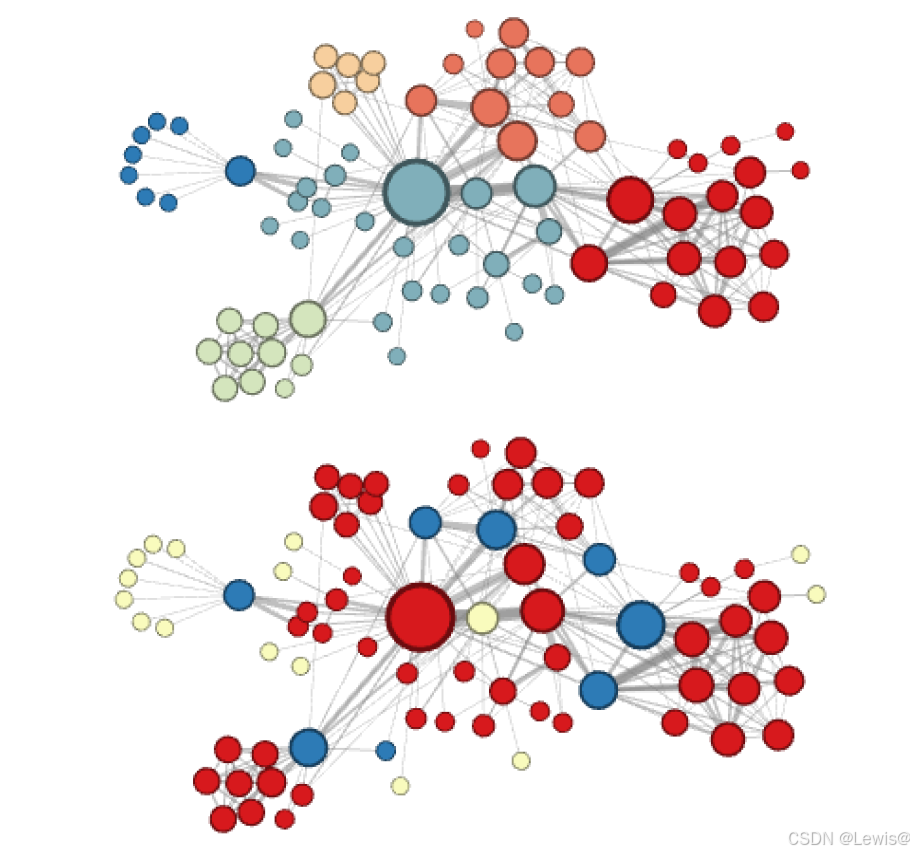
若我们对网络节点的局部特征更为关注,倾向于让相近的节点在嵌入空间中具有相似的表示,那么可通过调整参数使节点Embedding更倾向于同质性,例如上图所示的网络节点Embedding情况;
-
反之,若我们更重视网络的全局结构特征,希望结构相近的节点在嵌入空间中能够彼此靠近,即使它们在实际网络中可能相隔较远,那么就可以像下图那样,使节点Embedding更倾向于结构性。这种灵活的参数调节机制,使得node2vec算法能够根据不同的任务需求和数据特点,生成更符合需求的节点嵌入表示,为后续的图分析和机器学习任务提供了强大的特征支持。
目标函数
Node2Vec的目标函数与DeepWalk类似,但随机游走的策略更加灵活,能够更好地捕捉图的结构信息。目标函数为:
min f − log P ( v i − w , … , v i + w ∣ f ( v i ) ) \min_{f} -\log P(v_{i-w}, \dots, v_{i+w} \mid f(v_i)) fmin−logP(vi−w,…,vi+w∣f(vi))
Graph Embedding在推荐系统中的应用
1. 用户-物品图
在推荐系统中,用户与物品之间的交互行为(如点击、购买、评分等)可以自然地建模为一个用户-物品二分图(User-Item Bipartite Graph)。该图 G = ( V , E ) G = (V, E) G=(V,E) 中,节点集合 V V V 分为两部分:用户节点 U U U 和物品节点 I I I,边集合 E E E 表示用户与物品之间的交互。例如,边 ( u , i ) (u, i) (u,i) 表示用户 u u u 与物品 i i i 的交互行为,边的权重可以表示交互的强度(如点击次数或评分值)。
通过Graph Embedding技术,用户和物品可以被映射到同一个低维向量空间 R d \mathbb{R}^d Rd,从而将复杂的图结构转化为稠密的向量表示。这种表示不仅保留了用户与物品之间的显式交互关系,还能够捕捉隐式的高阶关系(如用户之间的相似性或物品之间的关联性)。
2. 推荐算法
基于Graph Embedding的推荐算法通常包括以下步骤:
-
构建用户-物品图
根据用户与物品的交互数据构建二分图,明确节点和边的定义及其权重。 -
学习用户和物品的向量表示
使用Graph Embedding方法(如DeepWalk、Node2Vec等)将用户和物品映射到低维向量空间,得到向量表示 f ( u ) f(u) f(u) 和 f ( i ) f(i) f(i)。 -
计算相似性并生成推荐列表
对于目标用户 u u u,计算其向量 f ( u ) f(u) f(u) 与所有物品向量 f ( i ) f(i) f(i) 的相似性(如余弦相似度或点积),并根据相似性得分对物品排序,生成个性化推荐列表。
3. 优势
基于Graph Embedding的推荐系统具有以下显著优势:
-
捕捉复杂关系
Graph Embedding能够捕捉用户与物品之间的高阶相似性和隐式反馈。例如,通过随机游走或邻居聚合,可以发现用户之间或物品之间的潜在关联,从而提升推荐的准确性。 -
可扩展性
基于Graph Embedding的方法通常具有较高的可扩展性,能够处理大规模的用户-物品交互数据。例如,GraphSAGE通过邻居采样和聚合机制,降低了计算复杂度,适用于大规模图数据。 -
灵活性
Graph Embedding方法可以与其他推荐技术(如矩阵分解、深度学习等)结合,进一步提升推荐性能。例如,可以将Graph Embedding生成的向量作为输入特征,用于深度学习模型的训练。 -
冷启动问题的缓解
通过捕捉用户与物品之间的高阶关系,Graph Embedding能够为冷启动用户或物品提供更合理的推荐,缓解冷启动问题。
Reference
- 王喆《深度学习推荐系统》
- Perozzi, B., Al-Rfou, R., & Skiena, S. (2014). DeepWalk: Online Learning of Social Representations. Stony Brook University Department of Computer Science.
- Grover, A., & Leskovec, J. (2016). node2vec: Scalable Feature Learning for Networks. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.
