【GNN】第二章:图数据
【GNN】第二章:图数据
图数据和我们平时的看到的数据差别是很大的。先强调一下:图(graph)是图(graph),数据集(dataset)是数据集(dataset), 图是包含在数据集中的。一个数据集中可以只有一个图也可以有多个图。所以我们先讲图graph,然后再讲torch_geometric包中自带的数据集,最后讲如何将我们自己的数据转化为图数据。
一、图论的基本概念
该部分主要介绍图论的基本概念和基本的定义定理,也就是图数据的表示。
1、图的定义1——图中的节点和边的表示
图(Graph)是一种表示对象之间关系的基本结构。具体的,我们用G=(V, E) 来表示图,其中V表示节点Nodes(也叫‘实体entities’) 的集合、E表示边Edges(也叫‘关系’relations) 的集合:
(1)节点和边本身是要embedding成一个特征向量的。这是自然喽,如果不是特征向量,神经网络怎么计算嘛。所以,一个图有三部分特征:
一是,点特征。点是由特征向量来表示的。
二是,边特征。边也是用特征向量来表示的。比如如果要预测两个点之间的关系(朋友关系、亲人关系、同事关系)就是这两个点的边的特征。所以边也是一个向量。
三是,图特征。就是上图的U。图是一个全局的概念。图是由所有的点和所有的边组成的。所以比如所有的点的均值就可以表示图的特征。所有的边的特征的均值就也是图的特征。
(2)一般情况下,节点和边还要有自己的标签:
节点和边的信息可以是类别型的(categorical),类别型数据的取值只能是哪一类别。一般称类别型的信息为标签(label)。
节点和边的信息可以是数值型的(numeric),数值型数据的取值范围为实数。一般称数值型的信息为属性(attribute)。
为什么要有标签?有标签就可以分类或回归了呀。所以,图神经网络是可以完成不同的任务:
比如有的任务是求点的(比如对点进行分类、回归等任务),有的是求边的(比如对边进行分类、回归等任务),有的还是求全局的就是Graph级别的任务(比如设计分子结构等任务)。
为什么“一般情况下”有标签?意思就是可以只有部分标签,就是可以仅仅是一些重要的节点和重要的边才有标签,就是图神经网络可以进行半监督学习的,不是必须所有的节点和边都需要标签的。但是当然还是标签越多越好嘛。
但是无论数据多么随意,我们使用图神经网络的目的就是整合特征,或者说是重构特征。为什么要重构特征?因为每个点都不是孤立的,它都是和一些别的点有联系的,所以一个点的特征的变化是要受到和它有边相连的点的影响的。我们的图神经网络就是拟合(或者说‘捕获’)这种相互之间复杂的作用关系的。
2、图的定义2——图的拓扑结构:邻接矩阵(Adjacency Matrix)、邻接表(Adjacency List)
一个图数据,所有的节点特征、节点标签、边特征、边标签就可以表示一个图数据了嘛?显然是不够的!图的拓扑结构也是有决定作用的:

上面的两个图,它们同样都是有俩黄、俩蓝、俩绿,共6个节点,因此它们的节点信息相同;假如边只表示一种关系,那么它们的边信息也相同。但这两个图显然是不一样的图,因为它们的拓扑结构不一样!所以图的拓扑结构同样也包含了这个图的重要信息,这些拓扑信息后面还要辅助深度学习网络计算节点表征的,就是上面提到的是要辅助“重构特征”的。所以我们还得把图的拓扑结构也用数字表示出来。
如何表示一个图的拓扑结构呢?通常有两种方案:邻接矩阵和邻接表。
邻接矩阵是反映哪两个节点之间有边的矩阵,也是告诉神经网络节点之间的关系的矩阵。邻接矩阵是一个NxN矩阵的形式。
但是有时,当节点非常多的时候,邻接矩阵就会太大,所以有时我们用邻接表来表示一个图的拓扑结构。邻接表是以 (source, target)对儿 的形式存储的,是一种顺序分配和链式分配相结合的存储结构。
(1)所以:NxN邻接矩阵是一个0101的稀疏矩阵;也是一个对称矩阵。
(source,target)对儿的邻接表一个n行2列的矩阵,其中[v1,v2]表示节点v1和节点v2之间是有边的,[v1,v3]表示节点v1和节点v3之间是有边的,其他行同理。
邻接矩阵(邻接表)作为图数据的重要信息,是要作为输入一并传入GNN模型的,GNN在计算节点和边的特征时,邻接矩阵(邻接表)是要参与计算的,具体怎么参与计算,后面讲网络架构原理时会详细展开讲。
(2)上图是一个无向图(Undirected Graph),就是节点v1到节点v2的边存在,就意味着从节点v2到v1的边也是存在的。所以无向图的邻接矩阵是对称的,有向图(Directed Graph)的邻接矩阵是不对称的。
(3)上图还是一个无权图,就是各条边的权重被认为是等价的,即认为各条边的权重都是1。所以如果是一个有权图,那它对应的邻接矩阵Aij=wij,就是从节点vi到vj的边的权重,若边不存在时,边的权重为0。
3、图的属性1——节点的度(Degree)
节点的度就是指一个节点有多少条边和它连接。但是在有权有向图中,边就不仅有方向还有权重,所以一个节点的度(Degree)就被细分为这个节点的出度(out degree)和入度(in degree)。
显然,出度(dout(vi))就是从节点vi出发的边的权重之和;入度(din(vi))就是所有连向节点vi的边的权重之和。
无向图是有向图的特殊情况,所以无向图的节点的出度和入度相等。
无权图又是有权图的特殊情况,无权图的权重为1,所以无权图的节点vi的出度=从vi出发的边的数量,节点vi的入度=所有连向vi的边的数量。
下面是计算一个图的节点的度矩阵(Degree Matrix):

度矩阵也非常非常重要,以后我们讲网络数据传播时,度矩阵也是要和邻接矩阵一样,二者一起要参与节点表征的计算的。
4、图的属性2——邻接节点(neighbors)
与节点vi直接相连的节点,就是节点vi的邻接节点。比如上图的节点A的邻接节点就是E,而节点E的邻接节点是ABCD四个节点。
vi节点k跳远的邻接节点(neighbors with k-hop),指的是到节点vi走k步的节点(一个节点的2跳远的邻接节点包含了自身)。
5、图的属性3——行走(walk)、路径(path)、最短路径(shortest path)
6、图的属性4——子图(subgraph)、连通分量(connected component)、连通图(connected graph)、直径(diameter)
7、图的属性5——拉普拉斯矩阵 (Laplacian Matrix)
说明:上面图论的相关概念仅仅是非常非常少的一部分,也是最常用的一些概念。如果你想知道的更多,可以参考: https://cse.msu.edu/~mayao4/dlg_book/chapters/chapter2.pdf
二、图分析工具:NetworkX
一般我们拿到数据后,都想先可视化一下,直观的了解一下数据,所以这里我先讲一个图论领域常用的工具networkx。
NetworkX是一个图论和网络分析的Python软件包,可以提供丰富的图数据结构和算法,创建、操作和分析各种类型的图。这个工具直接pip install networkx就安装好了。
NetworkX可以创建各种类型的图对象,比如无向图、有向图、有权图等;
NetworkX可以设置节点和边的属性、获取图的邻接矩阵、度、平均度、度分布、度矩阵等;
NetworkX可以进行图分析,因为它内置了很多图论算法,比如图的遍历、最短路径、社区发现、中心性等;
NetworkX可以绘制图对象,支持图数据的可视化,经常用于绘制网络结构。
1、举几个使用例子:


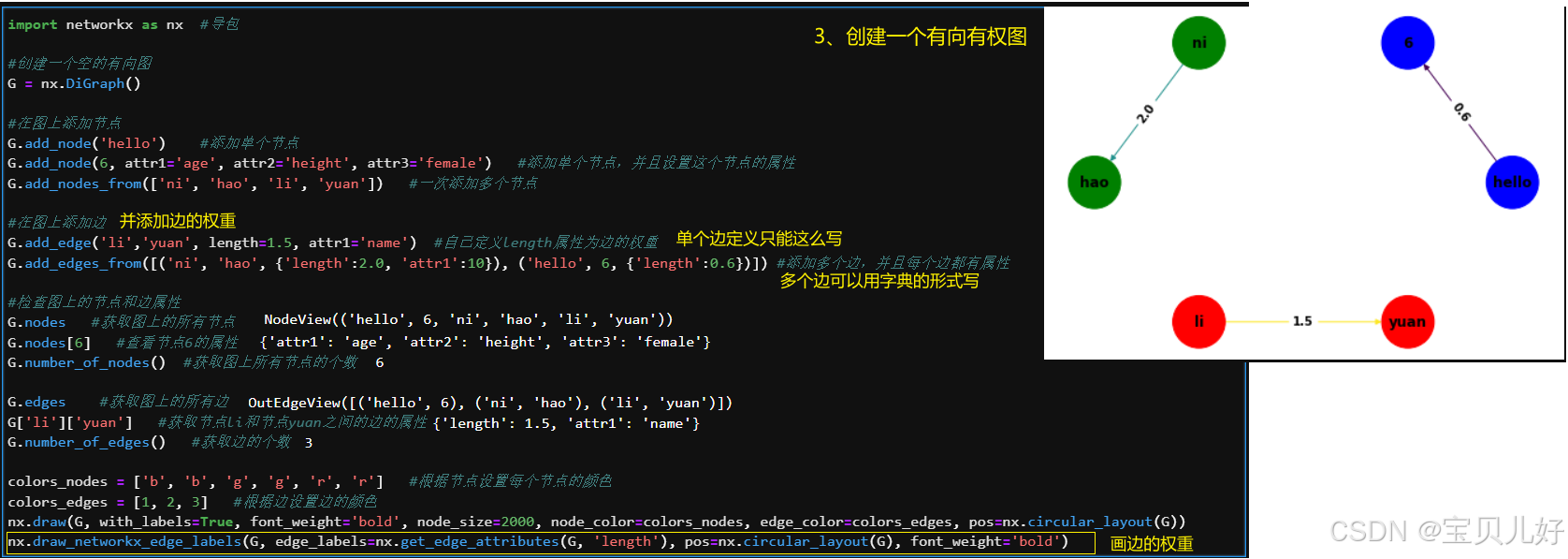

上面只是入门一下这个工具包,其实这个工具包是非常强大的,经常用于复杂网络拓扑结构统计指标计算、典型复杂网络建模(随机图、小世界、无标度等)以及复杂网络可视化的方法等,值得花时间熟悉一下。
2、举一个交通网络优化的小案例:提升城市交通效率的路径优化
假设我们有一个城市的交通网络,由多个路口(节点)和道路(边)组成。我们的目标是从城市的某个起点(比如A点)到达某个终点(比如B点),我们希望:
一是,找到最短路径:从A到B的最短路径。
二是,找到最大流路径:在交通高峰期间,如何最大化从A到B的车辆通过量。
三是,避免拥堵:找到一条尽量避开拥堵区域的路径。


import networkx as nx
# 创建一个有向图来表示交通网络
G = nx.DiGraph()
# 添加节点(路口)
nodes = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H']
G.add_nodes_from(nodes)
# 添加带权重的边(道路)及其通行能力
edges = [('A', 'B', {'weight': 2, 'capacity': 100}), #就是给边设置属性,一个属性是weight,一个属性是capacity
('A', 'C', {'weight': 5, 'capacity': 50}), #weight你可以理解为大家走这条路的“平均用时”
('B', 'C', {'weight': 2, 'capacity': 100}), #capacity你可以理解为这条路的“最大通行量”
('B', 'D', {'weight': 4, 'capacity': 70}),
('C', 'E', {'weight': 1, 'capacity': 120}),
('D', 'F', {'weight': 3, 'capacity': 80}),
('E', 'F', {'weight': 1, 'capacity': 150}),
('F', 'G', {'weight': 2, 'capacity': 90}),
('E', 'H', {'weight': 3, 'capacity': 60}),
('H', 'G', {'weight': 2, 'capacity': 70}),]
G.add_edges_from(edges)
# 可视化交通网络
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei'] #这行代码是用来让图上显示汉字的
plt.figure(figsize=(10, 6)) #搞一个画布
pos=nx.spring_layout(G) #这种模式是随机的,所以别让它运行两次!
nx.draw(G, with_labels=True, node_size=1500, font_size=20, font_weight='bold', pos=pos)
nx.draw_networkx_edge_labels(G, pos=pos, font_size=15,
edge_labels={(i,j): f"w:{k['weight']}, c:{k['capacity']}" for i,j,k in G.edges(data=True)}) #这个参数只接收字典的形式
G.edges(data=True)
plt.title("城市交通网络图") #弄一个标题
plt.show()
#1、基于权重,也就是基于时间,找到从A到G的最短路径
shortest_path = nx.shortest_path(G, source='A', target='G', weight='weight')
shortest_path_length = nx.shortest_path_length(G, source='A', target='G', weight='weight') #这是最短路径用时
shortest_path, shortest_path_length
#2、找到最大流量路径
max_flow_value, max_flow_dict = nx.maximum_flow(G, 'A', 'G',capacity='capacity')
max_flow_value, max_flow_dict
#3、避免拥堵的路径(通过增加某些边的权重来模拟拥堵路径)
# 我们假设边 ('B', 'C') 和 ('E', 'F') 在高峰期很拥堵,因此增加它们的权重
G['B']['C']['weight'] += 10
G['E']['F']['weight'] += 10
# 重新计算最短路径
congestion_avoidance_path = nx.shortest_path(G, source='A', target='G', weight='weight')
congestion_avoidance_path_length = nx.shortest_path_length(G, source='A', target='G', weight='weight')
congestion_avoidance_path, congestion_avoidance_path_length待续。。。。。
