前缀和算法：高效解决区间和问题

目录

理解

例题讲解

牛客网dp34前缀和

牛客网dp35二维前缀和

leetcode724例题

leetcode238例题

leetcode560例题

leetcode974例题

leetcode525例题

leetcode1314例题

总结：

---

理解

前缀和是一种预处理数组的高效算法技巧，核心是通过提前计算数组中 “从起始位置到每个索引位置的元素累加和”，将后续的区间和查询、子数组相关问题从 “暴力遍历的 O (n) 时间” 优化到 “直接查询的 O (1) 时间”，本质是 “空间换时间” 的典型应用。（就是一个小的动态规划，简单的动态规划，想要了解动态规划章节的可以去我的栏目里看）

前缀和解决的问题就是给你一段数组，让求某个区间的和

例题讲解

牛客网dp34前缀和

题目理解：

第一行输入告诉你有几个数，然后几次查询，示例1中有3个数字，2次查询

第二行告诉你这3个数字有什么，这里就是{1，2，4}

第三行开始告诉你查询从哪到哪，（1，2），那就是1+2=3

第四行（2，3），2+4=6

所以输出就是3和6

注意这里下标是从1开始，不是从0，所以我们开辟数组的时候要开辟n+1，让最后一个下标是n

算法原理讲解：

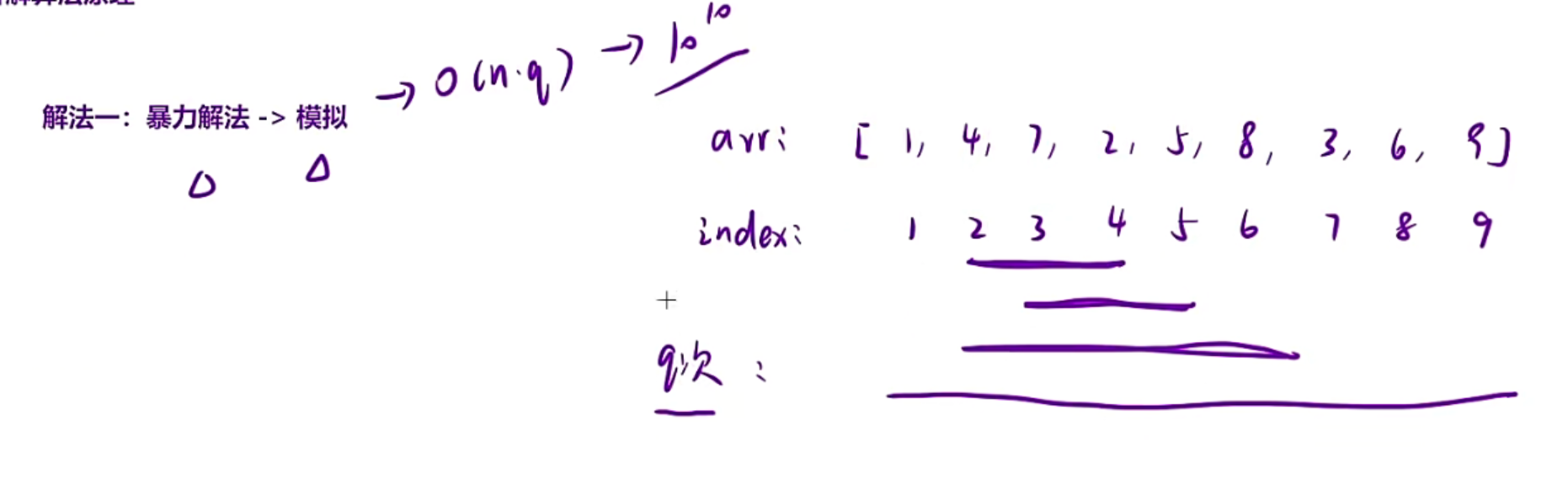
一、暴力解法，你让我算哪个区间我就算哪个区间

时间复杂度O（qN），但是题目当中nq的取值范围一样，如果都是最大，那时间复杂度会变为10^10，如果使用暴力解法这道题是会超时的

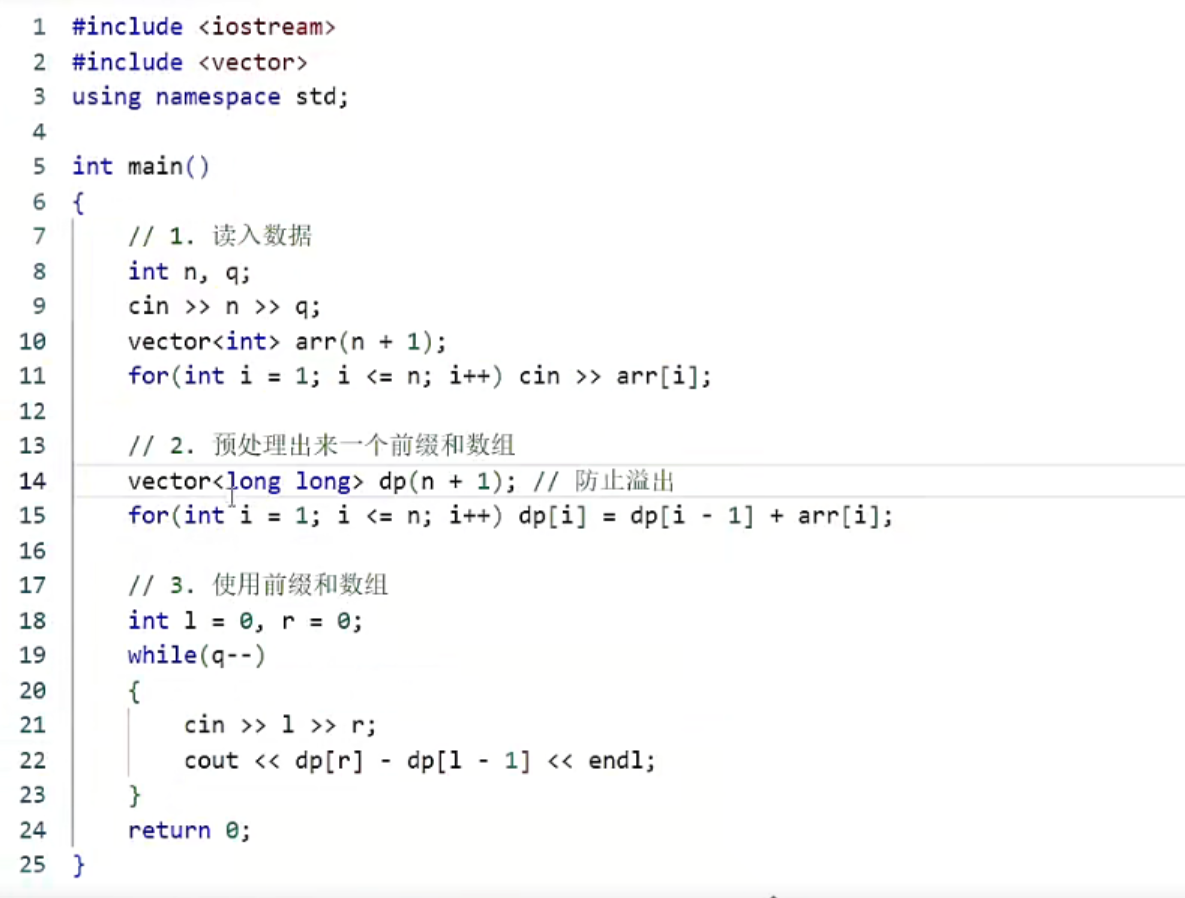
二、前缀和（动态规划）

首先我们要另外开辟一个空间dp，然后dp[i]表示的是【1，i】区间内所有的元素的和

下一个元素的计算是前一个元素+arr[i]

这一次开辟空间填表需要O(N)的时间

然后每次查询需要O(q)

时间复杂度就是O(q)+O(N)

注意：这里为什么可以这样用？是因为你求【3，5】区间和的时候，使用【1，5】-【1，2】

【1，5】的求法和【1，2】的求法一致（本质上是同一类问题），所以我们可以抽象成一个状态表示，使用动态规划

为什么这道题的下标是从1开始计数？

如果下标是0开始，就需要处理一下边界问题

因为你的求解方程是dp[r]-dp[l-1]，你要想一下什么时候会越界？

如果求解的方程是【0，2】，dp[2]-dp[-1]，所以特殊情况要处理一下，那就需要开辟数组的时候从1开始，然后原题对应的数组要统一从下标1开始放，放的时候要跟原数组对应好

牛客网dp35二维前缀和

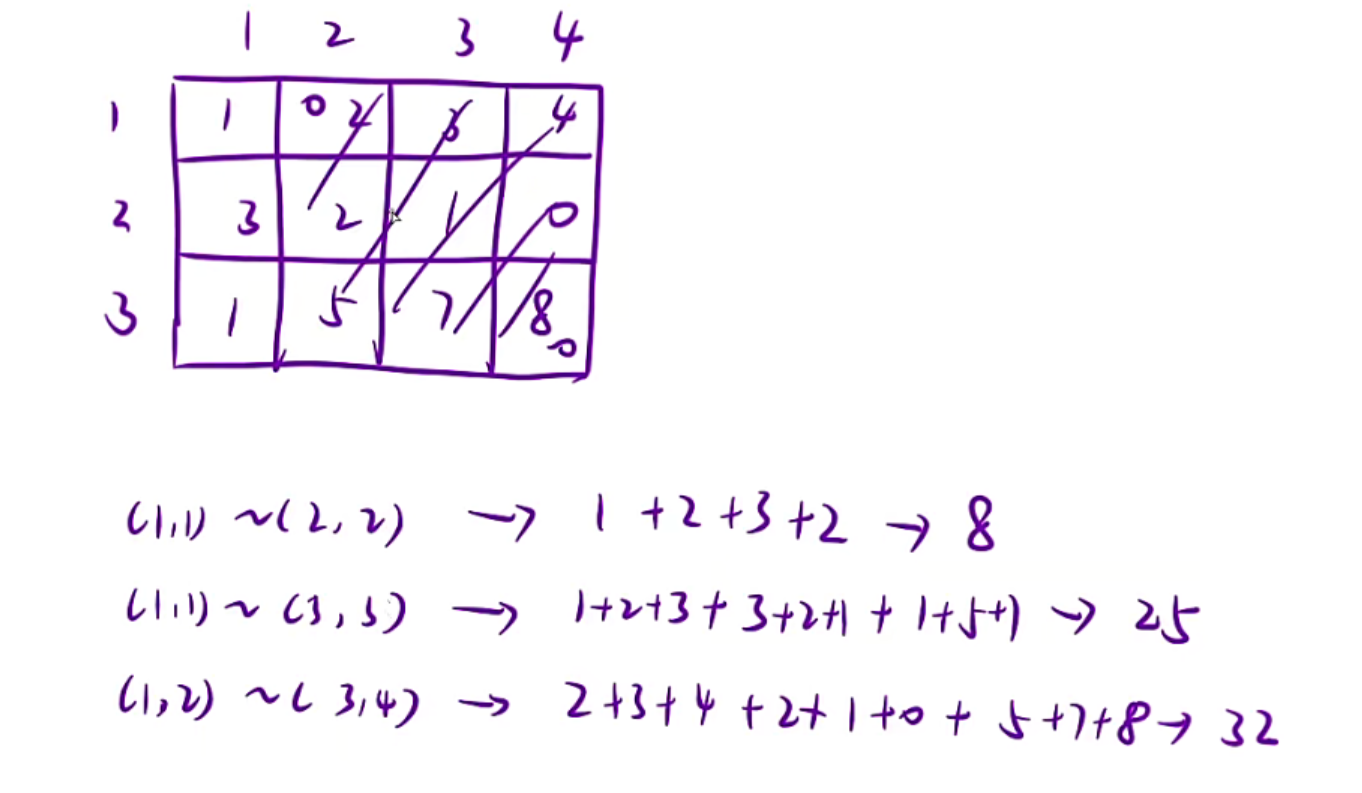
题目讲解：

给一个二维数组，然后给左上角坐标和右下角坐标，求这个矩阵的和

算法原理讲解：

一、暴力解法，时间复杂度O(m*n*q)

二、前缀和

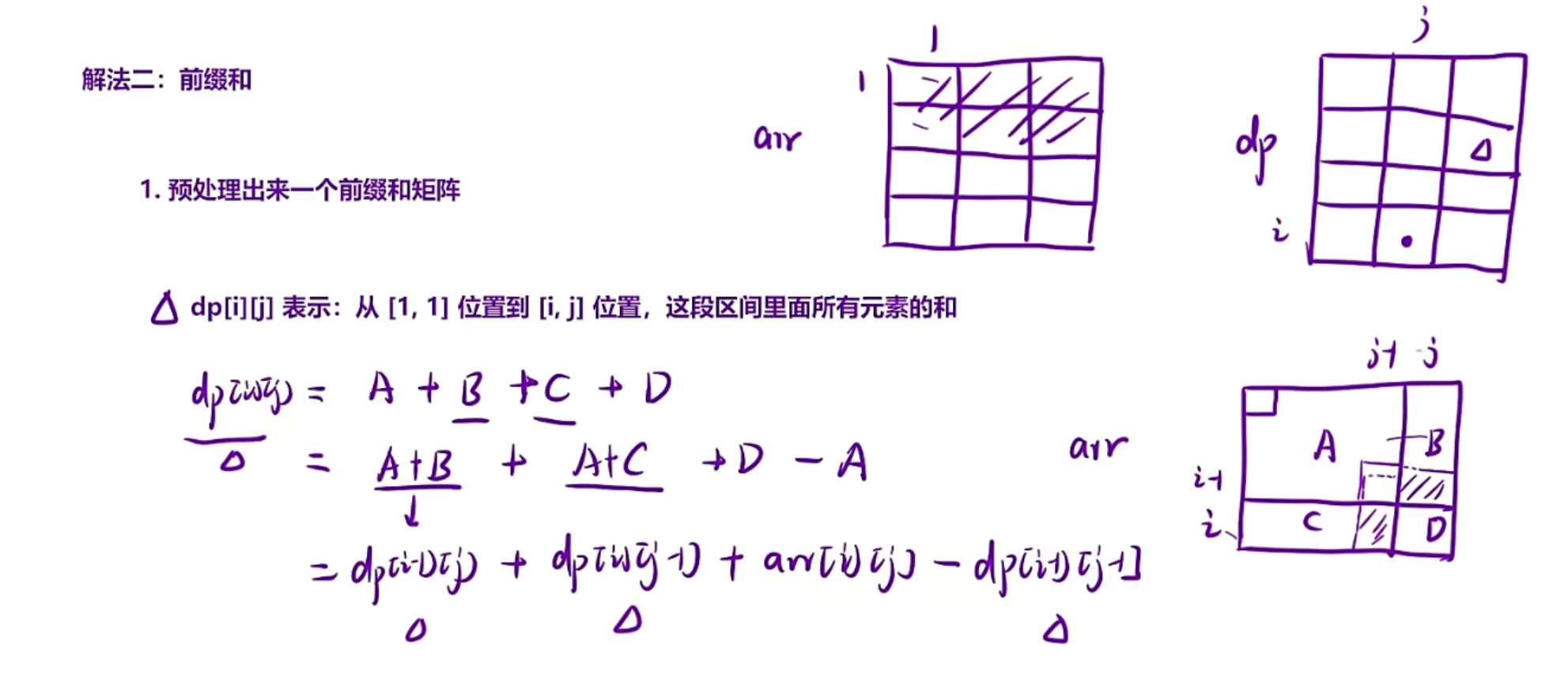
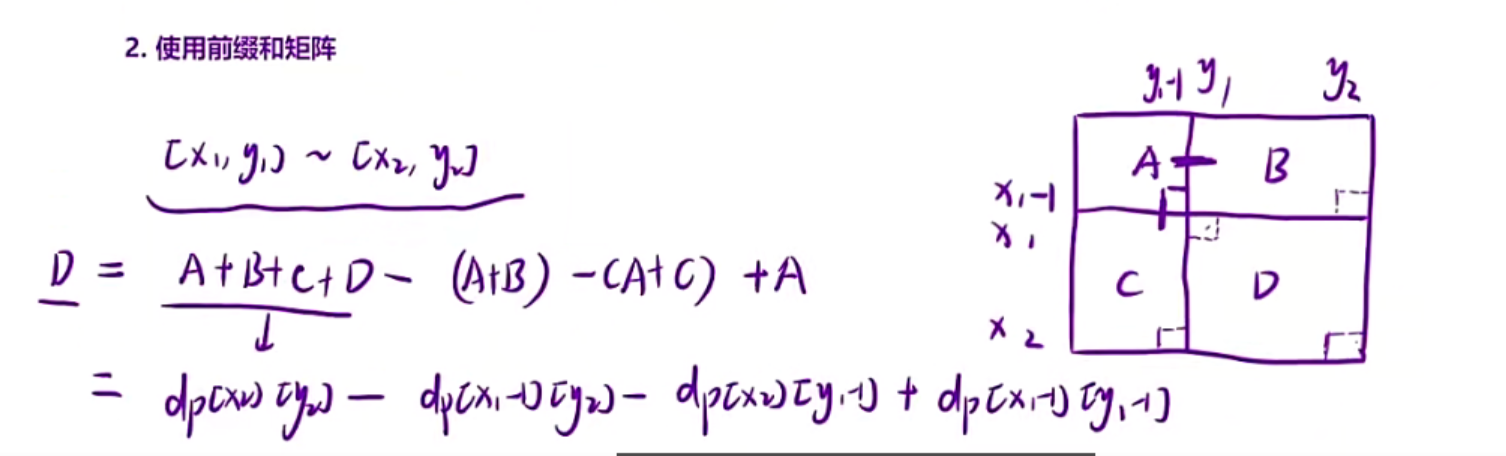
时间复杂度为O（mn）+O（q）

leetcode724例题

算法原理讲解：

前缀和

读题发现就是找到一个中心坐标，使得左边的和=右边的和，那从左边加到中心坐标可以看成一个前缀和，右边加到中心坐标可以看成一个前缀和，那此时只要比对一下，前缀和相等的时候返回即可，如果没有相等即返回-1

所以我们可以创建一个二维数组，第0行就是存从左到中心坐标，第1行就是存从右到中心坐标

但是这里我们需要处理一下可能会越界的情况，可以先写出状态转移方程

从左往右：通过画图我们发现，当前位置的填写需要前一个位置和nums的前一个位置相加

此时j-1，如果从下标为0开始填写的话，j-1肯定会越界，所以要么一开始就处理j=0的时候，要么就开辟辅助空间，直接从j=1位置开始填写

同理从右往左：我们填写的时候需要借助j+1的位置和nums[j+1]的元素，所以可能会越界

这里我们都选择辅助空间，所以前面开一个，后面开一个，一共多开两个空间

注意：使用辅助空间的时候要清楚各个下标的对应关系，也就是你dp数组的下标要对应+的话是+nums数组的哪个（通过画图自己分析）（前缀和想要强化可以看我动态规划章节）

class Solution {
public:int pivotIndex(vector<int>& nums) {// 创建一个二维数组// dp[0][j]:从左往右// dp[1][j]:从右往左// 如果两个对应相等即返回，如果没有则返回-1int n = nums.size();vector<vector<int>> dp(2, vector<int>(n + 2)); // n+2边界处理dp[0][1] = dp[1][n] = 0;// dp[0][j]=dp[0][j-1]+nums[j-1];for (int j = 2; j < n + 1; j++) {dp[0][j] = dp[0][j - 1] + nums[j - 2];}for (int j = n - 1; j > 0; j--) {dp[1][j] = dp[1][j + 1] + nums[j];}for (int i = 1; i < n + 1; i++) {if (dp[0][i] == dp[1][i]) {cout << i;return i - 1;}}return -1;}
};

leetcode238例题

算法原理讲解：题目其实有提示，前缀和和后缀和

解法一：暴力解法，每个位置都需要从前往后算，时间复杂度O(N^2)；

解法二：前缀和

比如数组{1，2，3，4}，我们要算3这个位置的话

可以算前缀和1*2，后缀和4

所以相乘就是8，所以这个位置是8

所以我们可以开辟一个dp二维数组，第0行填前缀，第一行填后缀，要算某个位置就是前缀*后缀

注意：这里0的位置和n-1的位置填写是有讲究的，可以自己试一下，发现填1可以填0不行

class Solution {
public:vector<int> productExceptSelf(vector<int>& nums) {int n = nums.size();vector<vector<int>> dp(2, vector<int>(n));dp[0][0] = dp[1][n - 1] = 1;for (int j = 1; j < n; j++) {dp[0][j] = dp[0][j - 1] * nums[j - 1];}for (int j = n - 2; j >= 0; j--) {dp[1][j] = dp[1][j + 1] * nums[j + 1];}vector<int> ret;for (int i = 0; i < n; i++) {ret.push_back(dp[0][i] * dp[1][i]);}return ret;}
};

leetcode560例题

算法原理讲解

一、暴力枚举

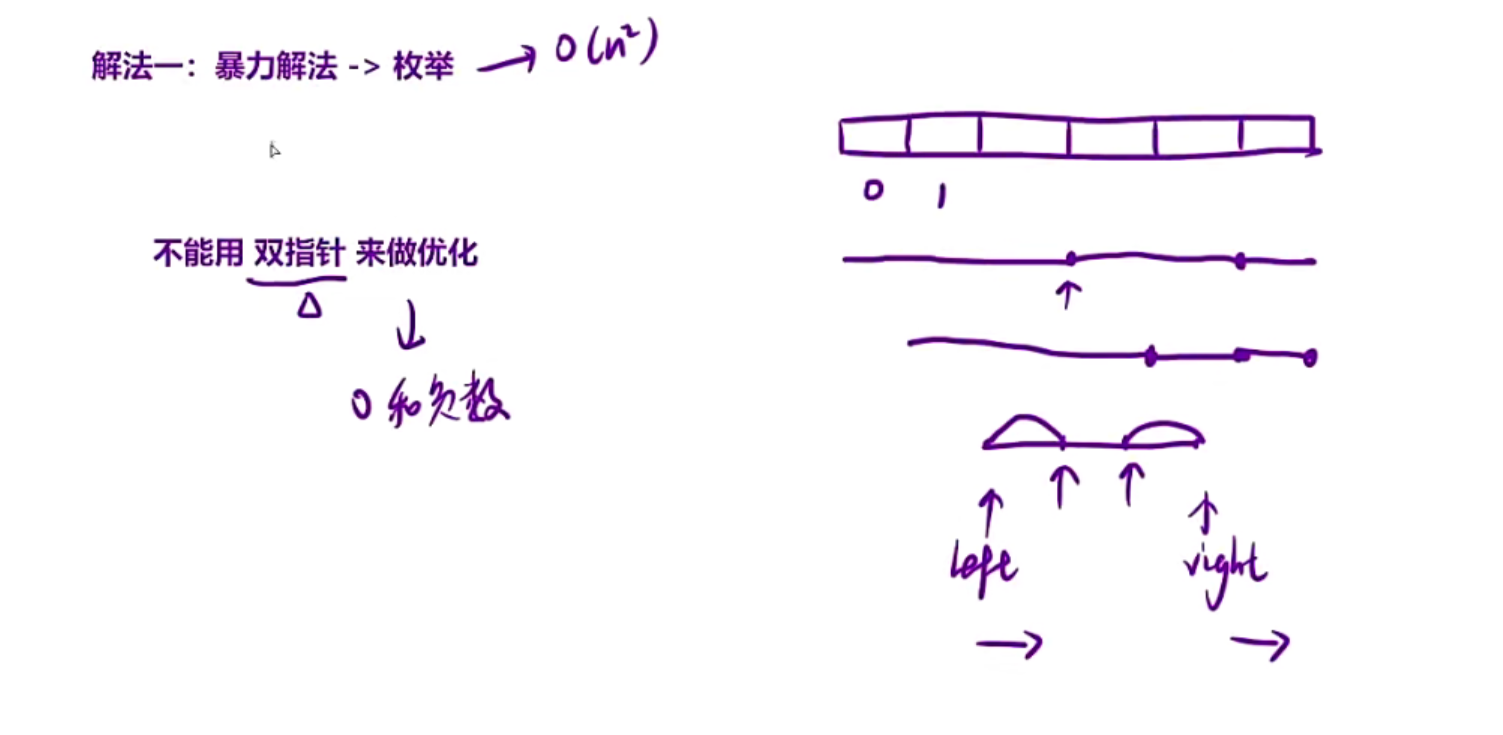
暴力枚举是你枚举每一个子数组，但是注意题目当中是有0和负数的，所以你枚举到一个和为k的时候不能停，接着往下枚举，可能下面正负正负抵消了，又有合法数组，所以每次枚举的时候我们都要从头到尾

注意这里不能使用双指针（滑动窗口），因为滑动窗口是需要维持一个性质，left和right能够一直右移动，但是这里可能在left和right的中间还有符合的数组，所以right可能会左移

二、前缀和+哈希表

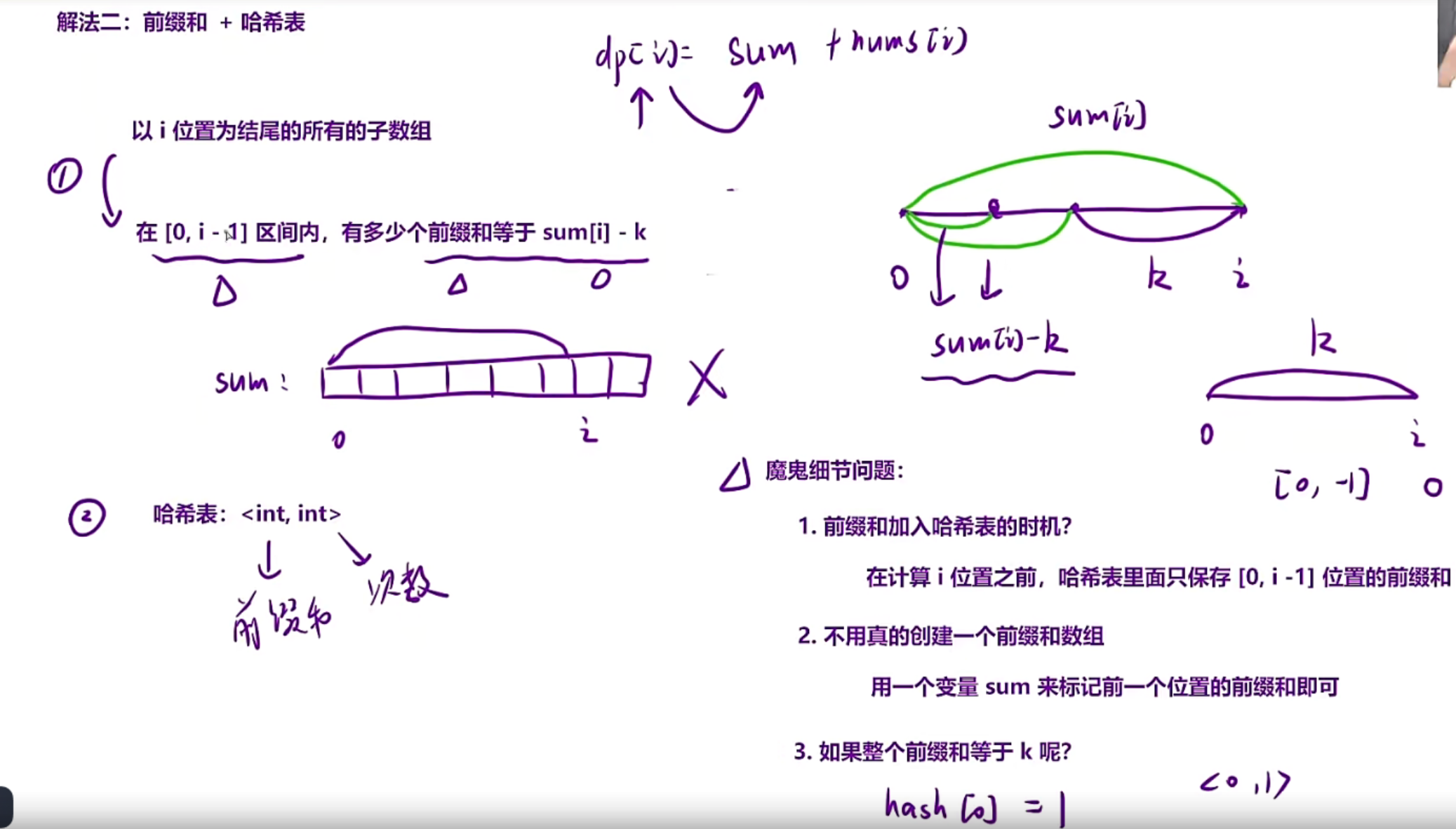
前面枚举子数组的时候，是从前往后枚举，但是这里我们选择从后往前枚举每个子数组，也就是如果你的下标为i，那你的子数组就是i，i和i-1，i和i-1和i-2，一直是i……0

以下的方法就是从i位置向前枚举子数组

dp[i]：表示以i位置为结尾的前缀和

这个整个数组的前缀和设为sum[i]，所以我们只需要在前面找到一个sum[i]-k的即可

因为这样sum[i]-(sum[i]-k)=k，（剩下的就是k了）也就是总和-部分，剩下的就是k

如果我们额外创建一个数组来存这个前缀和，首先构建前缀和就需要从前面开始遍历一遍数组

时间复杂度为O（N）

此次我们还需要统计一下算到i位置，【0，i-1】这个区间有多少个sum[i]-k，统计出来

所以每算一个位置，我们需要从前往后遍历统计，时间复杂度为O（N^2）

这样算下来还不如暴力枚举呢

所以我们可以利用哈希表来辅助，哈希表中存了前缀和和次数的对应关系

细节问题：

1.在计算i位置之前，只能保持[0,i-1]位置的前缀和，因为如果你是把所有的前缀和算出来，然后一股脑的扔到hash里面，就会导致重复计算，因为你算i位置的时候只是算i前面的子数组，并没有包括i后面的，所以如果你一股脑扔到哈希里面，就会导致后面的也算上了就会重复计算

2.可以使用一个动态滚动的方式来优化前缀和计算

比如你算i位置的时候，只需要i-1和nums[i]，那是不是不需要i-2，此时我们只需要用一个sum，不需要一个数组，sum每次更新完之后扔到哈希即可

3.如果整个前缀和，也就是下标为i的时候 0……i刚好为k，那就会去【0，-1】当中需要是否有0

所以我们初始化哈希的时候要给0一次，否则就会导致出错

这个代码示例是创建dp数组的

class Solution {
public:int subarraySum(vector<int>& nums, int k) {// 注意不能够一股脑把前缀和扔到哈希中int n = nums.size();unordered_map<int, int> hash;hash[0] = 1; // 细节处理int sum = 0;; // 用来统计dp数组的vector<int> dp(n);dp[0] = nums[0];hash[nums[0]]++;if (dp[0] == k)sum++;for (int i = 1; i < n; i++) {// 先计算前缀和dp[i] = dp[i - 1] + nums[i];// 判断有没有合法的子数组sum += hash[dp[i] - k];hash[dp[i]]++;}return sum;}
};

这个代码是滚动数组，没有创建dp数组，而是使用变量来统计

总结这道题：平时我们是从前往后枚举每个子数组，但是这里是从后往前枚举，并且有三个细节问题，尤其是hash[0]=1

leetcode974例题

知识点补充：

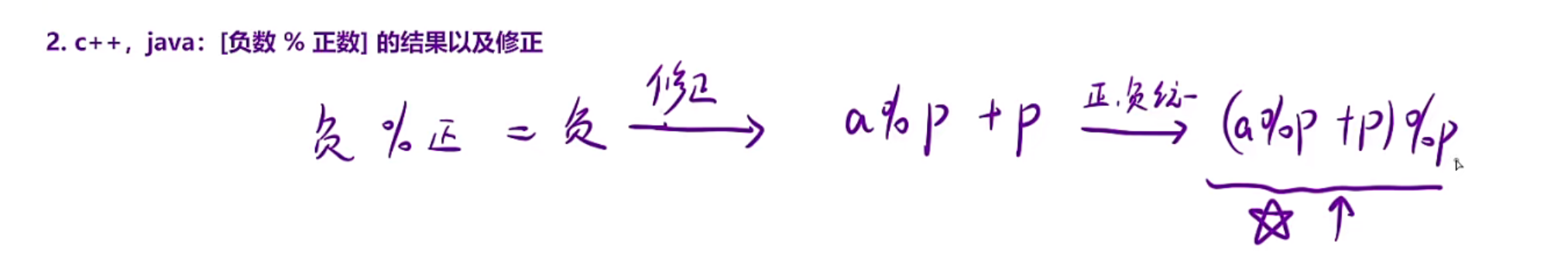
对于c++和Java，负数%正数=负数（这里和数学当中是不一样的），所以需要修正

a为负数，p为正数，需要把结果负数变正数a%p+p，但是此时正数就会错，所以需要(a%p+p)%p

正数的话(a%p+p)%p，就相当于a%p%p，负数的话就对的

算法原理和560例题是一样的

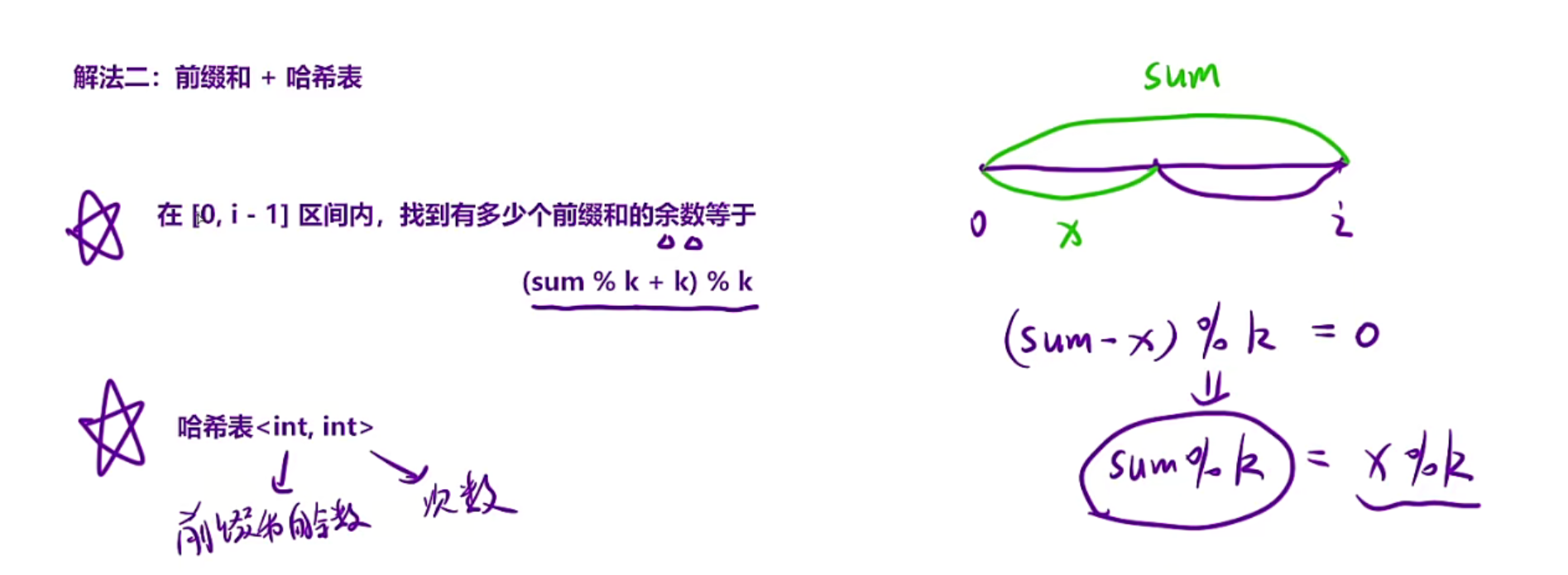
也就是在前面寻找有多少个sum%k=x%k的，但是sum可能是负数，所以要修正

然后细节问题的话和前面一样

也要把hash[0]=1，因为你后算计算的时候，可能一整个sum%k是可以被整除的，此时他就会找去前面寻找sum-sum=0；0%k有没有存在，简单来说我们是找0到i-1这段区间，但是为什么表明0-i这段区间也合法，就需要额外处理，hash[0] = 1 确保了 “整个数组” 这个子数组被统计进去。如果没有这个初始化，这类从起始位置开始的有效子数组会被遗漏。

class Solution {
public:int subarraysDivByK(vector<int>& nums, int k) {unordered_map<int,int>hash;hash[0]=1;//细节问题int sum=0,ret=0;for(auto x:nums){//计算前缀和的余数sum+=x;ret+=hash[(sum%k+k)%k];//计算余数,并且在hash当中寻找有多少个//更新hashhash[((sum%k+k)%k)]++;}return ret;}
};

leetcode525例题

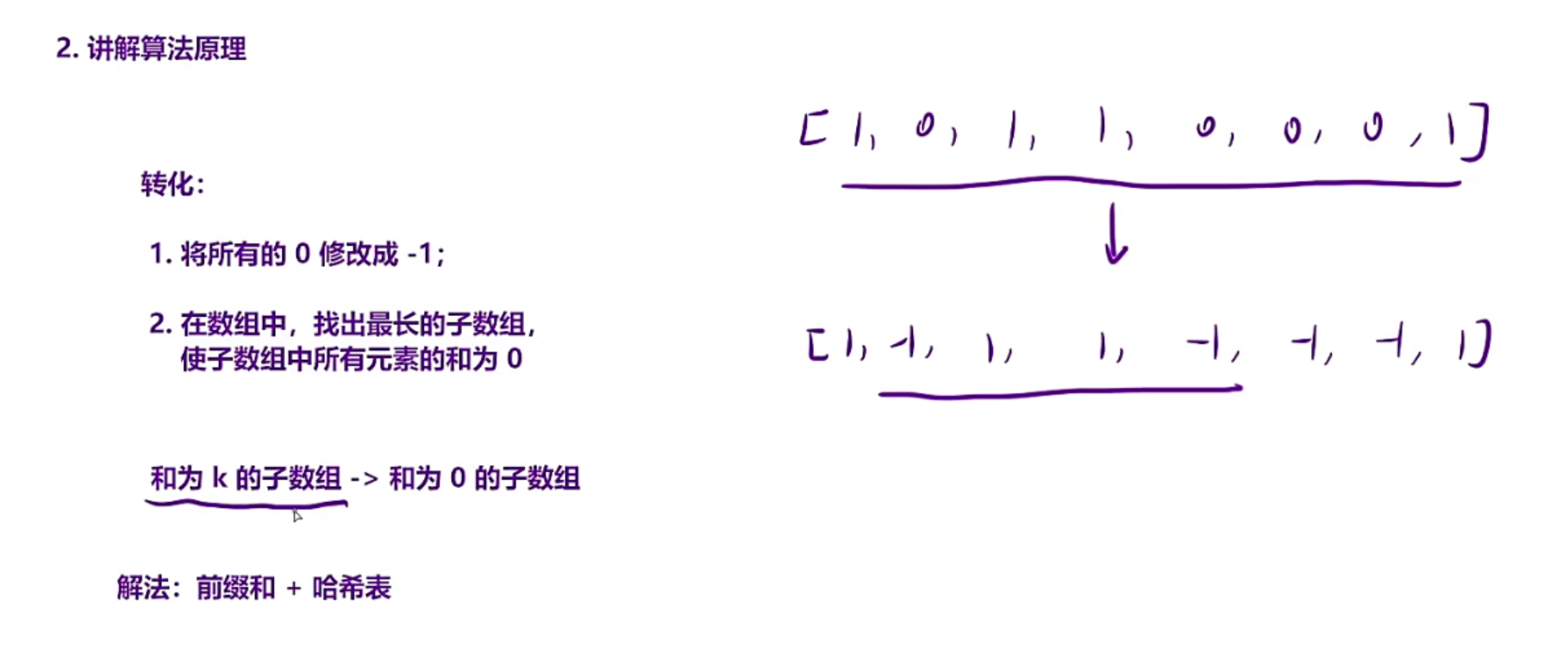
通过这一步转换，就可以把问题转换成和为0的子数组，和560例题有点类似

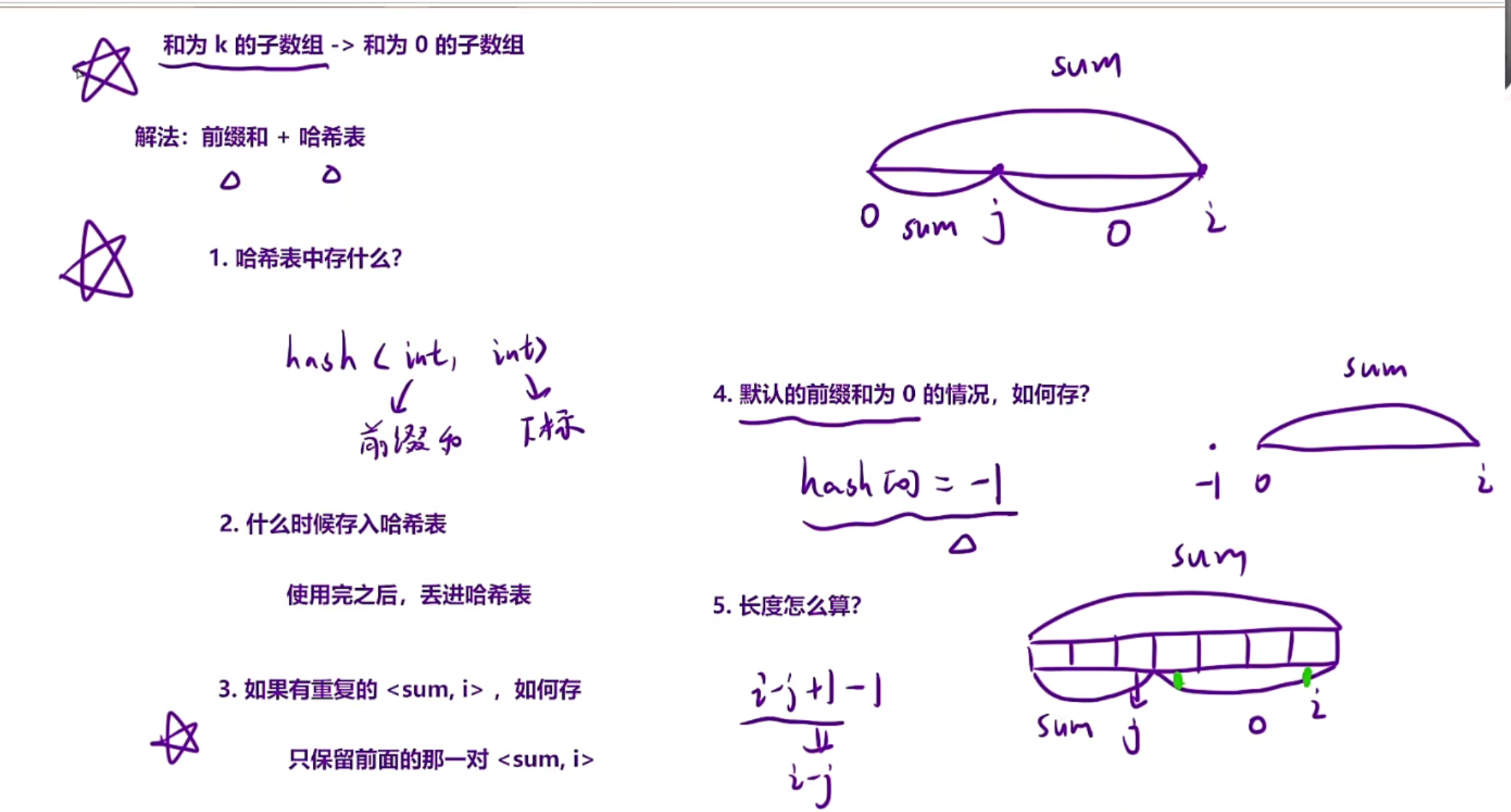
细节问题：

1.由于这道题是找符合的最长的子数组，所以hash当中应该存<前缀和，下标>

2.什么时候存入哈希表，应该是在用完i位置之后，然后更新哈希

3.如果有重复的<sum,i>，如何存，不能更新，应该保留之前的，因为我们找的是最长的，最长肯定是离i位置最远的，所以应该让最远的保留下来

4.如果sum本身就是前缀为0，那我们就需要特殊处理一下，让hash[0]=-1，只有这样在hash当中做减法的时候才会对，比如你sum有6个元素，下标应该是5，5-（-1）=6这样才能对

5.长度应该怎么算？

假设前面j位置我们找到一个sum，hash[sum]=j，那此时的长度应该是i-j

class Solution {
public:int findMaxLength(vector<int>& nums) {for (auto& e : nums) {if (e == 0) {e = -1;}}int n = nums.size();unordered_map<int, int> hash;//存的是<前缀和，下标>hash[0]=-1;//特殊处理int sum = 0,ret=0; // 滑动数组+ret记录for (int i = 0; i < n; i++) {sum += nums[i];if(hash.count(sum)){//如果存在的话，更新ret，但更新hash，因为要最远ret=max(ret,i-hash[sum]);}else{//此时是不存在,要更新hash[sum]=i;}}return ret;}
};

leetcode1314例题

题目解析：

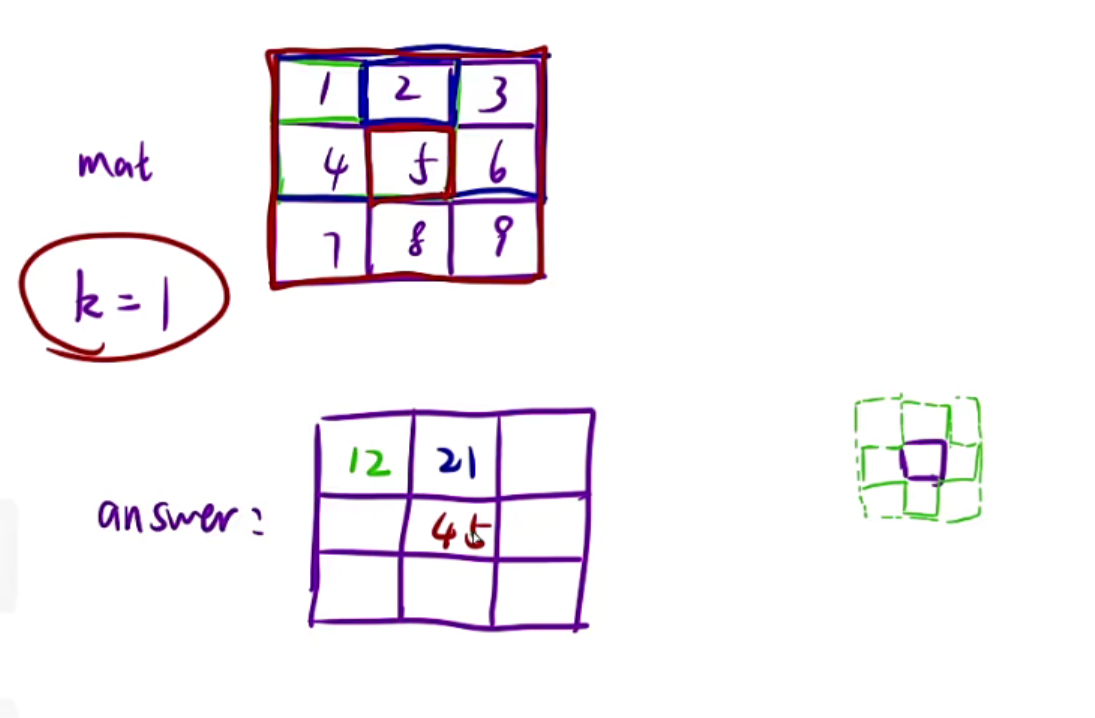
给一个矩阵mat和一个整数k，你要返回的矩阵大小和mat一样，k是告诉你算answer的时候应该怎么算

在示例1中，比如k=1，算answer中间元素的时候，就需要扩展左边右边上面下面一个方格，扩展完之后就是一个矩形，所有在矩形当中的元素的和填入中间，5这个位置扩展完之后就是整个，那就是1+2+3+4+……+9，也就是45

假如算answer[0][0]，这个位置，因为k=1，以00为中心扩展一个方格的正方形，所以就是1+2+4+5=12，因为超出边界的不算

所以k决定的是你的方格扩展多少格，如果k=2那就是5x5的矩阵和了因为你左边扩展2个，右边扩展两个，包括中间一个，那就是5x5

所以示例2，5x5的矩阵全包了，所以所有的返回都是45

算法原理讲解

前缀和：

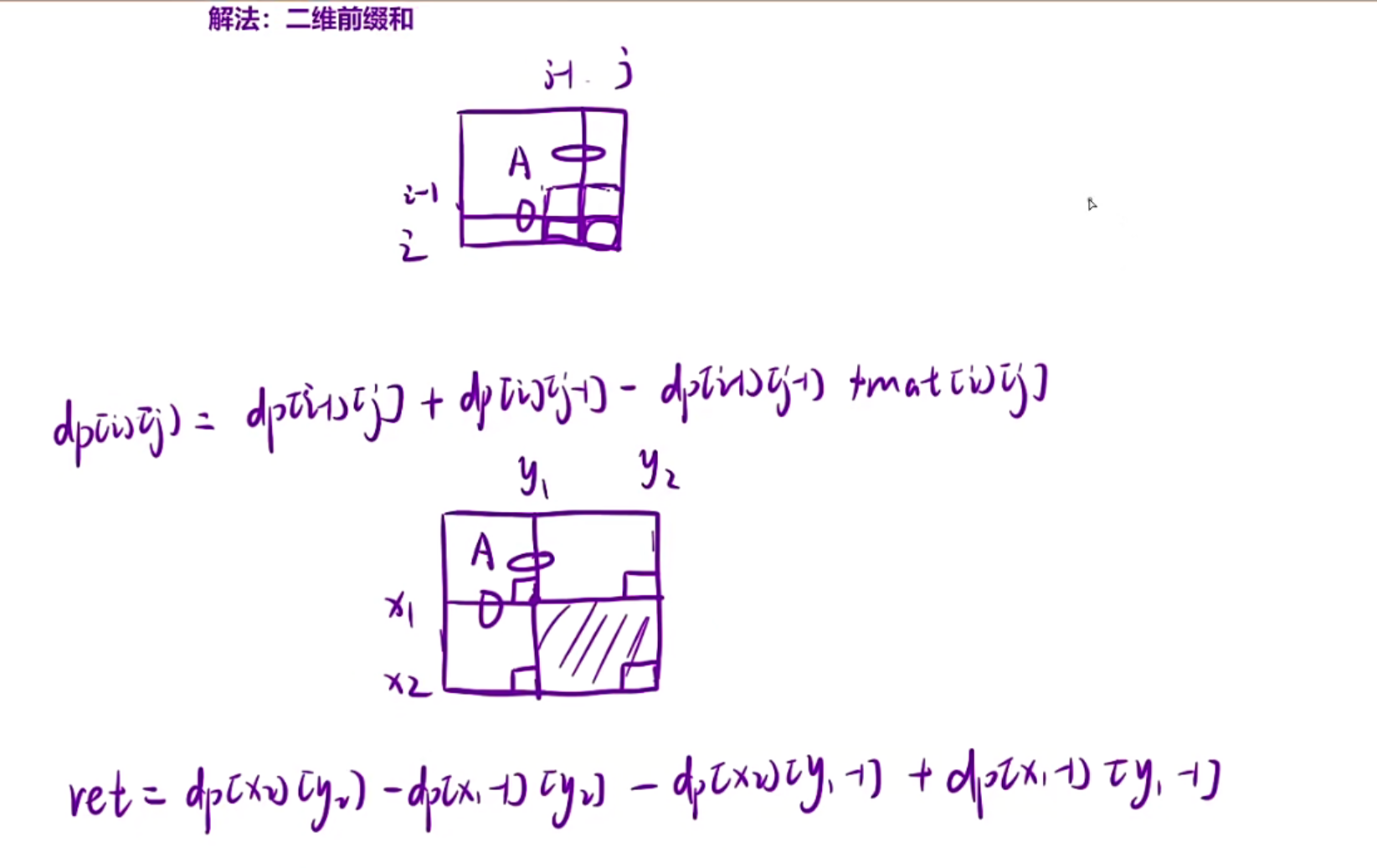
前缀和计算ret的时候需要知道左上角和右下角的坐标，所以细节一就是怎么求坐标，然后带到dp

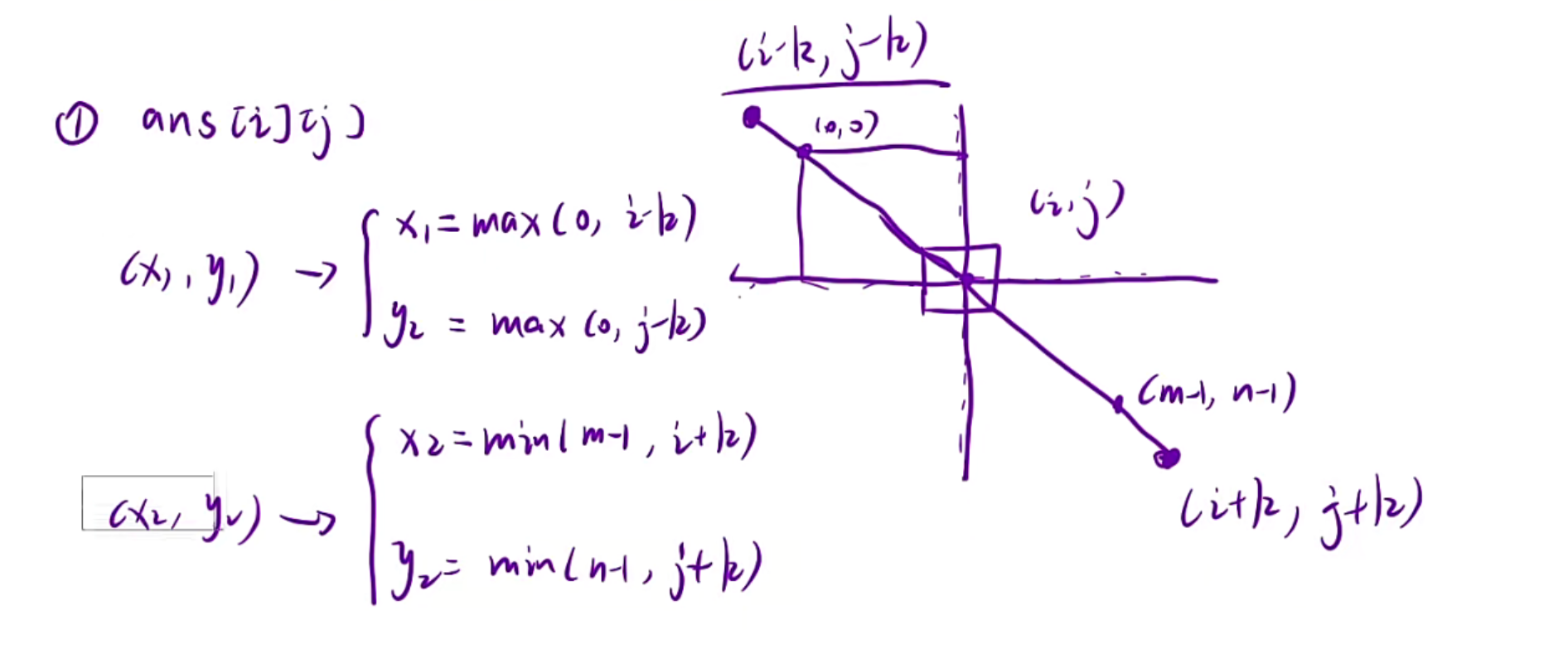
因为k代表了向四周扩展多少个格子，所以我们求左上角和右下角的坐标时就是原点+-k

但是可能会越界，如果越界了就算到边界即可

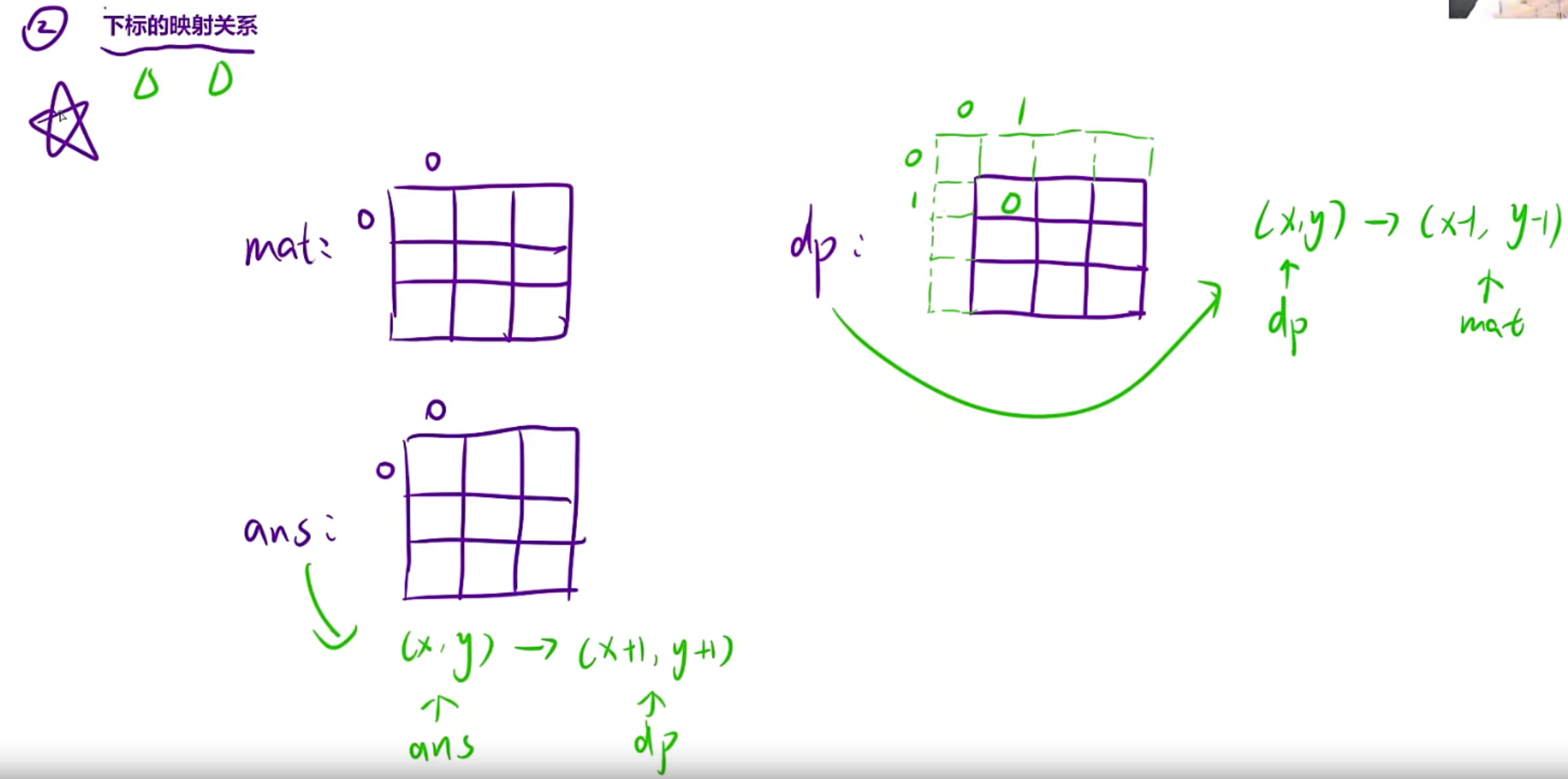
使用辅助数组，让我们更好的处理边界情况，因为上面我们在找dp的递归公式的时候，发现可能会越界，比如你填写【0，0】这个位置的时候，dp是不是会越界访问了，所以为了更好的填写dp表，我们需要额外的开辟空间来辅助填写

对于ans也要注意下标映射，在求的时候，要么最后面的公式每个坐标+1，要么直接在求x1求完之后+1，后面直接带入就行

class Solution {
public:vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {int m=mat.size();int n=mat[0].size();vector<vector<int>> dp(m+1,vector<int>(n+1));//多开一行多开一列vector<vector<int>> ans(m,vector<int>(n));//保存结果//1.填写dp表for(int i=1;i<m+1;i++){for(int j=1;j<n+1;j++){dp[i][j]=dp[i][j-1]+dp[i-1][j]-dp[i-1][j-1]+mat[i-1][j-1];}}//2.根据dp表来填写ansfor(int i=0;i<m;i++){for(int j=0;j<n;j++){ //先计算方格扩展之后的左上角坐标和右下角坐标int x1=max(0,i-k);int y1=max(0,j-k);int x2=min(m-1,i+k);int y2=min(n-1,j+k);//填写的时候注意下标的映射ans[i][j]=dp[x2+1][y2+1]-dp[x1][y2+1]-dp[x2+1][y1]+dp[x1][y1];}}return ans;}
};

总结：

前缀和是一种高效计算「区间和」的预处理技术

当题目出现以下特征时，优先考虑前缀和：

1. 核心需求是「区间和」题目明确要求计算「子数组 / 子矩阵的和」，或可转化为区间和问题（如 “子数组和为 k”“子矩阵和不超过 k”）。

   例：

   • 给定数组，求所有长度为 m 的子数组的和 → 前缀和可 O (1) 计算每个区间和。
   • 给定矩阵，多次查询任意子矩阵的和 → 二维前缀和预处理后，每次查询 O (1)。

2. 需要「多次查询」或「批量计算」如果只需计算一次区间和，直接遍历即可（O (n)）；但如果需要多次计算不同区间的和（尤其是大量查询），前缀和的预处理（O (n)）+ 单次查询（O (1)）会显著提升效率。

3. 可结合哈希表优化计数问题当题目要求「统计满足某种和条件的区间数量」时（如和为 k、和能被 k 整除），前缀和 + 哈希表（记录前缀和出现次数）是经典解法，时间复杂度可从 O (n²) 降至 O (n)。

可以理解为：前缀和是 DP 的一个特例，专门用于解决区间和相关问题，而 DP 是更通用的解题框架，可处理更复杂的状态依赖。

注意：

我们使用前缀和算法的时候，应该小心例如hash[0]的初始化，防止后面计算出错

还有下标的映射关系等等

并且学会不同题型的举一反三