数据结构（9）

目录

图的存储结构——链式存储结构

1、邻接表（链式）表示法

（1）邻接表的结构组成

（2）具体实现（分类型说明）

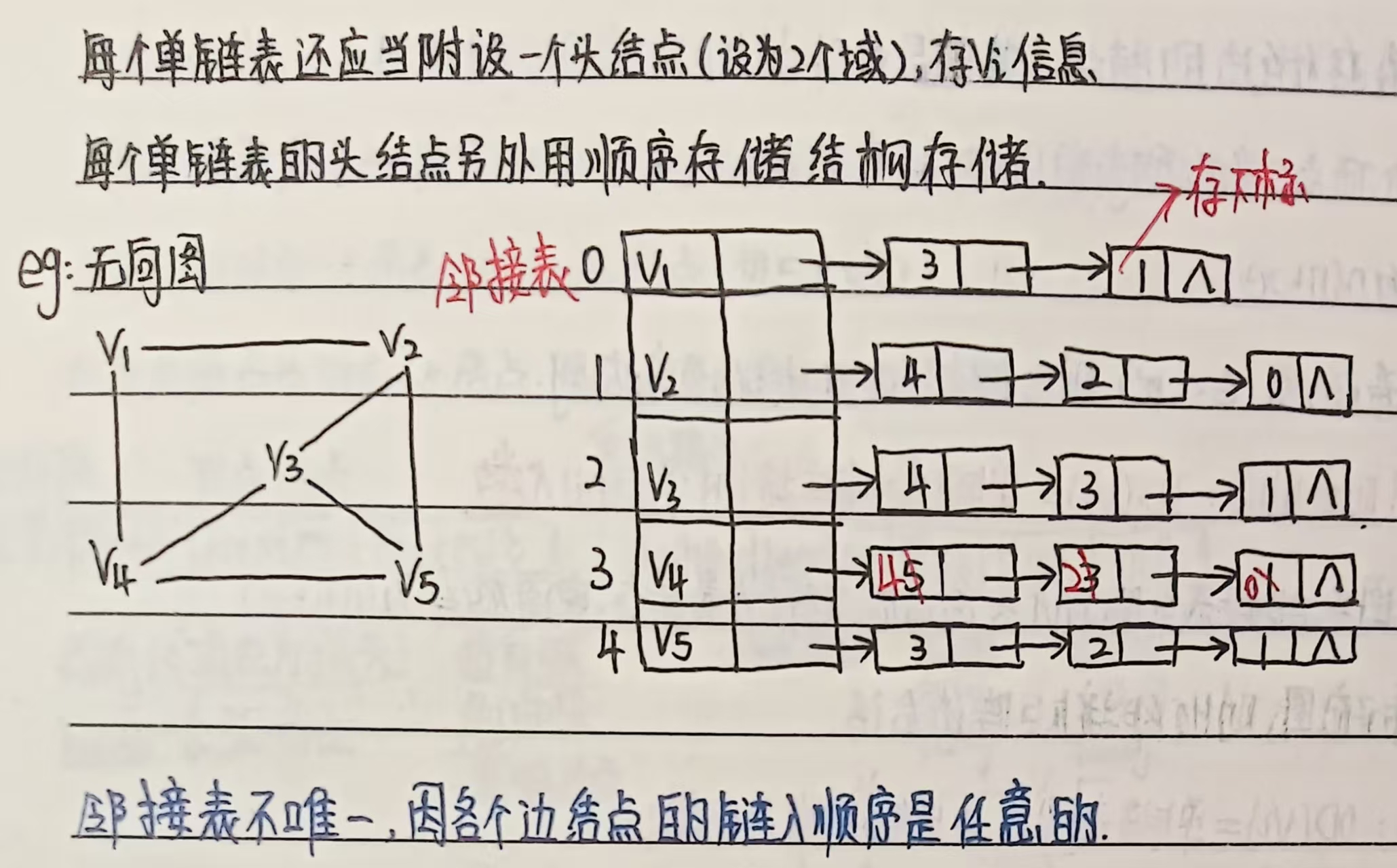
①  无向图的邻接表

②  有向图的邻接表（出边表）

③  网（有权图）的邻接表

（3）数据结构定义（Python 示例）

（4）邻接表的特点

（5）适用场景

（6）邻接表和邻接矩阵异同

（7）例题

图的存储结构——链式存储结构

1、邻接表（链式）表示法

邻接表（Adjacency List）是图的一种高效链式存储结构，通过 “数组 + 链表” 的组合形式存储图的顶点及顶点间的关系，尤其适合存储稀疏图（边数远小于顶点数的平方）。其核心思想是：为每个顶点建立一个链表，记录该顶点直接邻接的所有顶点（及边的权重，针对网）。

（1）邻接表的结构组成

邻接表由两部分组成：

1. 顶点数组（表头数组）：

   • 存储图中所有顶点的基本信息（如顶点值）。
   • 数组下标通常对应顶点的编号（便于快速访问），每个元素还包含一个指针，指向该顶点的邻接链表（记录其所有邻接顶点）。

2. 邻接链表：

   • 每个顶点对应的链表中，每个节点（称为 “边节点”）记录与当前顶点邻接的顶点信息：
     • 邻接顶点的编号（或索引）。
     • 边的权重（仅用于网，无权图可省略）。
     • 指向下一个邻接顶点的指针（形成链表）。

（2）具体实现（分类型说明）

①  无向图的邻接表

• 特点：若顶点 vi​ 与 vj​ 之间有边，则 vj​ 会出现在 vi​ 的邻接链表中，同时 vi​ 也会出现在 vj​ 的邻接链表中（即每条边对应两个边节点）。

• 示例：无向图 G=(V,E)，其中 V={0,1,2,3}，E={(0,1),(0,2),(1,2),(1,3)}，邻接表结构如下：

  顶点数组（表头）：
  [0] → 1 → 2 → null  
  [1] → 0 → 2 → 3 → null  
  [2] → 0 → 1 → null  
  [3] → 1 → null  
  

  • 表头 [0] 的链表表示：0 与 1、2 相邻；
  • 表头 [1] 的链表表示：1 与 0、2、3 相邻（因无向图边双向，0 在 1 的链表中，1 也在 0 的链表中）。

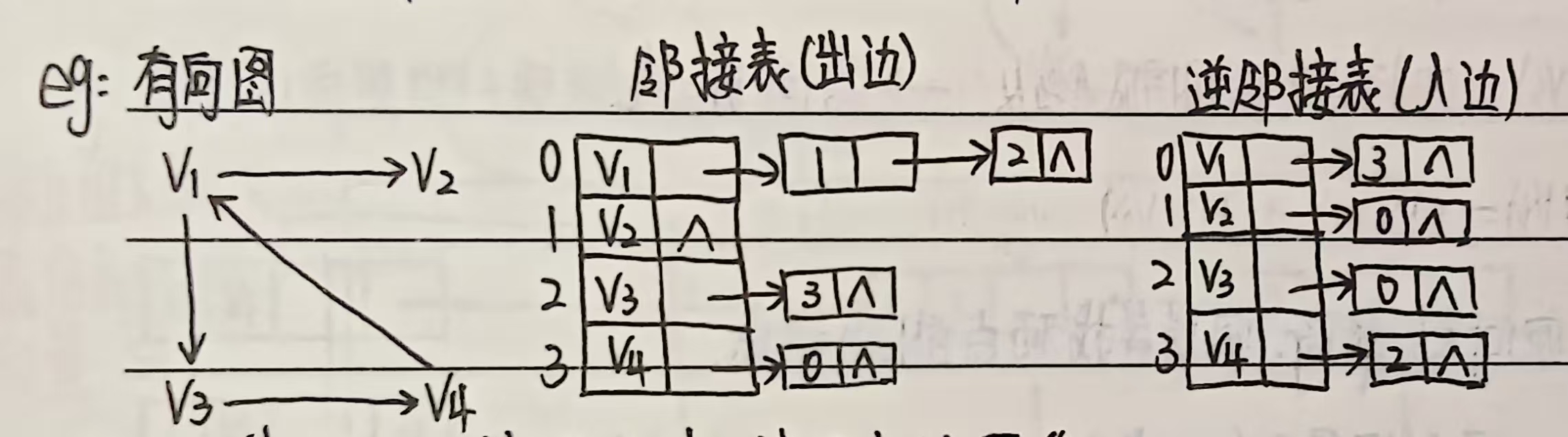
②  有向图的邻接表（出边表）

• 特点：仅记录从当前顶点出发的弧（出边），即若有弧 <vi​,vj​>，则 vj​ 仅出现在 vi​ 的邻接链表中（vi​ 不出现在 vj​ 的链表中，除非有反向弧）。

• 示例：有向图 G=(V,E)，其中 V={0,1,2}，E={<0,1>,<1,0>,<1,2>}，邻接表结构如下：

  顶点数组（表头）：
  [0] → 1 → null  
  [1] → 0 → 2 → null  
  [2] → null  
  

  • 表头 [0] 的链表表示：0 有出边到 1；
  • 表头 [1] 的链表表示：1 有出边到 0 和 2。

③  网（有权图）的邻接表

• 特点：邻接链表的每个边节点额外存储边的权重，其余结构与无权图一致。

• 示例：无向网中，边 (0,1) 权重为 5，(0,2) 权重为 3，(1,2) 权重为 1，邻接表结构如下：

  顶点数组（表头）：
  [0] → (1,5) → (2,3) → null  
  [1] → (0,5) → (2,1) → null  
  [2] → (0,3) → (1,1) → null  
  

  • 边节点 (1,5) 表示：顶点 0 与 1 相邻，权重为 5。

（3）数据结构定义（Python 示例）

class EdgeNode:"""邻接表中的边节点"""def __init__(self, adj_vex, weight=None, next=None):self.adj_vex = adj_vex  # 邻接顶点的编号self.weight = weight    # 边的权重（网用，无权图为None）self.next = next        # 指向下一个边节点的指针class VertexNode:"""顶点数组中的表头节点"""def __init__(self, data, first_edge=None):self.data = data        # 顶点的值self.first_edge = first_edge  # 指向第一个边节点的指针class AdjacencyList:"""邻接表类"""def __init__(self, vertex_count):self.vertices = [VertexNode(i) for i in range(vertex_count)]  # 顶点数组def add_edge(self, v1, v2, weight=None, is_directed=False):"""添加边（v1到v2），is_directed=False表示无向图"""# 添加v1到v2的边new_edge = EdgeNode(v2, weight, self.vertices[v1].first_edge)self.vertices[v1].first_edge = new_edge# 无向图需添加v2到v1的边if not is_directed:new_edge = EdgeNode(v1, weight, self.vertices[v2].first_edge)self.vertices[v2].first_edge = new_edge

（4）邻接表的特点

优点：

1. 空间效率高：存储 n 个顶点、e 条边的图时，空间复杂度为 O(n+e)（顶点数组 O(n) + 边节点 O(e)，无向图为 O(n+2e)），适合稀疏图（e≪n2），避免邻接矩阵的空间浪费。

2. 便于遍历邻接顶点：访问一个顶点的所有邻接顶点时，只需遍历其邻接链表，时间复杂度为 O(k)（k 为该顶点的度），效率高于邻接矩阵的 O(n)（需扫描整行）。

3. 灵活性强：适合动态增删边（只需修改链表指针），尤其适合顶点数固定但边数频繁变化的场景。

缺点：

1. 判断两顶点是否相邻效率低：若要判断顶点 vi​ 与 vj​ 是否相邻，需遍历 vi​ 的邻接链表（时间复杂度 O(k)，k 为 vi​ 的度），而邻接矩阵可直接通过 A[i][j] 以 O(1) 完成。

2. 有向图的入度查询不便：邻接表（出边表）仅记录出边，若需查询顶点的入度，需遍历所有顶点的邻接链表（时间复杂度 O(n+e)），此时可额外建立 “逆邻接表”（记录入边）解决。

（5）适用场景

• 稀疏图或稀疏网（如社交网络中的用户关系、公路网中的城市连接）。
• 需频繁遍历顶点的邻接顶点的操作（如广度优先搜索 BFS、深度优先搜索 DFS）。
• 边的增删操作频繁的场景。

（6）邻接表和邻接矩阵异同

相同点：

1. 存储目标一致：均用于存储图的顶点集合和顶点间的边（或弧）关系，能完整表示图的结构（包括无向图、有向图、无权图、网）。

2. 支持基本图操作：均可实现图的创建、边的增删、顶点遍历（如 DFS、BFS）、度的计算等基础操作，只是实现效率不同。

3. 顶点信息的存储方式：通常都需要一个数组（或类似结构）存储顶点的基本信息（如顶点值），邻接矩阵的行 / 列下标、邻接表的表头数组下标均对应顶点编号。

不同点：

对比维度	邻接矩阵	邻接表
存储结构	二维数组（n×n，n为顶点数），用数组元素值表示边的存在 / 权重。	「顶点数组 + 邻接链表」：顶点点数组存顶点信息，每个顶点对应联一个链表，记录其邻接顶点及边的权重。
空间复杂度	O(n2)，与边数无关（即使边很少，仍需占用n2空间）。	O(n+e)（e为边数）：无向图为O(n+2e)，有向图为O(n+e)，空间随边数动态变化。
适用场景	稠密图（边数e≈n2），如完全图。	稀疏图（边数e≪n2），如社交网络、公路网。
判断两顶点邻接	效率高：直接查A[i][j]，时间复杂度O(1)。	效率低：需遍历顶点i的邻接链表，时间复杂度O(k)（k为i的度）。
遍历顶点的邻接顶点	效率低：需扫描描整行（n个元素），时间复杂度O(n)。	效率高：仅遍历邻接链表（k个元素），时间复杂度O(k)（k为i的度）。
边的增删操作	效率高：直接修改A[i][j]，时间复杂度O(1)。	效率中等：需修改链表指针（插入 / 删除节点），时间复杂度O(1)（表头插入）或O(k)（指定定位置）。
度的计算	无向图：第i行（或列）的和，时间复杂度O(n)；有向图：出度为第i行的和，入度为第i列的和，均O(n)。	无向图：顶点i的链表长度，O(k)；有向图：出度为链表长度（O(k)），入度需遍历所有链表（O(n+e)，除非用逆邻接表）。
存储冗余	稀疏图中存在大量无效值（0 或∞），空间冗余严重。	仅存储实际存在的边，无冗余，空间利用率高。

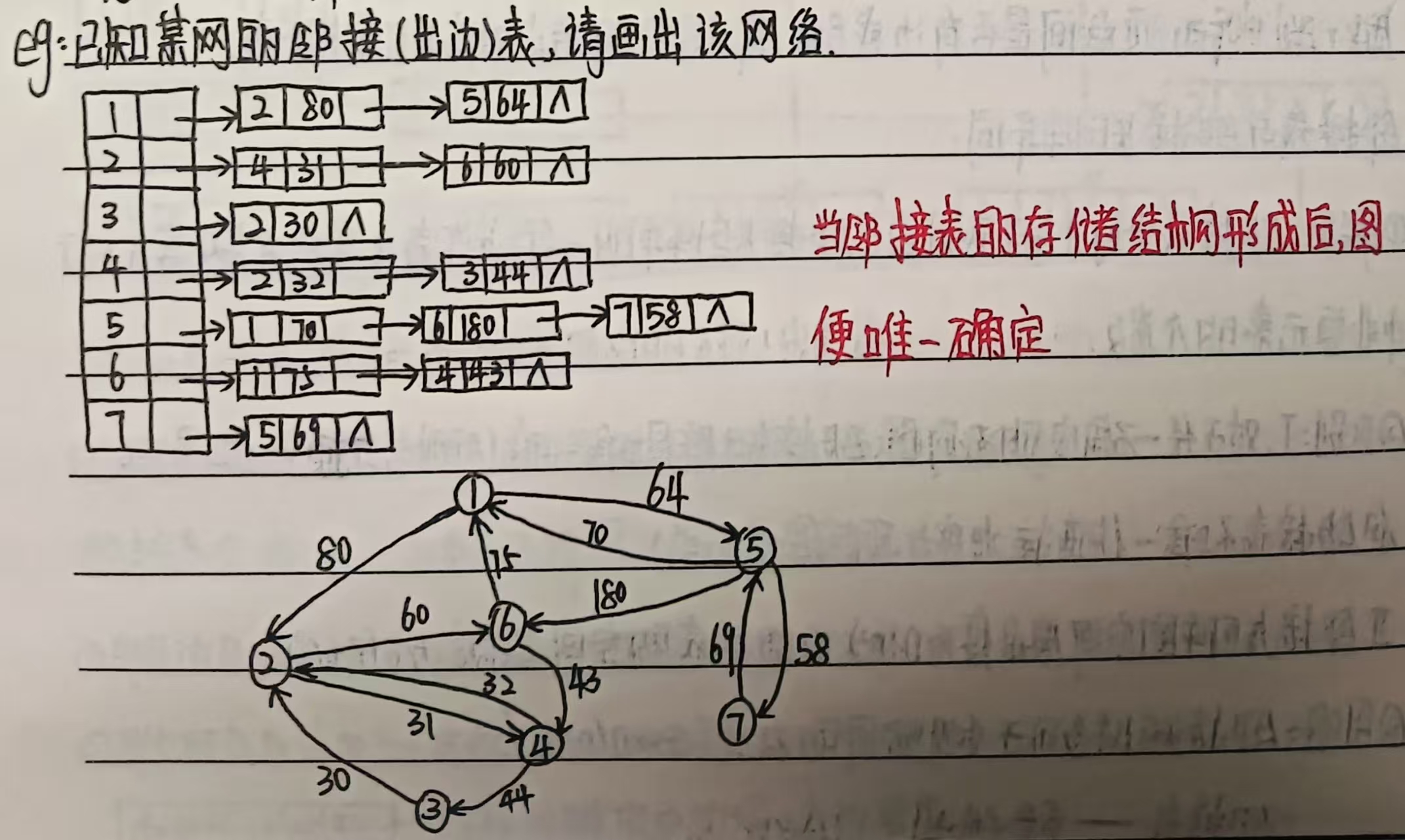
（7）例题