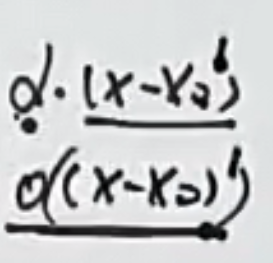一次方的高阶无穷小 = 一次方 × 无穷小
1. 基本定义回顾

2. “一次方的高阶无穷小”是什么意思?
通常,“一次方”指的是像 x 这样的一阶无穷小(当 x→0 时)。
- 那么“一次方的高阶无穷小”就是指:比 x 更快趋于 0 的量,比如 x2,x3,xsinx,x⋅o(1) 等。
- 用记号表示就是:若 ε(x)=o(x) ,那么 ε(x) 就是“一次方的高阶无穷小”。
3. 为什么说“一次方的高阶无穷小 = 一次方 × 无穷小”?
这句话的准确理解是:
任何一个比 x 高阶的无穷小,都可以写成 x⋅η(x) ,其中 η(x)→0 (即 η(x) 本身也是一个无穷小)。

4. 直观理解
- x 是“一次小”;
- 如果再乘上一个趋于 0 的东西(比如 x,sinx,x 等),整体就“更小”了;
- 所以“一次方的高阶无穷小”本质上就是“一次方再乘一个无穷小”。
例如:
- x2=x⋅x → x 是一次方,x 本身也是无穷小 → x2 是高阶无穷小;
- x⋅sinx=x⋅(无穷小) → 也是高阶无穷小;
- x⋅ln(1/x)1 (当 x→0+ )→ 虽然 ln(1/x)1→0 很慢,但仍是无穷小,所以整体仍是 o(x) 。
总结
“一次方的高阶无穷小等于一次方乘无穷小” 的意思是:
所有比 x 更高阶的无穷小量,都可以表示为 x⋅ε(x) ,其中 ε(x)→0 。
这是一种等价刻画,便于在极限计算、泰勒展开、误差分析中使用。