学习笔记｜受限波尔兹曼机（RBM）

学习来源：
6分钟快速理解受限玻尔兹曼机（RBM)
2024诺贝尔"物理学"奖成果-受限玻尔兹曼机(RBM)讲解

1. 波尔兹曼机（Boltzmann Machine，BM）

（1）BM 是一种无方向的无监督生成网络。
（2）BM = 可见节点 + 隐藏节点，没有输出节点，必须将数据输入到隐藏节点。

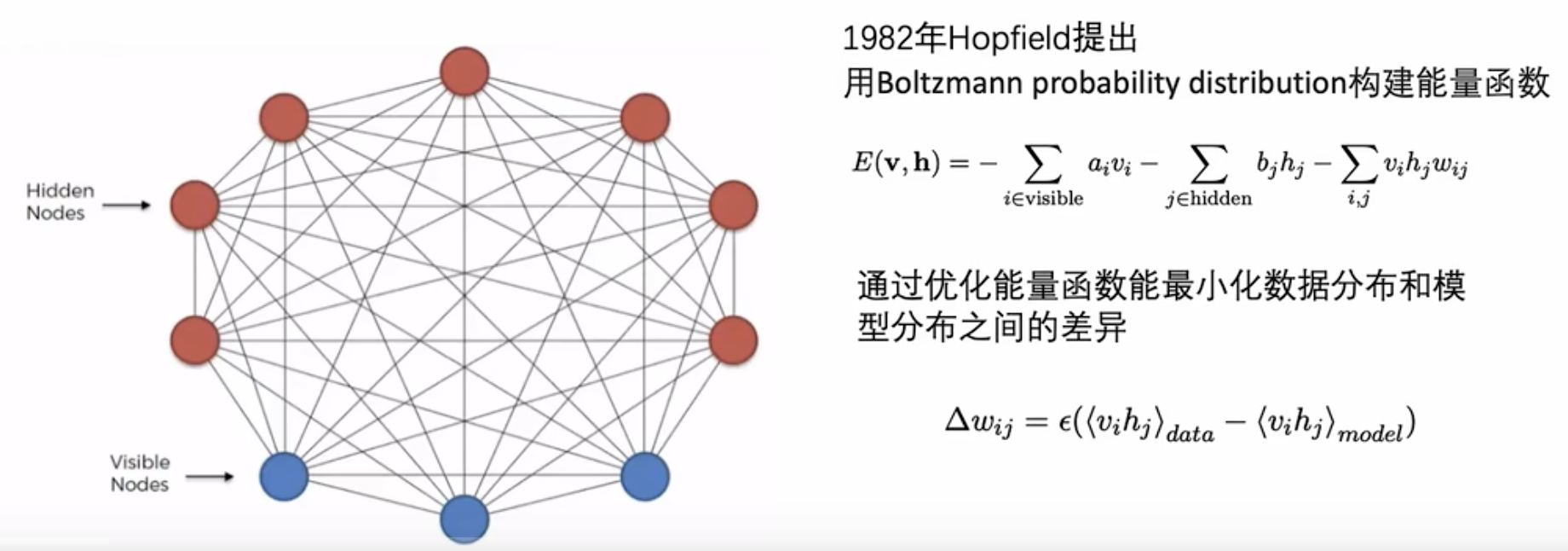
（3）缺点：不容易训练，存在过拟合风险。

2. 受限波尔兹曼机（Restricted BM，RBM）

2.1 基本概念

（1）RBM 是一种概率图模型，用于无监督学习，以发现数据中的隐藏结构。
（2）RBM 是一种2层神经网络，RBM = 1层可见单元 + 1层隐藏单元。单元间通过对称加权连接。可见单元输入数据，隐藏单元学习数据特征。

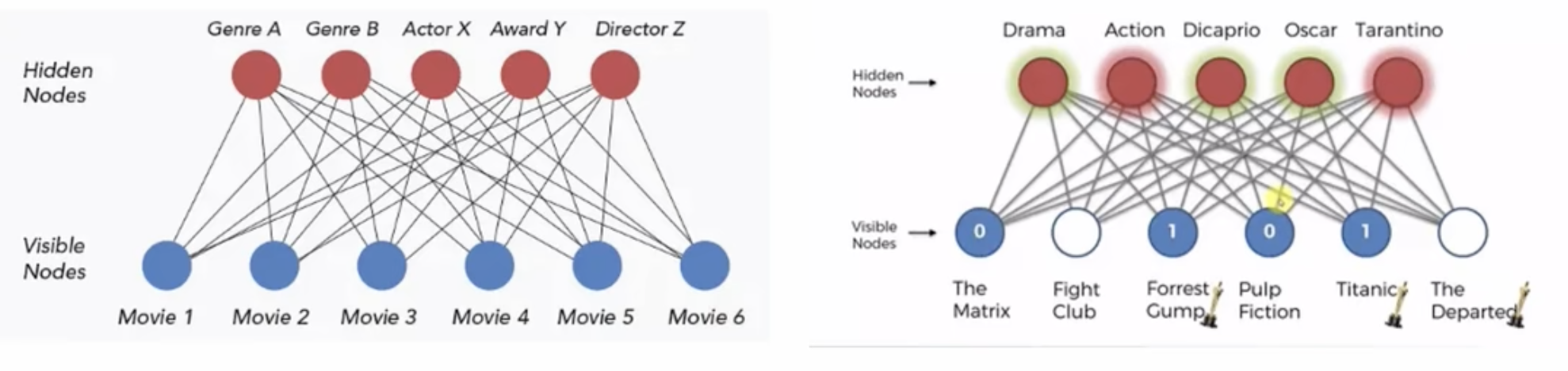
（3）不同于BM，RBM可见节点间无连接。

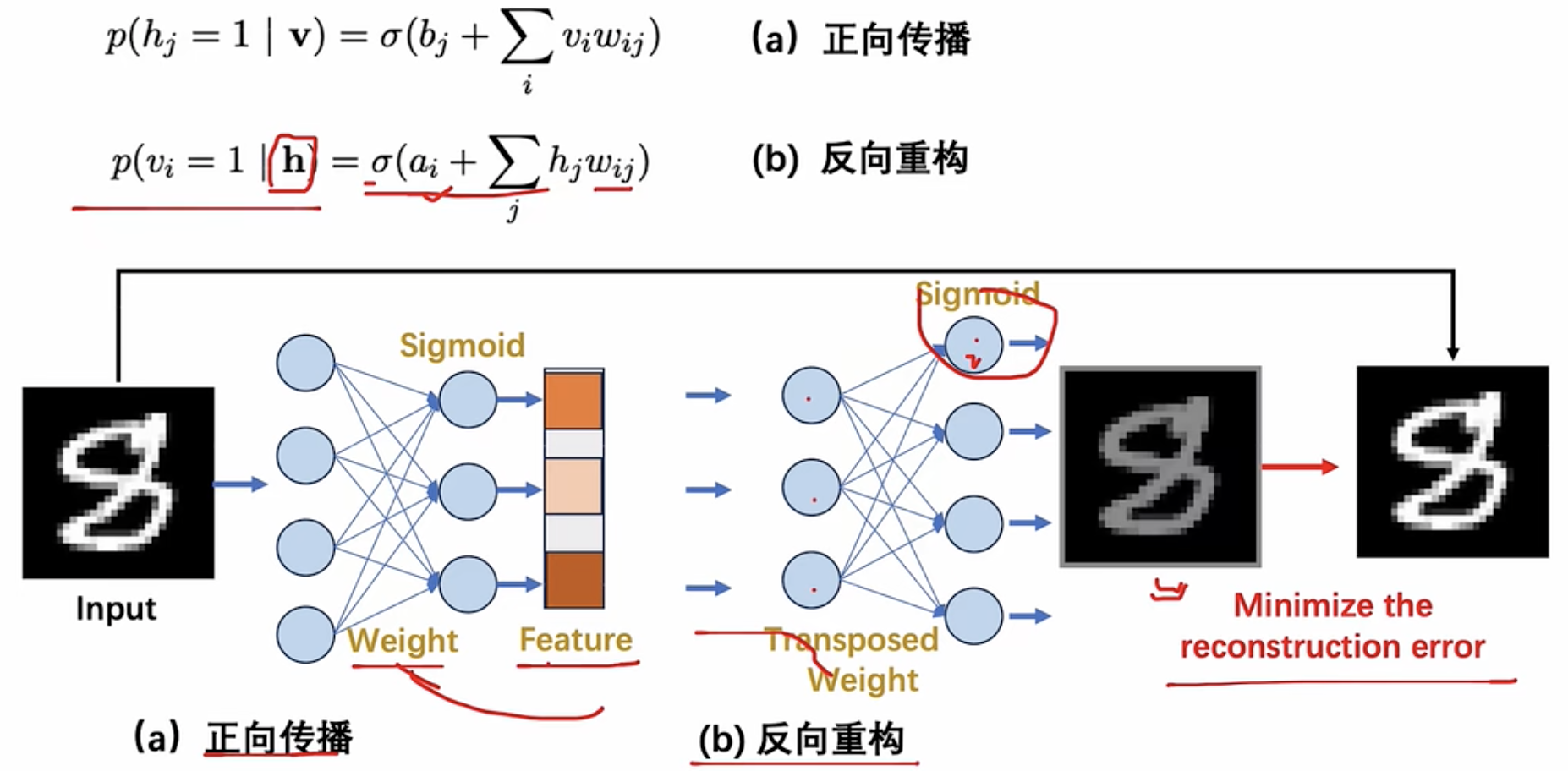
2.2 RBM的推理和应用

给定一个图像，用RBM提取特征

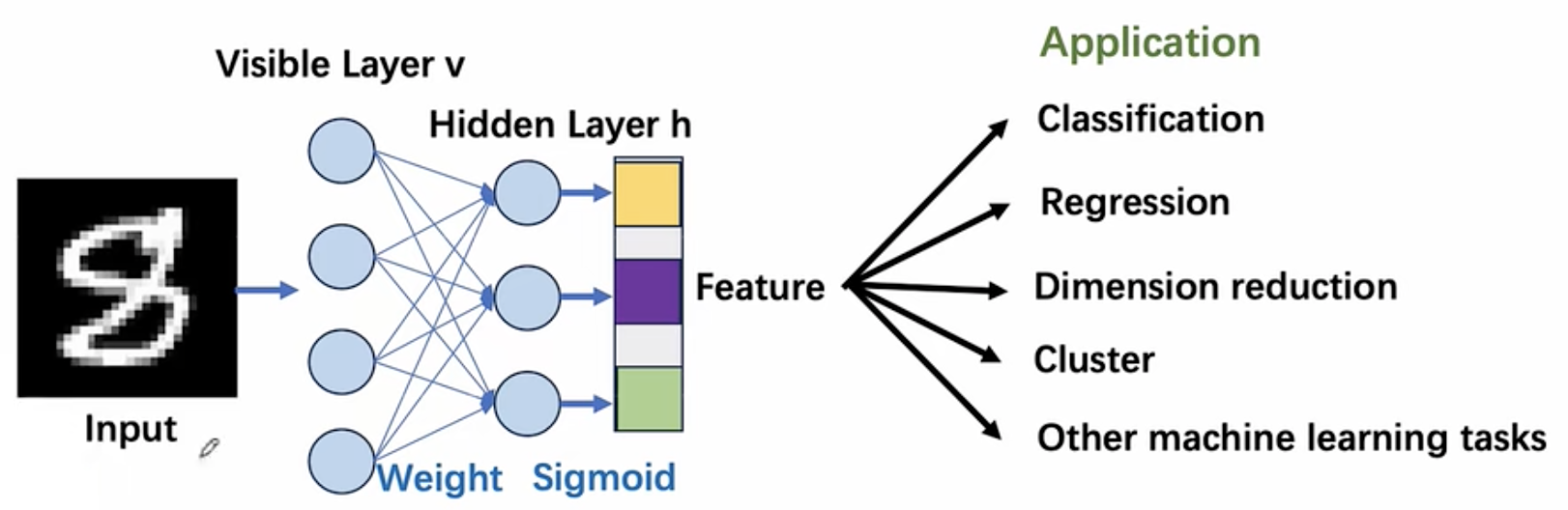
2.3 RBM的训练：Contrastive Divergence

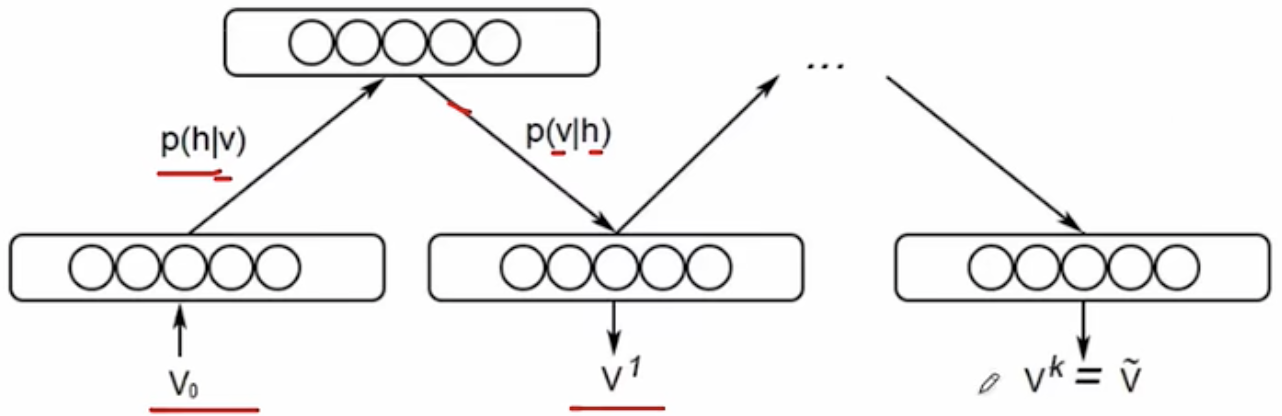
2.4 使用对比散度算法训练RBM的基本步骤

2.5 代码例子

import torch## 定义RBM
class RBM():def __init__(self,nv,nh):self.W = torch.randn(nh,nv)self.a = torch.randn(1,nh)self.b = torch.randn(1,nv)# 前馈重构过程def sample_h(self, x):wx = torch.mm(x, self.W.t())activation = wx + self.a.expand_as(wx)p_h_given_v = torch.sigmoid(activation)return p_h_given_v, torch.bernoulli(p_h_given_v) #进行伯努利采样# 反向重构过程def sample_v(self, y):wy = torch.mm(y, self.W)activation = wy + self.b.expand_as(wy)p_v_given_h = torch.sigmoid(activation)return p_v_given_h, torch.bernoulli(p_v_given_h)def train(self, v0, vk, ph0, phk):self.W += (torch.mm(v0.t(), ph0) - torch.mm(vk.t(), phk)).t() #第0轮与第k轮进行相减来做权重更新self.b += torch.sum((v0 - vk), 0)self.a += torch.sum((ph0 - phk), 0)## 训练RBM
rbm = RBM(visible_unit_num, hidden_unit_num)
for epoch in range(1, nb_epoch + 1):train_loss = 0s = 0.for id_user in range(0, nb_users - batch_size, batch_size):# 初始化 vk, v0vk = training_set[id_user:id_user+batch_size]v0 = training_set[id_user:id_user+batch_size]ph0,_ = rbm.sample_h(v0)for k in range(10):# 采样重构_,hk = rbm.sample_h(vk) _,vk = rbm.sample_v(hk)phk,_ = rbm.sample_h(vk)rbm.train(v0,vk,ph0,phk)train_loss += torch.mean(torch.abs(v0[v0>=0] - vk[v0>=0]))s += 1print('epoch:' + str(epoch) + 'loss:' + str(train_loss/s))

2.6 Mnist数据集上的实验效果

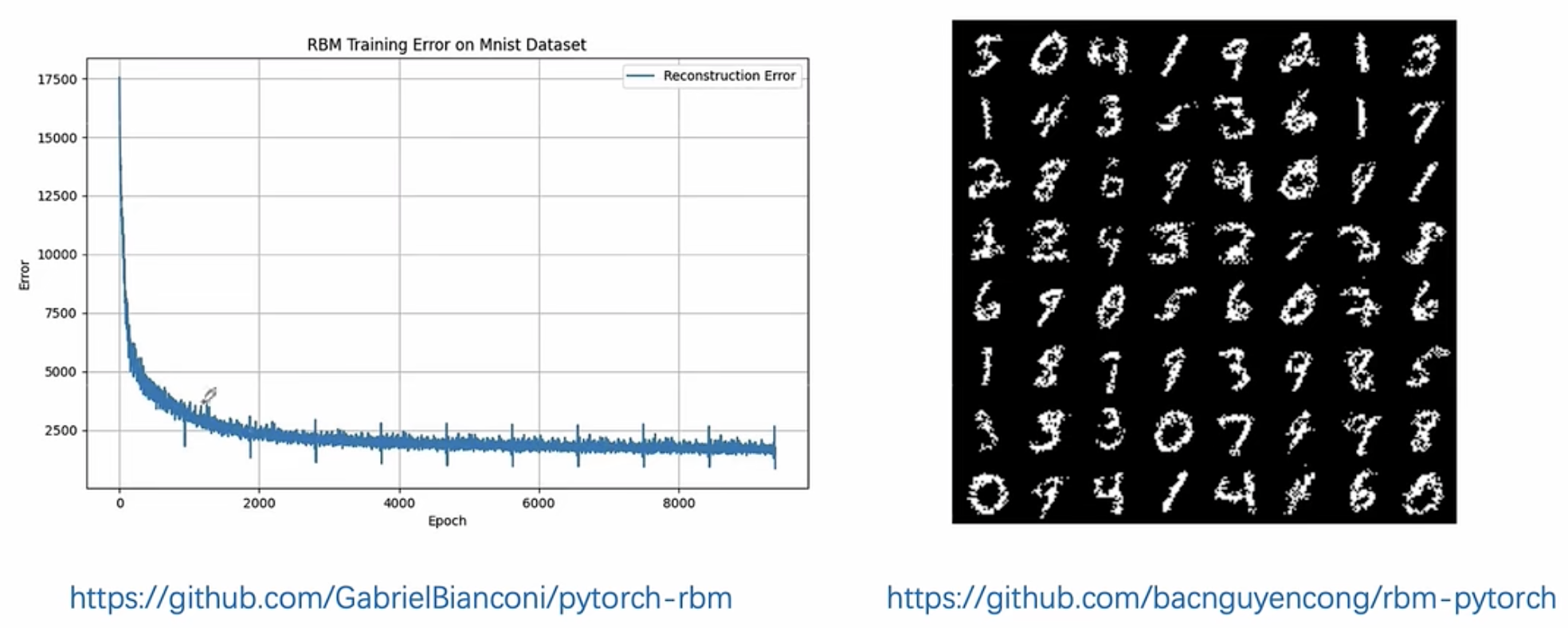
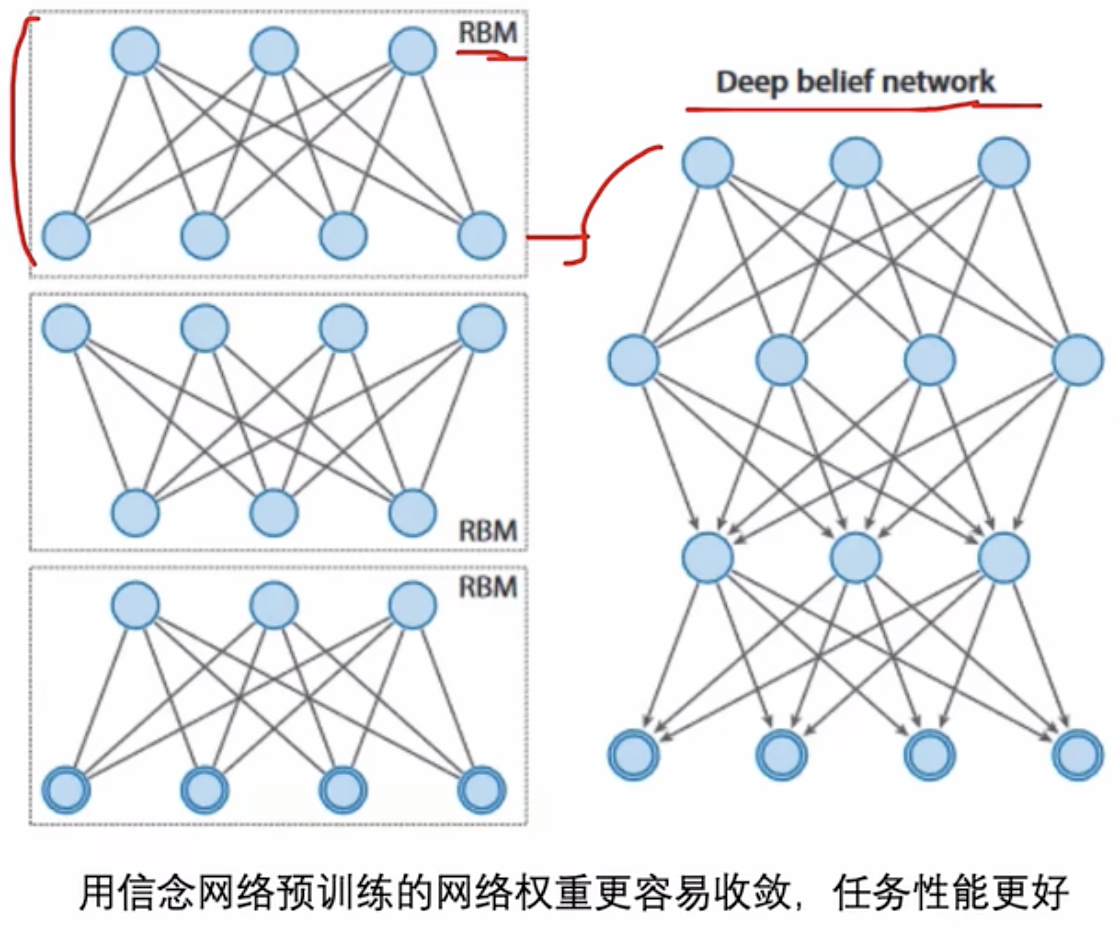
3. 发展：深度信念网络

解决早期深度学习挑战：深度神经网络不容易训练、计算机性能差