当前位置：首页 > news >正文

网络渗流：爆炸渗流

news 2025/10/26 9:00:31

一、网络渗流（percolation on networks）

网络上的渗流 - 《中国大百科全书》第三版网络版

渗流是统计物理研究的重要方向之一。物理学家最初用规则网状结构上的渗流来解释小的分子是如何通过化学键形成大分子物质的问题。在2000年左右，统计物理学家开始研究具有复杂结构的网络上的渗流，并以此为基础研究互联网上病毒传播、信息传播、网络上的破坏传播、社会行为传播、疾病传播等，成功描述了复杂网络上不同的微观传播机制与宏观的传播现象之间的丰富相变关系。
在渗流理论中，关于巨连通子网的规模与其余小子网的规模分布，主要有如下两个主要结论:

①当以巨连通子网的规模为序参量来度量其连通性时，随着删除边或者点的比例增加，其巨连通子网的规模会出现二级(连续)相变。对于多层网络，其巨连通子网规模会出现一级(不连续)的相变。

②通常，除巨连通子图之外的其余小子网的规模分布会呈现幂律分布。在远离相变点时，呈现为指数分布;在相变点上时，呈现为幂律分布。

复杂网络上渗流的种类包括:

① 边渗流。研究在按一定规则添加边或者删除边的过程中，网络中巨连通子网规模与其余子网规模分布的理论，其相变类型一定是二级相变。

② 点渗流。研究在按一定规则加点或者去点的过程中，网络中巨连通子网规模与其余子网规模分布的理论，其相变类型一定是二级相变。

③ 自助渗流。在一个顶点周围有k(参数)个顶点激活时，该顶点才会被激活的条件下，研究在按一定规则删除点的过程中，网络中最大能被激活顶点形成的巨连通子网规模的理论，一般是混合相变。

④ k-核渗流。研究按一定规则删除边或者点过程中k-核规模变化的理论。

⑤ 多层网络上的渗流。在多个网络顶点具有相互依赖的情况下，按照一定规则删除边或者点后，研究互连通网络规模的理论。当相互依赖的顶点比例比较大时，相变类型为一级相变。当相互依赖顶点比例比较小时，与单层网络一样相变类型为二级相变。

⑥ 爆炸渗流。在向网络添加边时，优先连接最小两个子网中间的顶点，形成大的连通子网，在这个过程中，研究最大连通子网规模变化的理论。在这种渗流中，最大连通子网规模会在临界点快速增长，并且是连续地增长。

二、爆炸渗流

引自：陈小龙,杨春,李志鹏,等. 复杂网络爆炸渗流研究综述[J]. 电子科技大学学报,2015,44(1): 12-21.

2007年，文献[10]引进了一个很广泛的随机网络模型族。文中对模型族中的每个模型M，存在描述
网络中最大分支的连续函数 $\rho ^{M}(t)$ ，以及存在一个临界点 $t_{c}$ ，使得当 $t<t_{c}$ 时， $\rho ^{M}(t)=0$ 。而在 $t\geqslant t_{c}$ 时， $\rho ^{M}(t)>0$ ，对于BJR模型族中所有模型来说， $\rho ^{M}(t)$ 是一个连续函数，但是在靠近临界点 $t_{c}$ 时，可能存在差异很大的临界行为。

$\rho ^{M}(t)$ 的连续性似乎是网络渗流的唯一性质，它不随模型的变化而改变。但是，2009年，文献Explosive percolation in random networks（Science,2009, 323(5920): 1453-1555.）对ER渗流模型随机连边规则进行了简单的动力学修改，引进了抑制最大连通分支生长的乘积规则(PR规则)，导致网络序参量在相变点附近产生急剧变化，并称这种现象为“爆炸渗流”(explosive percolation，EP)，且进一步指出这种渗流相变属于不连续的一阶相变。

1 Achlioptas过程下典型爆炸渗流模型：

Achlioptas过程是一个竞争过程，在该过程下可以构造许多竞争规则。这些规则又可分为有界尺
度规则与无界尺度规则两大类。

有界尺度规则指连边选择仅仅依赖于两条候选边 e1e2端点所处分支尺度。例如文献Avoiding a giant component（Avoiding a giant component）中提出的BF规则。人们推测所有有界尺度规则的渗流相变为连续的。

对于无界尺度规则，则很难利用数学理论去解释，典型的无界尺度规则有PR乘积规则和SR和规则，并且在两个规则下都可以得到“爆炸渗流”现象。

在PR乘积规则中，系统开始于N个孤立顶点，每一步都随机选取 e1e2两条候选边，将每条候选边
相关联的两个分支的尺度（大小）作乘积，取乘积最小者对应的边加入到系统中，另一条边则被丢弃，如图1所示，prob1=(7) × (2) = 14，prob2 = (4) × (4) =16 ，因此e1被选择，e2被舍弃。

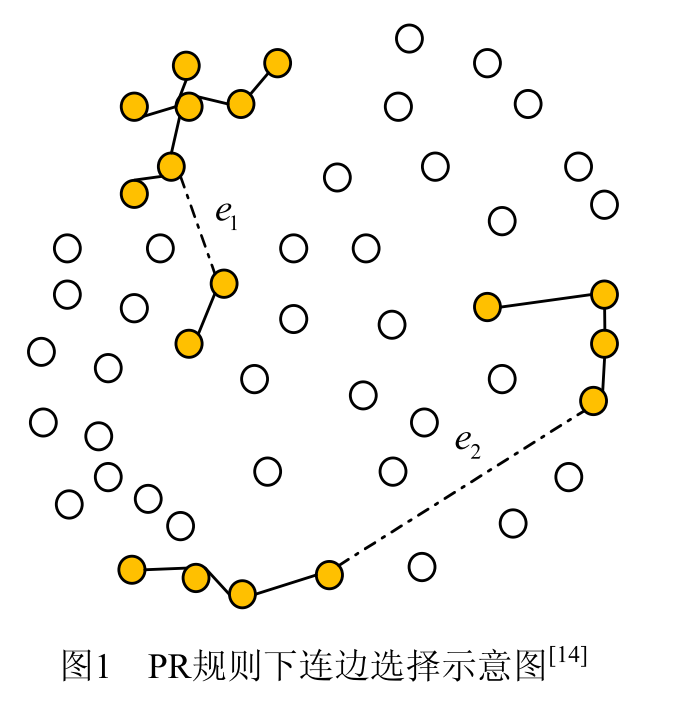
而SR和规则中，将候选边e1e2分别关联的两个分支的尺度作和，取和值最小者对应的边加入到系统中，另一条边则被丢弃。

为了研究无界尺度规则下的渗流相变情况，提出了“临界窗”的概念，定义 $t_{0}(N)$ 为最大连通分支包含节点数目小于 $N ^{\gamma }$ 时系统中添加的连边数所能达到的最大值， $t_{1}(N)$ 为最大连通分支包含节点数目大于 $AN$ 时添加到系统中的连边数所能达到的最小值，其中 $\gamma$ ， A 为两个参量。为两个状态之间加入的连边数量，称为“临界窗”长度。

局部分支聚集模型

在爆炸渗流模型构建中，一些学者将连边的选取限制到具有共同顶点的边，这样候选边涉及3个及
以上的分支，这类模型叫作局部分支聚集模型。文献Local cluster aggregation models of explosive percolation（Phys RevLett, 2010, 104(19): 195702）提出了两种局部分支聚集模型，即：邻接边模型(AE)和三角形规则模型(TR)。AE是最简单的局部分支聚集模型，该规则仍然属于抑制大分支生长的模型，但其对大分支的抑制作用较SR和规则与PR乘积规则更弱。

局部分支聚集模型的优点在于可以用数学方程描述进化过程，也就是可以建立进化过程中的微分方程，并通过Euler方法对微分方程数值求解来粗略地获得相变点位置，这样的局部过程似乎可以为分析不连续渗流提供帮助。

无标度网络渗流模型

在大量关于随机网络爆炸渗流研究展开的同时，无标度网络上的爆炸渗流也得到了广泛的关
注。他们发现在无标度网络中，AP过程对巨型分支形成的抑制作用和中心节点对巨型分支形成的促进作用相互竞争导致不连续相变不总是会发生。实验结果表明，渗流相变类型与控制参数度分布指数 $\lambda$ 密切相关。

最大分支控制模型与高斯模型

前面提到的模型共同特点是在m条候选边中通过竞争选择其中一条添加边。2010年，文献[21]提出
了只需控制最大分支生长就可以获取一阶渗流变换的最大分支控制模型与高斯调制模型。该方案在数值模拟上的一个显著优点在于可以处理比之前大64倍的系统。

最大分支控制模型在系统中随机选取一条边，如果接受它不会引起最大分支的生长或新的最大分支的形成，那么该边被添加到系统中；否则，该边被接受的概率 q1为：

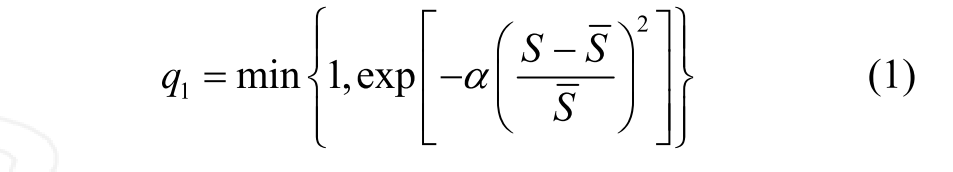
高斯模型从系统中随机选出一条边，按照概率q2：

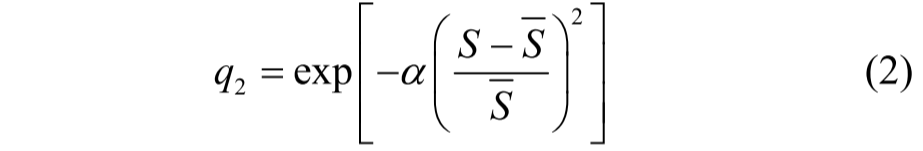
接受该边。

BFW模型

BFW模型是网络渗流研究中非常典型的模型之一，它由文献[22]在2004年提出。通过引入阶段数k
和衰减函数来判定每次从完全图中随机选择的边是否接受。

BFW模型的巨大连通分支性质对研究网络模块结构的形成过程，网络结构探测等方面均有重要
的作用。此外，多重巨大连通分支的发现在疾病传播学、高分子聚合、通信网络等方面也有一定的应用前景。

2 爆炸渗流类型

1. 不连续相变观点

早期研究（如Achlioptas等人的PR规则）认为爆炸渗流是一阶不连续相变。主要依据是数值模拟中观察到的序参量在临界点附近急剧跳跃。支持者认为，由于最大连通分支在临界点附近快速增长，表现出“爆炸性”，应归类为不连续相变。

2. 连续相变但具有异常有限尺度行为

后续研究（如Da Costa等）通过建立分支尺度分布的微分方程，发现：

在临界点处，分支尺度分布 P(S,t)满足幂律行为：P(S,t)∝S1−τ。
这表明相变本质上是连续的（二阶相变），但在有限尺度下表现出“看似不连续”的行为。

不同规则（如PR、AE、CDGM）下的爆炸渗流属于不同的普适类，具有非解析的标度函数。

3. 混合相变观点

部分研究认为爆炸渗流是混合相变，兼具连续与不连续特征：

序参量可能表现出多级跳跃或无限层次的不连续行为（如推广三角形规则）。
存在“强不连续”与“弱不连续”的区分：
- 强不连续：单条边引起的最大分支变化 ΔCmax/N 在热力学极限下为非零常数。
- 弱不连续：该比值趋于零。

3 爆炸渗流应用

1. 生物网络：蛋白质同源性网络

研究：Rozenfeld 等人 (2010)
发现：人类蛋白质同源性网络的进化过程表现出爆炸渗流特征。
机制：蛋白质通过“分支复制”事件缓慢进化，但在最后阶段，仅添加少量边就导致多个分支迅速合并成一个巨型分支。
意义：这表明生物网络的进化可能以突跃方式完成，类似于一阶相变。

2. 社会网络：论文合著与移动通信网络

研究：Pan 等人 (2011)
网络类型：移动电话网络、大型和小型论文合著网络。
规则：使用修改的最小化和规则，即每步从多条候选边中选择连接分支总规模最小的边。
发现：
- 在真实社会网络中应用Achlioptas过程确实能引发爆炸渗流。
- 网络本身的拓扑结构（如社区结构）对渗流过程有重要影响。
- 在临界点，由MC规则选中的边恰好反映了网络的社区边界。
意义：可以通过跟踪渗流过程来探测网络的社区结构，为理解网络内部结构提供了新工具。

3. 基础设施网络：级联失效与相依网络

背景：2003年意大利电网与信息网耦合导致的级联失效事件。
模型：Buldyrev 等人 (2010) 提出相依网络模型。
发现：
- 两个相互依赖的随机网络，其级联失效过程表现为爆炸渗流，即一旦开始失效，系统会突然崩溃（一阶相变）。
- 耦合强度影响相变类型：降低耦合强度可使相变从一阶转变为连续。
- 更现实的模型中（同时存在依赖边和连接边），会出现混合相变：先有一个不连续的跳跃，随后缓慢连续下降。
意义：揭示了关键基础设施系统的脆弱性根源，并为设计更鲁棒的耦合系统提供了理论依据。