【深度学习】深度学习核心：优化与正则化超详细笔记

深度学习核心：优化与正则化超详细笔记（附图解）

本笔记基于南方科技大学张建国教授的《Deep Learning (CS324)》课程第五讲内容，该课程主要参考Ian Goodfellow等人的《Deep Learning Book》第7、8章。本文旨在为初学者提供一份关于深度学习优化与正则化的全面、易懂的学习指南。

前言：为什么优化与正则化如此重要？

想象一下，训练一个深度学习模型就像是在一个巨大、黑暗且地形复杂的山谷里寻找最低点（即损失函数的最小值）。

• 优化 就像是你的 寻路策略。你是选择一步看一步（随机梯度下降），还是先观察整个山谷的地形再行动（批量梯度下降）？你是直来直去，还是借助惯性（动量）更快地滑行？
• 正则化 则像是给你的 寻路装备增加约束。为了防止你只在训练走过的小路上表现优异（过拟合），你需要一些方法让自己变得更“皮实”，能适应各种未知的路况（泛化能力）。
  掌握好这两者，是训练出高性能深度学习模型的关键。

---

一、梯度下降的三兄弟：批量、随机与小批量

梯度下降是优化算法的基石，但它并非只有一种形式。根据每次更新参数时使用的数据量不同，可以分为三种主要类型。

1.1 批量梯度下降(Batch Gradient Descent)

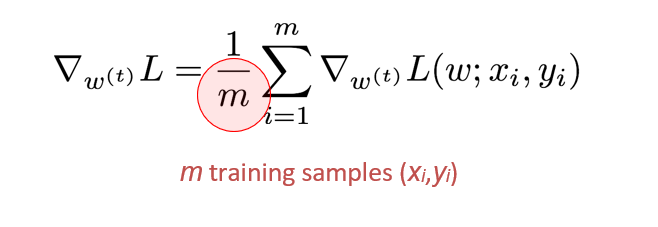
核心思想：每次更新参数时，都使用整个训练集来计算损失和梯度。
计算过程：

1. 将所有 m 个训练样本 (x_i, y_i) 输入网络。
2. 计算所有样本的平均损失 J(θ)。
3. 计算这个总损失关于模型参数 θ 的梯度 ∇J(θ)。
4. 用这个梯度更新所有参数：θ = θ - η * ∇J(θ)。
   优点：

• 收敛路径稳定：由于每次都考虑了所有数据，梯度方向准确，下降路径平稳，不会剧烈震荡。
• 理论保证：对于凸函数，保证能找到全局最优解。
  缺点：
• 计算成本极高：当数据集非常大时（百万、千万级别），计算一次完整梯度需要耗费大量时间和内存，可能不切实际。
• 容易陷入局部最优：在非凸的深度学习损失面上，稳定的梯度可能会使其陷入某个局部最小值或鞍点，难以跳出。

生活比喻：好比你要决定整个城市最受欢迎的餐厅。你调查了城市里每一个人的意见，然后才做出决定。这个决定非常准确，但耗时耗力。

1.2 随机梯度下降

核心思想：每次更新参数时，只随机选择一个训练样本来计算损失和梯度。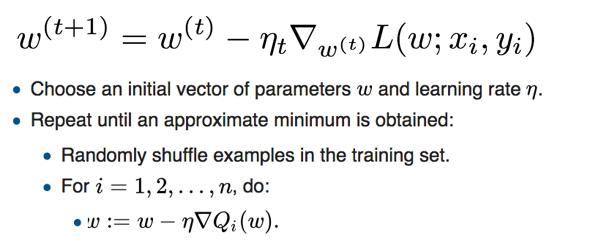

计算过程：

1. 从训练集中随机抽取一个样本 (x_i, y_i)。
2. 计算这个样本的损失 J(θ; x_i, y_i)。
3. 计算该样本的梯度 ∇J(θ; x_i, y_i)。
4. 立即更新参数：θ = θ - η * ∇J(θ; x_i, y_i)。
5. 重复以上步骤，直到遍历完所有样本（完成一个epoch）。
   优点：

• 更新速度快：每一步计算量极小，能快速开始学习。
• 有助于跳出局部最优：单样本的梯度带有很大的随机性（噪声），这种噪声虽然让下降路径看起来“醉汉走路”，但却能帮助模型“冲”出局部最小值和鞍点。
• 适合在线学习：对于数据流式到来的场景（如实时推荐），SGD可以即时更新模型。
  缺点：
• 收敛不稳定：高方差导致更新过程震荡剧烈，损失函数下降曲线毛刺很多。
• 无法充分利用并行计算：一次只处理一个样本，无法发挥GPU等硬件的并行计算优势。

生活比喻：还是决定餐厅，你这次只问了街边随机遇到的一个人的意见，然后就立刻更新你的“最佳餐厅”排名。你的排名变化很快，但可能很不稳定，容易受极端个例影响。

1.3 小批量梯度下降

核心思想：这是BGD和SGD的折中方案，也是目前深度学习领域的标准做法。每次更新参数时，使用一小批（mini-batch）数据。
计算过程：

1. 从训练集中随机抽取一小批 B 个样本（B 通常是32, 64, 128…）。
2. 计算这批样本的平均损失 J(θ; x_(i:i+B), y_(i:i+B))。
3. 计算该批次的梯度 ∇J(θ; x_(i:i+B), y_(i:i+B))。
4. 更新参数：θ = θ - η * ∇J(θ; x_(i:i+B), y_(i:i+B))。
   优点：

• 兼顾了效率和稳定性：相比BGD，计算量大幅下降；相比SGD，每次更新都参考了多个样本，梯度方向更稳定，降低了方差。
• 充分利用硬件并行性：批量大小 B 可以很好地适配GPU内存，实现高效并行计算。
  缺点：
• 引入了一个新的超参数：批量大小 B 的选择需要经验。太小则不稳定，太大则接近BGD且消耗内存。通常的选择是“尽可能大，只要GPU内存放得下”。

生活比喻：你这次决定问**一小群人（比如一个办公室的同事）**的意见。这个决定比问一个人要稳定，比问全城人要高效，是现实中最好的策略。

---

二、优化路上的“拦路虎”：挑战与对策

即使有了梯度下降，训练过程也并非一帆风顺。我们会遇到各种棘手的“地形”。

2.1 病态条件

问题描述：损失函数在某些方向上非常陡峭，而在另一些方向上非常平缓，形成一个狭长的山谷。
影响：梯度下降会在陡峭的墙壁之间来回震荡，进展缓慢，难以沿着平缓的方向直达谷底。
对策：后面会讲到的动量法和自适应学习率方法能有效缓解这个问题。

2.2 局部最小值、鞍点与平台区

• 局部最小值：一个“小坑”，不是全局最低点。
• 鞍点：一个“马鞍”形状，在某些方向是最小值，在另一些方向是最大值。在高维空间中，鞍点比局部最小值更常见。
• 平台区：梯度接近于零的平坦区域，模型学习停滞。
  影响：标准梯度下降可能会在这些区域“卡住”，因为梯度太小或为零，无法继续前进。
  对策：SGD的随机性本身就是一种对策，噪声可以帮助模型“跳”出这些区域。此外，动量法也能凭借惯性冲过平缓区域。
  

2.3 悬崖与梯度爆炸

问题描述：参数空间中某些区域，损失函数会发生突变，形成一个“悬崖”。
影响：当梯度计算点靠近悬崖时，梯度值会变得异常巨大，导致参数更新步长过大，可能直接“飞”到参数空间的一个糟糕位置，甚至导致数值溢出（NaN）。
对策：梯度裁剪是一种常用技术，即设定一个梯度的阈值，当梯度的范数超过这个阈值时，就将其缩放到阈值大小。

三、给优化器装上“加速器”：动量法

为了克服上述挑战，特别是震荡和平台区问题，我们引入了动量法。

3.1 标准动量

核心思想：借鉴物理学中的动量概念。在更新参数时，不仅考虑当前梯度，还要保留一部分历史更新方向。
类比：想象一个球从山上滚下。如果它只受当前坡度（梯度）的影响，可能会在狭窄的山谷里来回震荡。但如果它有惯性（动量），它会积累之前的速度，更容易冲过震荡区域，更快地滚向谷底。
公式：

1. v_t = γ * v_{t-1} + η * ∇J(θ) （更新速度）
2. θ = θ - v_t （用速度更新位置）

• v_t 是当前时刻的“速度”向量。
• v_{t-1} 是上一时刻的速度。
• γ 是动量系数（通常取0.5, 0.9, 0.99），控制历史动量的保留程度。γ 越大，惯性越强。
• η 是学习率。
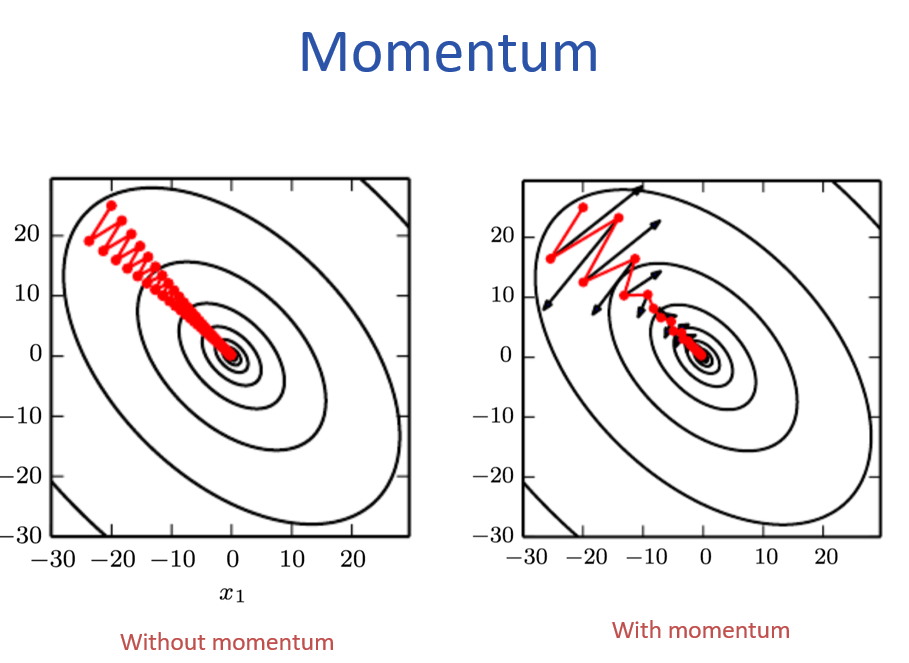
  效果：
• 加速收敛：在梯度方向一致的方向上，动量会累积，加速前进。
• 抑制震荡：在梯度方向反复变化的方向上，动量会相互抵消，减小震荡。

图：无动量（左）震荡剧烈，有动量（右）能有效抑制震荡并加速 [图源：PPT]

3.2 Nesterov 加速梯度

核心思想：标准动量的一个“ lookahead”改进版本。它在计算当前梯度之前，先根据历史动量“试探性地”向前走一步，然后在那个“未来位置”计算梯度并修正。
公式：

1. v_t = γ * v_{t-1} + η * ∇J(θ - γ * v_{t-1}) （在“未来位置”计算梯度）
2. θ = θ - v_t
   优势：Nesterov动量对未来的梯度有了一定的预判，使得更新方向更准确，收敛通常比标准动量更快、更稳定。

---

四、自适应学习率：每个参数都有自己的“学习节奏”

全局学习率 η 对所有参数一视同仁，但这往往不是最优的。有些参数需要大步快跑，有些则需要小步慢走。自适应学习率方法应运而生。

4.1 AdaGrad (Adaptive Gradient)

核心思想：为每个参数维护一个累积的历史梯度平方和。梯度越大的参数，其学习率会自动变得越小；反之亦然。
公式：

1. G_t = G_{t-1} + (∇J(θ))^2 （累积梯度平方）
2. θ = θ - η / (√G_t + ε) * ∇J(θ) （用累积梯度缩放学习率）

• G_t 是一个对角矩阵，存储了每个参数到当前时刻为止的梯度平方和。
• ε 是一个很小的数（如1e-8），为了防止除以零。
  优点：无需手动调学习率，能自动适应不同参数。
  缺点：G_t 是单调递增的，导致学习率会不断衰减，最终可能变得非常小，导致模型提前停止学习。

4.2 RMSprop (Root Mean Square Propagation)

核心思想：这是对AdaGrad的改进。它不再累积所有历史梯度，而是使用一个指数移动平均来计算梯度的平方均值。这使得算法只关注最近一段时间的梯度情况。
公式：

1. E[g^2]_t = β * E[g^2]_{t-1} + (1-β) * (∇J(θ))^2 （计算梯度平方的指数移动平均）
2. θ = θ - η / (√E[g^2]_t + ε) * ∇J(θ)

• β 是衰减率（通常取0.9），控制历史信息的保留程度。
  优点：解决了AdaGrad学习率单调递减的问题，非常适合非凸优化，是深度学习中非常流行的算法。

4.3 Adam (Adaptive Moment Estimation)

核心思想：集大成者，可以看作是 RMSprop + Momentum 的结合体。它同时为每个参数维护了梯度的一阶矩（均值，类似动量）和二阶矩（方差，类似RMSprop）。
公式：

1. m_t = β1 * m_{t-1} + (1-β1) * ∇J(θ) （一阶矩估计，即动量）
2. v_t = β2 * v_{t-1} + (1-β2) * (∇J(θ))^2 （二阶矩估计，即RMSprop）
3. m̂_t = m_t / (1 - β1^t) （修正一阶矩的偏差）
4. v̂_t = v_t / (1 - β2^t) （修正二阶矩的偏差）
5. θ = θ - η / (√v̂_t + ε) * m̂_t （更新参数）

• β1 通常取0.9，β2 通常取0.999。
• 步骤3和4是为了在训练初期修正偏差，因为 m_t 和 v_t 初始化为0。
  优点：
• 结合了动量和RMSprop的优点：既有惯性加速，又有自适应学习率。
• 鲁棒性强：对超参数的选择不那么敏感，通常使用默认值就能取得不错的效果。
• 收敛速度快：在大多数情况下是首选的优化算法。

总结与选择：

• 初学者/快速原型：直接用 Adam，简单有效。
• 追求最佳性能：可以尝试 SGD + Momentum，并配合精良的学习率衰减策略，有时能获得比Adam更好的最终结果。
• RMSprop 也是一个非常可靠的选择，特别是在某些RNN任务中。

---

五、防止模型“死记硬背”：正则化技术

当模型过于复杂时，它可能会“记住”训练数据的所有细节和噪声，而不是学习其内在规律，这就是过拟合。正则化技术通过限制模型的复杂度来防止过拟合。

5.1 L1 与 L2 正则化

核心思想：在损失函数后面加上一个惩罚项，惩罚模型中过大的权重。
L2 正则化（权重衰减, Weight Decay）：

• 惩罚项：λ * Σ w_i^2 （λ 是正则化强度）
• 效果：让模型的权重尽可能小，但不会变为0。这会使模型更平滑，倾向于使用所有输入特征，但给不重要的特征较小的权重。
• 更新规则：θ = θ - η * ∇J(θ) - η * λ * θ，可以看到，每次更新都会让权重 θ 乘以一个略小于1的因子 (1 - η * λ)，这就是“权重衰减”的由来。
  L1 正则化：
• 惩罚项：λ * Σ |w_i|
• 效果：倾向于让不重要的权重精确地变为0。这使得模型变得稀疏，相当于自动进行了特征选择，只保留了最重要的特征。
• 为什么能产生稀疏性？：L1惩罚项的导数是常数（λ * sign(w)），无论权重多小，惩罚力度都一样，这会推动权重一直减小直到变成0。
  | 特性 | L2 正则化 | L1 正则化 |
  |—|—|—|
  | 惩罚项 | λ * Σ w² | λ * Σ |w| |
  | 权重效果 | 权重趋近于0（但不为0） | 权重变为0（稀疏） |
  | 适用场景 | 通用，防止过拟合 | 需要特征选择，希望模型稀疏 |

5.2 数据增强

核心思想：与其限制模型，不如给它“看”更多的数据。当训练数据有限时，我们可以通过对现有数据进行各种变换，创造出“新”的数据。
常见方法：

• 图像：随机裁剪、旋转、翻转、颜色抖动、添加噪声等。
• 文本：同义词替换、回译（翻译成另一种语言再翻译回来）等。
  效果：模型能学习到数据的不变性（比如，猫不管正着放还是倒着放都是猫），从而大大提升泛化能力。

5.3 早停

核心思想：一个非常简单但极其有效的正则化方法。在训练过程中，同时监控模型在训练集和验证集上的性能。
实施步骤：

1. 每个epoch结束后，计算验证集上的误差（或准确率）。
2. 只要验证集误差持续下降，就继续训练。
3. 当验证集误差连续多次不再下降，甚至开始上升时，就停止训练。
4. 保存验证集性能最好的那个时刻的模型参数。
   效果：在模型刚刚开始过拟合（即开始“死记硬背”训练数据）的时候及时刹车，防止其走得太远。

5.4 Dropout

核心思想：一种在训练期间“随机失活”神经元的正则化技术。
实施步骤：

1. 在训练的每次迭代中，以概率 p 随机地选择一部分神经元，将其输出暂时置为0。
2. 前向传播和反向传播都只在剩下的神经元网络中进行。
3. 在测试时，所有神经元都参与工作，但它们的输出需要乘以 p（或者说，在训练时将存活神经元的输出除以 p），以补偿训练时被丢弃的神经元。
   效果：

• 集成学习的近似：每次迭代都在训练一个不同的“子网络”，最终模型相当于大量子网络的集成，增强了鲁棒性。
• 强制神经元学习冗余表示：由于不知道哪个神经元会被丢弃，每个神经元都不能依赖于其他特定的神经元，必须学习到更有用的特征。
• 有效防止过拟合：是深度学习中最常用的正则化手段之一。

---

六、训练的“起手式”：参数初始化与数据预处理

好的开始是成功的一半。正确的参数初始化和数据预处理能让训练事半功倍。

6.1 权重初始化

为什么重要？：如果所有权重都初始化为同一个值（比如0），那么同一层的所有神经元在反向传播时会接收到完全相同的梯度，从而进行完全相同的更新。这会导致“对称性”问题，使得所有神经元学到的东西都一样，网络失去了学习能力。
原则：需要打破对称性，让权重具有随机性，同时要控制好权重的尺度。
常用方法：

• Xavier/Glorot 初始化：适用于 tanh 和 sigmoid 激活函数。它根据输入和输出的神经元数量来初始化权重，旨在让各层输入和输出的方差保持稳定。
  • 权重从 [-√(6/(m+n)), √(6/(m+n))] 的均匀分布中采样，其中 m 是输入单元数，n 是输出单元数。
• He 初始化：适用于 ReLU 及其变体。考虑到 ReLU 会使一半的神经元输出为0，He初始化的方差是Xavier的两倍。
  • 权重从均值为0，方差为 2/m 的正态分布中采样。

6.2 数据预处理

目标：让输入数据更适合模型处理。
常用方法：

• 零中心化：对每个特征维度，减去其均值。使得数据以0为中心分布。
• 归一化：将数据缩放到相似的尺度。最常见的是将每个特征除以其标准差，使其变为标准正态分布（均值为0，方差为1）。
  为什么重要？：如果不同特征的尺度差异巨大（比如一个特征是0-1，另一个是0-10000），那么梯度下降的路径会变得非常扭曲，收敛缓慢。归一化能让损失函数的等高线图更接近圆形，便于优化。

6.3 批量归一化

核心思想：这是一个革命性的技术，它将数据预处理的思想应用到了网络的每一层。
问题：在深度网络中，随着参数的更新，每一层输入的分布会不断发生变化，这被称为“内部协变量偏移”。这使得每一层都需要不断去适应新的输入分布，减慢了训练速度。
解决方法：在网络的每一层（通常是激活函数之前）都进行一次归一化。
操作步骤：

1. 对于一个mini-batch的数据，计算其均值 μ_batch 和方差 σ²_batch。
2. 对该批数据进行归一化：x̂ = (x - μ_batch) / √(σ²_batch + ε)。
3. 对归一化后的数据进行缩放和平移：y = γ * x̂ + β。其中 γ 和 β 是可学习的参数，让网络可以恢复出原始数据分布（如果需要的话）。
   惊人效果：

• 允许使用更大的学习率：加速训练。
• 减少对初始化的依赖：即使初始化不那么好，BN也能帮助稳定训练。
• 轻微的正则化效果：由于每个batch的均值和方差是由该batch数据计算得出的，引入了噪声，有类似Dropout的效果。
• 缓解梯度消失/爆炸问题。

---

七、总结

训练一个深度学习模型，就像是一门艺术与科学的结合。我们需要：

1. 选择一个合适的优化器：从 Adam 开始，它是稳健的基线；若追求极致性能，可尝试 SGD with Momentum 配合学习率调度。
2. 应用正则化：Dropout 和 L2 正则化 是标配；数据增强 是提升性能的免费午餐；早停 是防止过拟合的保险。
3. 做好准备工作：使用 Xavier 或 He 初始化；对输入数据进行零中心化和归一化；在模型中加入 批量归一化 层，几乎总能带来提升。
   这些技术不是孤立的，而是相辅相成的。理解它们的原理，并在实践中不断尝试和组合，是通往深度学习高手的必经之路。希望这份详细的笔记能为你打下坚实的基础！