当前位置：首页 > news >正文

查错控制方法-上（奇偶校验与循环冗余校验）

news 2025/10/25 12:14:40

概念

差错控制是数据通信和网络传输中的关键技术，旨在检测和纠正数据传输过程中因噪声、干扰或信号衰减导致的错误。

在数据链路层广泛地采用了编码技术来实现差错控制。编码技术主要有两类：

前向纠错技术：接收端接收到有差错的数据帧时，能够自动根据冗余码将差错改正过来，但这种方式开销较大，不适合计算机通信。
检错重发方式：接收端可以根据冗余码检测出收到的帧中是否有错误，但具体不知道哪里出错，而是让发送端重复发送该帧，直到被正确接收，但重传次数也是有限制的，当重传多次失败，会作为不可恢复故障向上层（网络层）报告，这种方式是计算机通信中最常用的。

常见的差错控制方法有：奇偶校验码、循环冗余编码、海明码和自动重传请求。（本文先对前两个进行讲解，后两个放在下一篇文章再来详细讲解）

奇偶校验码

一维奇偶校验码

奇偶校验码是一种最基本、最常用和最简单的检错码。

规则：在信息码的后面附加一个校验位，使得码组中 ‘1’ 的个数是奇数或偶数；在接收端再检测 ‘1’ 的个数，判断是否与发送端相同来判断是否出现错误。

若传输信息有n-1个码元： $C_{n-1}...... C_2 C_1$ ，校验位为 $C_0$ ，则

奇校验方程： $C_{n-1}\oplus......\oplus C_2 \oplus C_1\oplus C_0=1$ ；

偶校验方程： $C_{n-1}\oplus......\oplus C_2 \oplus C_1\oplus C_0=0$ 。

注意：

不管信息位有多少位，校验位只有一位（0或1），如果它使信息码中 ‘1’ 的个数为偶数，则为偶校验；如果它使信息码中 ‘1’ 的个数为奇数，则为奇校验。
接收端通过对收到的信息码进行模2加运算（异或运算：异为1（ $1\oplus0=1;0\oplus1=1$ ），同为0（ $0\oplus0=0;1\oplus1=0$ ））来判断。
奇偶校验能查出传输过程中任意奇数个错误，但不能发现偶数个错误。

发送端：发送数据为：1001
使用奇校验可得到待传输的数据为：1001(1)
若接收端收到10011： $1 \oplus 0\oplus 0\oplus 1\oplus 1=1$ ，符合奇校验，认为传输过程没有出错；
若接收端收到10010： $1 \oplus 0\oplus 0\oplus 1\oplus 0=0$ ，不符合奇校验，认为传输过程中出错了；
若接收端收到00010： $0 \oplus 0\oplus 0\oplus 1\oplus 0=1$ ，符合奇校验，认为传输过程没有出错，但实际上已经出错了。

二维奇偶校验（用得较少，了解即可）

垂直奇偶校验

规则：把要发送的信息码元按定长m比特（m通常取8，即一个字符长度，故也称字符奇偶校验）分为若干段，每段纵向排列，对每列信息元进行奇偶校验，将校验位附在每列后面，传输时按列的次序传输。

注意：

校验位单独集中放在最后，不插在各自列的末尾。
只能查出垂直列上的奇数位差错，校验不出偶数位差错。

传送信息码：1011111110010001000111000，取定长m=5，则序列可分为5段（纵向排列）：10111，11110，01000，10001，11000，选择偶校验（纵向）
组别信息元
1 1 1 0 1 1
2 0 1 1 0 1
3 1 1 0 0 0
4 1 1 0 0 0
5 1 0 0 1 0
校验位 0 0 1 0 0
由表可得到传输序列：10111 11110 01000 10001 11000 00100。

组别	信息元
1	1	1	0	1	1
2	0	1	1	0	1
3	1	1	0	0	0
4	1	1	0	0	0
5	1	0	0	1	0
校验位	0	0	1	0	0

水平奇偶校验

规则：把要发送的信息码元按定长m比特分为若干段，每段横向排列，对每行信息元进行奇偶校验，将校验位附在每行后面，传输时仍然按列的次序传输。

传送信息码：1011111110010001000111000，取定长m=5，则序列可分为5段（纵向排列）：10111，11110，01000，10001，11000，选择偶校验（横向）
组别信息元校验元
1 1 1 0 1 1 0
2 0 1 1 0 1 1
3 1 1 0 0 0 0
4 1 1 0 0 0 0
5 1 0 0 1 0 0
由表可得到传输序列：10111 11110 01000 10001 11000 01000。

组别	信息元	校验元
1	1	1	0	1	1	0
2	0	1	1	0	1	1
3	1	1	0	0	0	0
4	1	1	0	0	0	0
5	1	0	0	1	0	0

水平垂直奇偶校验

规则：把前两种校验规则结合起来（这里就不举例子了）

循环冗余编码

循环冗余校验码（Cyclic Redundancy Check，CRC），又称多项式码，是一种计算机网络和数据通信使用最广泛的检错码，它是在严格的数学基础上建立起来的，检错能力非常强，而且只要用一个简单的电路（异或门）即可实现。

基本思想：给定一个m位比特的帧或信息，发送端产生一个r比特校验位，称为帧序列FCS，使得这个m+r比特组成的码字可被某个预定的整数相除；接收端将收到的码字除以相同的数，当没有余数时，认为没有错误。

规则：设原始数据帧M’，m为M的位数，除数G（是一个多项式，称为生成多项式，其中，r为G的多项式的最高次幂），被除数M（由r和M共同得出：r有几位，则在M‘后补r个0），对其进行模2除运算（做减法不产生借位，加法不产生进位，其实就是异或运算），最后产生的余数就是帧序列，将待传输数据帧与FCS拼接在一起就形成了CRC码。

待传输数据M’=101001， $G(x)=x^3+x^2+1$ ，1、求帧序列FCS和CRC码。2、接收端怎么检错。
解：
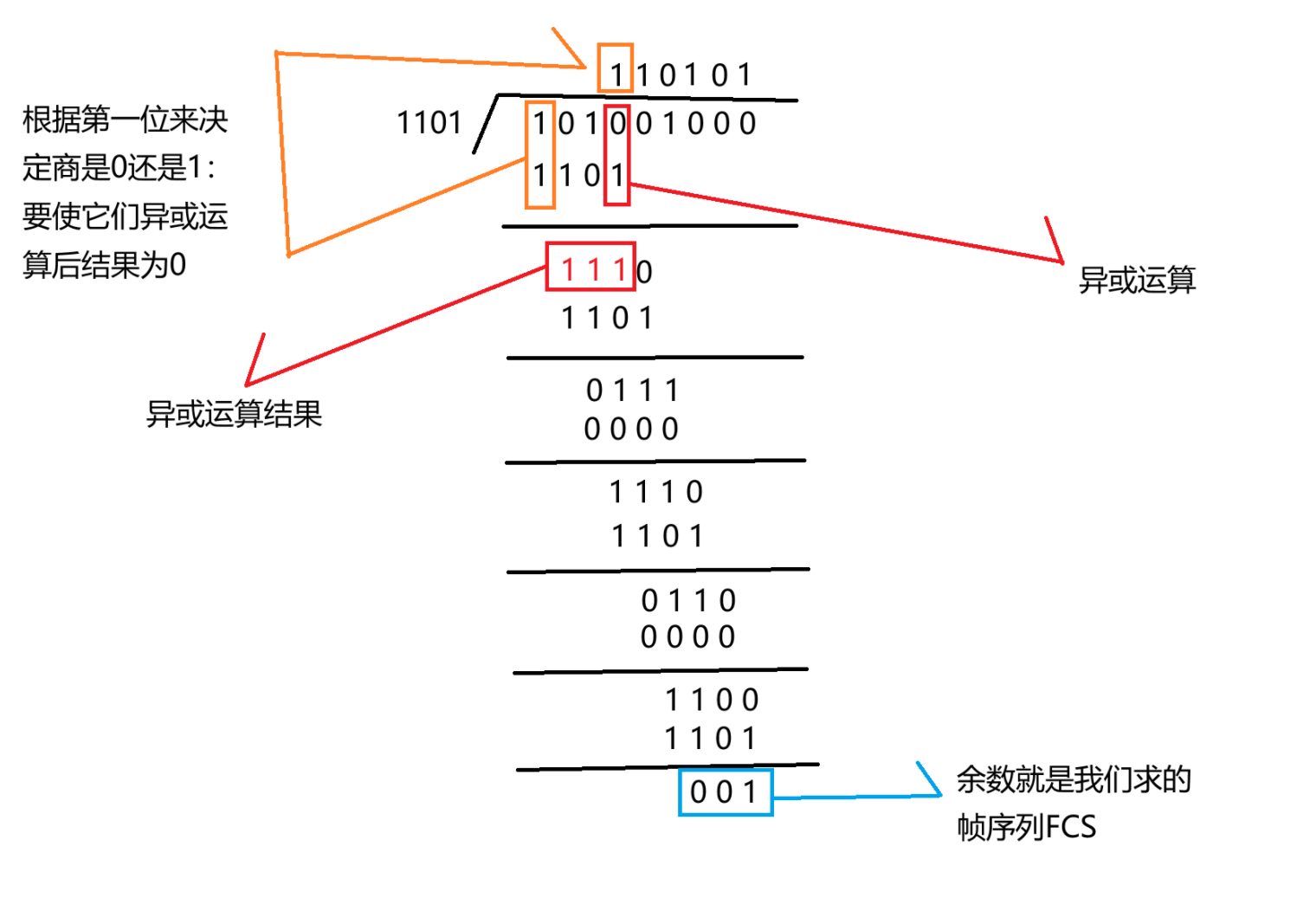
1、由题知：G=1101（最高位是3，从0-3共4位，有值的项为1，无值的项为0），r=3；因此，被除数M=101001000
运算过程：
所以，求得的帧序列FCS为001（3位，位数与r相同）；故CRC码为：101001001（将FCS拼接到原始数据帧后，其作为传输序列，会发送给接收端）。
2、对接收到的数据进行模2除运算，根据余数判断：
假设未发生错误：接收端接收到的CRC码为：101001001，用G(x)进行模2除，余数为000（可以自己代入上方计算过程验证一下，这里就不列出来了，操作过程是一样的），因此，该数据帧传输过程中未出现差错；
假设第6位发生错误：接收端接收到的CRC码为：101101001，用G(x)进行模2除，余数为011，不为0，因此，认为在传输过程中发生错误。

在上面我们可以发现，第6位发生错误时，余数正好是011，换算为10进制正好是6，是不是CRC编码还有纠错功能？对的，不过是有条件的。
假如CRC=110110，G=101，有
接收到的CRC 余数出错位
110110 00 无
110111 01 1
110100 10 2
110010 01 3
111110 10 4
100110 01 5
010110 10 6
我们可以发现，它的余数其实是一直在循环出现的（这应该就是它的名字的由来），在这里，就无法纠错了。
因此，帧序列FCS有r位，其中0表示没有差错，有 $2^r-1$ 个可表示出错位，传输的CRC有m+r位，故，只有当 $2^r\geq m+r+1$ 时，才可以进行一位的纠错，但实际中，m相比r可能大得多，用来纠错不切实际，因此，CRC编码一般不用来纠错，只用来检错。