东营网站app建设周杰伦做的广告网站
第四章:定位滤波器
欢迎回来,充满抱负的机器人专家~
在第一章:机器人状态/位姿中,我们学习了机器人如何跟踪自身身份:位置、朝向和速度。在第二章:环境表示(栅格地图)中,我们了解了机器人如何理解周围世界。在第三章:机器人运动模型中,我们探索了机器人如何根据自身运动预测未来位置。
现在,假设我们的清洁机器人从(0,0)位置开始工作,知道自身速度,并利用运动模型预测路径。它预测经过特定时间后将到达(1.0, 0.0)。完美!
但如果轮子发生微小打滑呢?或者地面不完全平坦?或者电机出力与预期存在偏差?
即使运动预测中的微小误差,随时间累积也会导致机器人严重偏离实际位置,这种现象称为航位推测漂移。这就像仅通过步数计数和转向来导航城市,却从不查看地图或路标,最终必定迷路!
这时就需要定位滤波器登场!
什么是定位滤波器?
定位滤波器是一种智能算法,帮助机器人确定自身在环境中的真实位置和朝向(即第一章的x、y、yaw和v)。它如同机器人的内置GPS系统,持续自问:“我现在究竟身处何处?”
其原理是巧妙融合两大信息源:
- 运动模型预测:基于运动指令的机器人预期位置(参见第三章:机器人运动模型)
- 传感器测量:通过传感器(如GPS、激光雷达、摄像头或轮式编码器)获取的实际环境观测数据
滤波器的工作是将运动模型的最佳预测与现实传感器数据结合,持续更新更精确的位置估计,从而消除导致航位推测漂移的微小误差。
核心理念:预测与更新
所有定位滤波器,无论复杂度如何,都遵循基本的两步循环:
| 步骤 | 描述 | 类比 |
|---|---|---|
| 1. 预测 | 使用机器人运动模型,根据控制指令计算机器人预期的下一位置 | 闭眼前行时,预测自己将到达的位置 |
| 2. 更新 | 获取新传感器测量值。滤波器将实际测量值与预测值对比,利用差异修正位置估计 | 睁眼发现偏离预期位置,据此调整内部地图 |
这个"预测-更新"循环每秒重复多次,使机器人能持续精化对自身位置的理解。
如何使用定位滤波器
PythonRobotics包含多种定位滤波器,如扩展卡尔曼滤波器(EKF)、无迹卡尔曼滤波器(UKF)、粒子滤波器和直方图滤波器。
它们都执行"预测-更新"循环,但采用不同数学方法处理不确定性。
让我们以**扩展卡尔曼滤波器(EKF)**为例,这是种常见且强大的技术。核心逻辑通常封装在类似ekf_estimation的函数中。
以下是调用EKF的简化示例:
import numpy as np# 假设这些变量已在其他地方定义(例如EKF文件中)
# xEst: 当前最优状态估计 [x, y, yaw, v]
# PEst: 状态估计的不确定性(协方差矩阵)
# z: 实际传感器测量值(如GPS坐标 [x_gps, y_gps])
# u: 控制输入(如[速度指令, 偏航率指令])# 初始估计和不确定性
xEst = np.array([[0.0], [0.0], [0.0], [0.0]]) # 机器人认为自己在原点
PEst = np.eye(4) * 0.1 # 初始较小不确定性# 循环中每个时间步:
# 1. 获取新控制输入和传感器测量
u_current = np.array([[1.0], [0.1]]) # 以1m/s前进,0.1 rad/s转向
z_current = np.array([[0.1], [0.0]]) # GPS显示(0.1, 0.0)# 2. 调用定位滤波器函数
# (函数内部执行预测和更新步骤)
# xEst_new, PEst_new = ekf_estimation(xEst, PEst, z_current, u_current)# print(f"新估计X坐标: {xEst_new[0,0]:.2f}")
# print(f"新估计Y坐标: {xEst_new[1,0]:.2f}")
参数说明:
xEst(估计状态):滤波器对机器人x、y、yaw和v的最佳当前估计PEst(估计协方差):表征对xEst的置信度矩阵。小值表示高置信,大值表示低置信z(观测值):来自传感器的原始数据(如GPS的x、y坐标)u(控制输入):发送给机器人的指令,由运动模型用于预测
ekf_estimation函数(或其他滤波器的类似函数)接收这些输入,内部执行预测和更新步骤,输出精化的新xEst和PEst。
定位滤波器内部工作原理(EKF示例)
通过序列图可视化"预测-更新"循环:
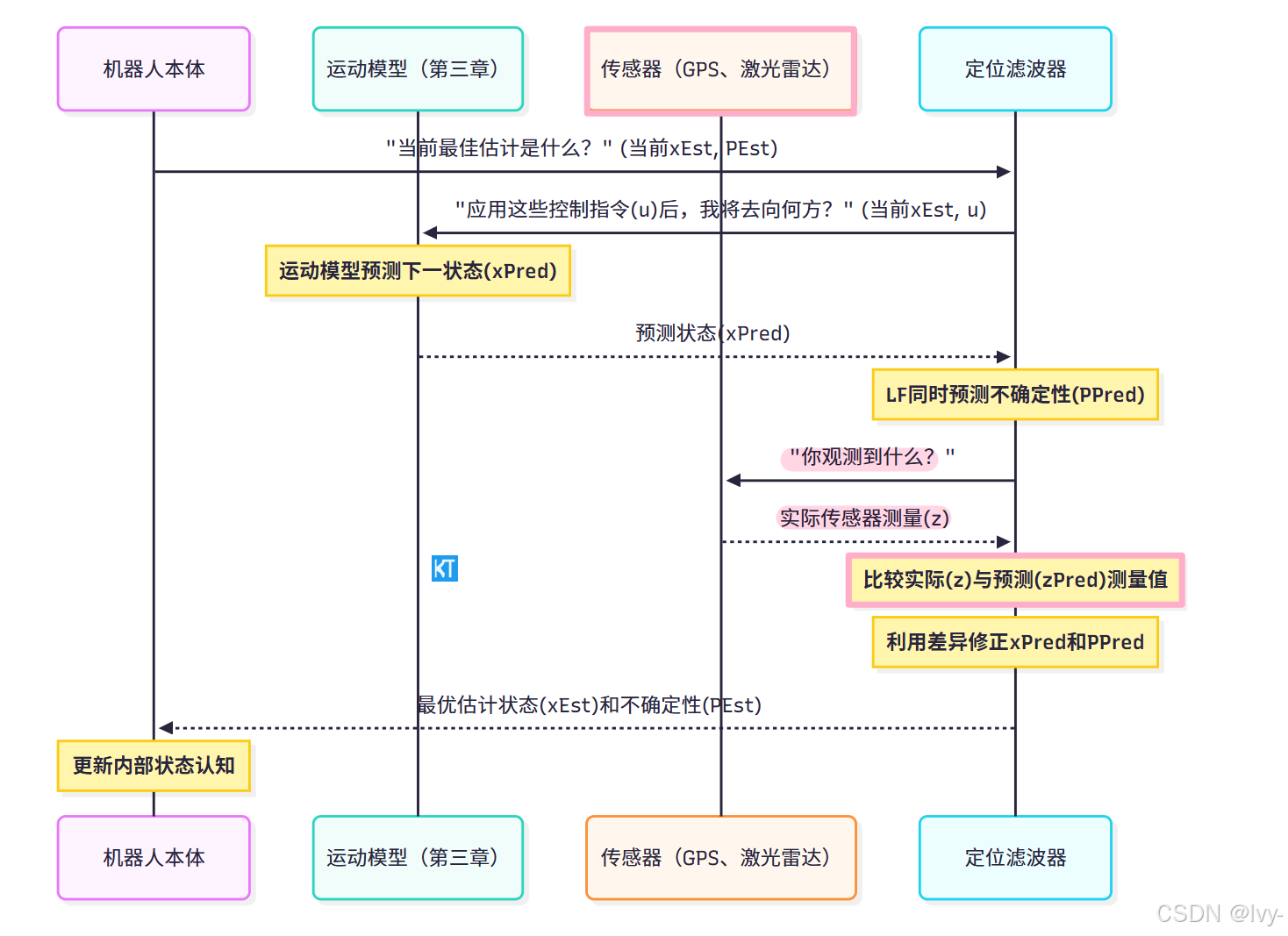
现在查看Localization/extended_kalman_filter/extended_kalman_filter.py中的简化代码片段:
import numpy as np
import math# 假设DT(时间步长)已定义,例如DT=0.1# 简化的motion_model和observation_model(来自文件)
def motion_model(x, u):# 类似于第三章的update_motion_model# 根据当前状态x和控制u预测DT时间后的状态# (实际实现涉及矩阵运算,此为概念演示)x_new = np.copy(x) # 复制当前状态v = u[0, 0] # 速度指令yaw_rate = u[1, 0] # 偏航率指令# 状态预测(简化运动学模型)x_new[0, 0] += v * math.cos(x[2, 0]) * DT # 新x坐标x_new[1, 0] += v * math.sin(x[2, 0]) * DT # 新y坐标x_new[2, 0] += yaw_rate * DT # 新偏航角x_new[3, 0] = v # 新速度(直接采用指令)return x_newdef observation_model(x):# 预测在状态x时应有的传感器读数# 对于简单GPS,仅提取x和y坐标z_pred = np.array([[x[0, 0]], [x[1, 0]]]) # 从状态预测x,yreturn z_pred# --- 核心EKF估计函数 ---
def ekf_estimation(xEst, PEst, z, u):# 1. 预测步骤xPred = motion_model(xEst, u) # 使用运动模型预测状态# jF = jacob_f(xEst, u) # (简化处理:忽略运动模型雅可比矩阵)# PPred = jF @ PEst @ jF.T + Q # 预测不确定性增长(含过程噪声Q)PPred = PEst # 极大简化:假设不确定性不增长# 2. 更新步骤(校正)# jH = jacob_h() # (简化处理:忽略观测模型雅可比矩阵)zPred = observation_model(xPred) # 预测在xPred时应有的观测值y = z - zPred # "创新"或测量误差:实际与预测之差# S = jH @ PPred @ jH.T + R # (简化处理:忽略含测量噪声R的协方差计算)# K = PPred @ jH.T @ np.linalg.inv(S) # (简化处理:忽略卡尔曼增益计算)# 使用误差和卡尔曼增益(K)校正状态估计# xEst = xPred + K @ yxEst = xPred + y # 极大简化:直接应用校正# 更新不确定性(PEst)# PEst = (np.eye(len(xEst)) - K @ jH) @ PPredPEst = PPred # 极大简化:保持不确定性不变return xEst, PEst
EKF在PythonRobotics中的实现解析:
xEst和PEst:滤波器对机器人状态及其不确定性的当前认知motion_model(xEst, u):即第三章的机器人运动模型,基于当前最优估计和控制输入预测理想状态xPredjacob_f和Q:EKF预测步骤还估计不确定性PEst的增长。jacob_f(运动模型雅可比矩阵)描述状态变化对运动的影响,Q(过程噪声协方差)表征运动模型自身的不确定性(如轮子打滑)observation_model(xPred):基于预测状态xPred,预测传感器应有的读数zPredz - zPred:关键差异!传感器实际读数z与预测读数zPred的差值构成"误差"或"创新",用于校正估计jacob_h和R:jacob_h(观测模型雅可比矩阵)描述状态变化对观测的影响,R(测量噪声协方差)表征传感器噪声(如GPS信号干扰)- 卡尔曼增益(
K):卡尔曼滤波器的核心参数,决定信任传感器测量还是预测的程度。传感器噪声大时K较小(更信预测),预测不确定性大时K较大(更信测量) xEst = xPred + K @ y:更新方程,新最优估计是预测状态与加权校正项之和PEst更新:更新后的协方差矩阵通常缩小,反映融合新测量后的置信度提升
PythonRobotics中的其他定位滤波器
除EKF外,项目还展示多种滤波器适应不同场景:
- 粒子滤波器(
Localization/particle_filter/particle_filter.py):维护多个"粒子"表示可能位置,通过观测数据加权和重采样更新粒子分布,适合复杂环境(如对称空间)的多模态定位 - 无迹卡尔曼滤波器(UKF)(
Localization/unscented_kalman_filter/unscented_kalman_filter.py):使用"sigma点"准确捕捉非线性变换,相比EKF的线性化近似,UKF在强非线性问题中精度更高但计算量更大 - 直方图滤波器(
Localization/histogram_filter/histogram_filter.py):将环境划分为栅格(类似第二章的栅格地图),计算各栅格概率,通过概率转移和乘法更新,适合二维栅格环境下的直观定位
这些滤波器使用不同数学工具解决同一核心问题——确定机器人位置,各具优势与局限。
小结
本章揭示了定位滤波器在机器人自主性中的关键作用。
滤波器作为内置"GPS",持续校正运动模型预测与传感器数据,通过"预测-更新"循环防止误差累积,确保机器人始终掌握真实位置。
掌握状态认知、环境理解、运动控制和精确定位后,我们已准备好迎接机器人导航的终极挑战——路径规划!
下一章:路径规划算法
