I. Imagined Holly——The 2025 ICPC Asia Xi‘an Regional Contest(2025ICPC区域赛西安站)
I. Imagined Holly
题目链接:https://qoj.ac/contest/2558/problem/14689
题目大意:给定一个大小为 n×nn × nn×n 的非负整数矩阵 AAA。对于一棵具有 nnn 个顶点的树(顶点编号从 111 到 nnn),如果满足以下条件,则称该树为 holly tree:对于任意一对顶点 uuu 和 vvv(1≤u,v≤n1 ≤ u, v ≤ n1≤u,v≤n),矩阵元素 Au,vA_{u,v}Au,v 等于从 uuu 到 vvv 的简单路径上所有顶点编号的按位异或和。请你构造该树。
我们首先遍历矩阵,对于所有满足条件 a[u][v]=u∧va[u][v] = u \wedge va[u][v]=u∧v 的两点建立无向边,这样建出的图包含所有真边,同时会存在伪边(即存在两个点之间所有节点值的异或和等于 000),我们接下来的任务就是删去伪边。
我们称一个点 uuu 通过真边连接的点为真点,通过伪边连接的点为伪点,将真点和伪点都存入 nodes[u]nodes[u]nodes[u] 中。
对于点 uuu 来说,所有伪点 vvv 与 uuu 的路径 l1l_1l1 (除去点 vvv 和点 uuu)上的异或和等于 000,在路径 l1l_1l1 上最靠点 vvv 的一个点 www,不难知道 a[u][w]==ua[u][w] == ua[u][w]==u。我们将这样满足 a[u][w]=ua[u][w] = ua[u][w]=u 的点 www(除去 uuu 本身)记录到 same[u]same[u]same[u] 集合中。
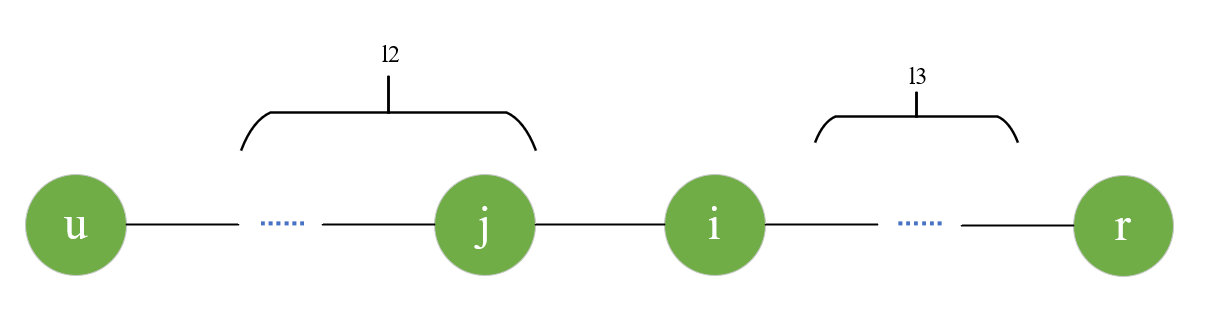
对于点 uuu,和 same[u]same[u]same[u] 集合中的一点 iii,以及点 uuu 和点 iii 的路径 l2l_2l2 (除去除去点 uuu 和点 iii),我们定义路径 l2l_2l2 上最靠点 iii 的点为 jjj,于是我们有以下结论:对于 nodes[i]nodes[i]nodes[i] 中的点 rrr,若满足点 iii 处于点 rrr 与 点 jjj 的路径上,则点 rrr 一定是点 uuu 的伪点。(证明1)
于是我们可以先枚举 same[u]same[u]same[u] 中的点 iii,然后枚举 nodes[i]nodes[i]nodes[i] 的点 kkk,在点 nodes[u]nodes[u]nodes[u] 中删去 kkk . 由于不满足上述条件的点 rrr 一定不存在于 nodes[u]nodes[u]nodes[u] 中,我们不需要进行特判。(证明2)
时间复杂度 O(能过)O(能过)O(能过)
证明1
满足点 iii 处于点 rrr 与 点 jjj 的路径上的情况如下图所示。如果点 rrr 是 nodes[i]nodes[i]nodes[i] 中的元素,则 l3l_3l3 要么不存在,要么异或和等于 000,由于 l2l_2l2 的异或和与 iii 异或等于 000(已知条件),所以 a[u][r]=u∧ra[u][r] = u \wedge ra[u][r]=u∧r,即点 rrr 是点 uuu 的伪点。
证明2
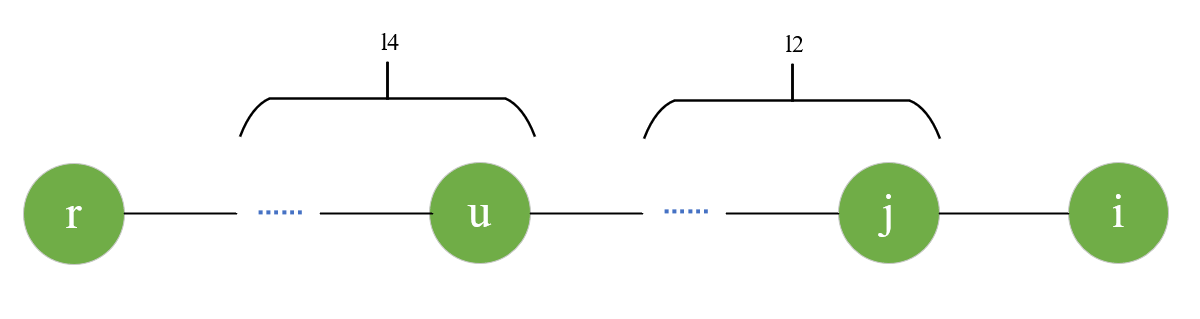
不满足证明 111 中条件的情况如下所示。l2l_2l2 与 l4l_4l4 路径上的异或和等于 000,l2l_2l2 上的异或和等于 iii,则 l4l_4l4 上的异或和等于 iii,若点 rrr 为点 uuu 的伪点,则 l4l_4l4 的异或和应等于 uuu,而 u≠iu \neq iu=i,因此点 rrr 不可能为点 uuu 的伪点。
点 rrr 处于点 uuu 右侧的情况和 r==jr == jr==j 的情况同理可以证明。因此枚举点 kkk 时不会存在误删。
证明3
下证明为什么这样删法可以将所有伪点删除。
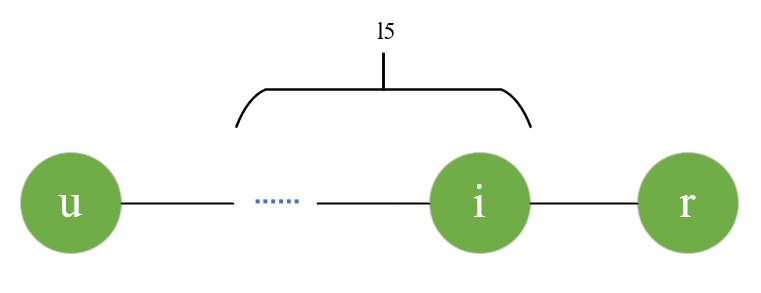
对于点 uuu 的一个伪点 rrr,一定存在非空且异或和为 000 的路径 l5l_5l5,并且 l5l_5l5 与点 rrr 相邻一点 iii 一定满足 a[u][i]==ua[u][i] == ua[u][i]==u,因此在 same[u]same[u]same[u] 中一定可以枚举到点 iii ,并可以将点 rrr 删去。
#include <bits/stdc++.h>
using namespace std;const int N = 2010;int n;
int a[N][N];
set<int> nodes[N], same[N];void solve()
{cin >> n;for (int i = 1; i <= n; i++)for (int j = i; j <= n; j++)cin >> a[i][j], a[j][i] = a[i][j];for (int i = 1; i <= n; i++)for (int j = i + 1; j <= n; j++)if (a[i][j] == (i ^ j))nodes[i].insert(j), nodes[j].insert(i);for (int i = 1; i <= n; i++)for (int j = 1; j <= n; j++)if (i != j && a[i][j] == i)same[i].insert(j);for (int u = 1; u <= n; u++)for (auto i : same[u])for (auto j : nodes[i])nodes[u].erase(j);for (int i = 1; i <= n; i++)for (int j : nodes[i])if (j > i) cout << i << ' ' << j << endl;
}int main()
{cin.tie(0);ios::sync_with_stdio(false);int Case = 1;while (Case --> 0) solve();return 0;
}
