深度学习（四）——logistic回归

4.1 二分分类

        logistic回归是一个用于二分分类的算法（binary classification），下图是一个二分分类问题的例子，假如你有一张图片作为输入，输出识别此图的标签，如果是猫猫，输出1，如果不是猫猫，输出0。使用y来表示输出结果的标签。来看看下面的图片，在计算机中是如何表示的呢？

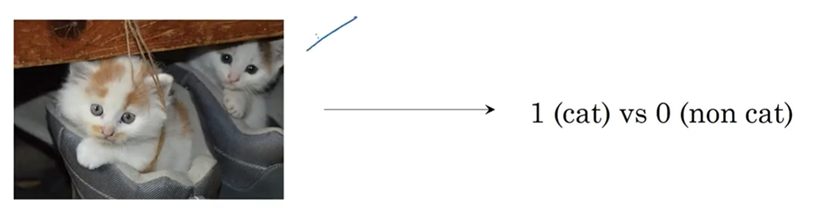
      计算机保存一张图片，需要三个独立矩阵，分别对应红、绿、蓝三个颜色的通道，如果输入图片是64×64像素，就有3个64×64的矩阵，为了更方便举例子，这里用三个5×4的小矩阵代替64×64的矩阵。把这些像素值都提取出来，放在一个特征向量x中(feature vector x)，步骤是先列出所有的红色像素，比如255、231等，接着是绿色像素255、134等，最后得到一个非常长的特征向量。如果图片是64×64像素，那么向量x的总长度就是64×64×3。对于这个例子，向量x的总长度是12288，用nx=12288来表示输入的特征向量x的维度，有时候为了简洁，也会用n来表述输入向量的维度。

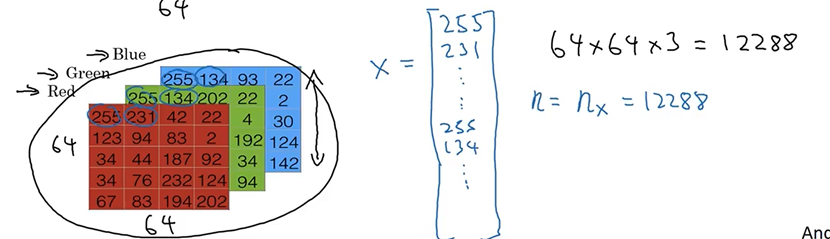
       在二分类的问题中，它以图片的特征向量x作为输入，预测输出结果标签为1还是0，也就是预测图中是否有猫猫。现在，看看后面课程中需要用到的一些符号。

        用一对来表示一个单独的样本，x是nx维的特征向量，。y是0或1。

        训练集由m个训练样本组成，用上标代表第 i个训练样本，表示样本一的输入和输出，表示样本二的输入和输出，表示样本m的输入和输出，这些在一起就表示整个训练集。用小写的字母m来表示训练样本的个数，有时候也写成。当说到测试集的时候，会用表示测试集的样本数。

        用更紧凑的符号表示训练集，定义一个矩阵，大写的X，它有由训练集中的x1、x2这些组成，放在矩阵的列中！为矩阵的第一列，为矩阵的第二列，最后得到矩阵X，这个矩阵有m列，m是训练集的样本数，矩阵的高度记作。所以X是一个的矩阵。在python中使用X.shape用来输出矩阵的维度，。

        输出y标签也放入列中，定义y是，y是一个的矩阵，在python中使用Y.shape用来输出矩阵的维度，。好的惯例符号能够将不同的训练样本的数据联系起来。

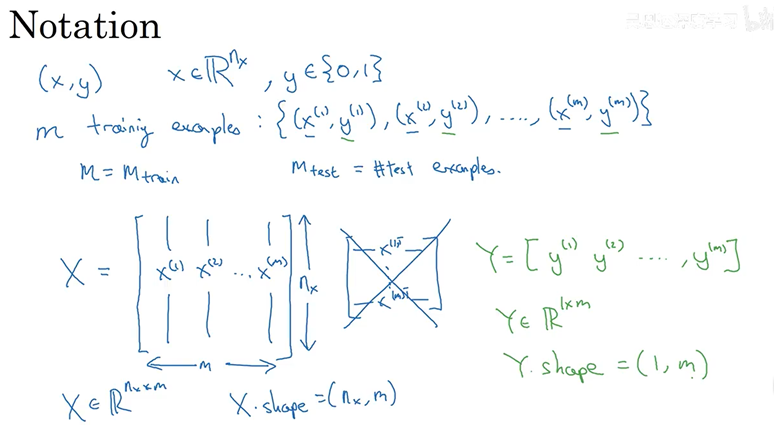
4.2 logistic回归

        这是一个学习算法，用于监督学习问题中，输出y标签是1或0时，二元分类问题。已知的输入特征向量x可能是一张图，你希望把识别出这是不是猫猫图。需要一个算法，可以给出一个预测值，，就是我们对y的预测，更正式来说，是一个概率，当输入特征满足条件的时候，y就是1，所以换句话说，x是图片，可以告诉你这张图片是猫猫图的概率。

        x是一个nx维的向量，已知logistic回归的参数是w，也是一个nx维向量，b是一个实数，所以已知输入x，和参数w、b，如何计算输出预测。可以按照下面那么试试，但是不一定靠谱：

       是输入x的线性回归，实际上如果做线性回归，就是这么算。但是这不是一个很好的二元分类算法。因为你希望是1的概率，所以应该介于0和1之间，但实际上很难实现，因为可能比1大很多，甚至是负数。这样的概率是没有意义的，所以在logistic回归中，我们的输出变成​​​​​​​等于sigmoid函数作用到这个量上，这就是sigmoid函数的图形，横轴是z，sigmoid(z)就是0到1的光滑函数。用z来表示。

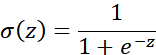
        当实现logistic回归时，要做的是学习参数w和b，​​​​​​​变成了对y=1的比较好的估计。

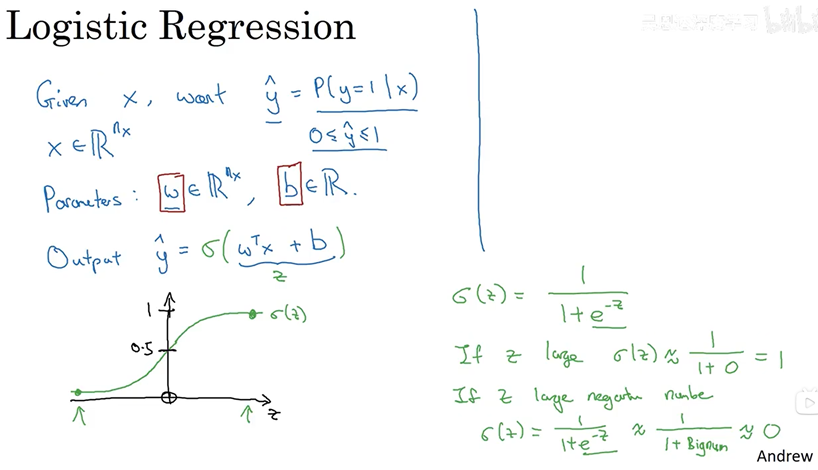
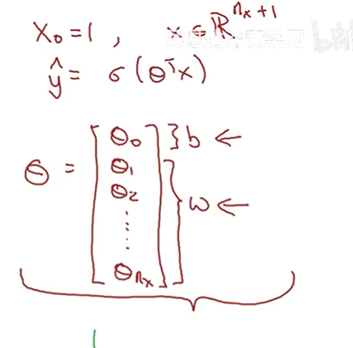
        在继续之前(moving on)，我们再讲一讲符号约定，当我们在神经网络编程时，通常会把w和b分开，在一些符号约定中，会定义一个额外的特征向量，叫x0，等于1，所以现在x就是维的向量，​​​​​​​定义为，定义如下，是一个实数，作用是b，到的作用和w一样。当实现你的神经网络的时候，把b和w看作独立参数更好。

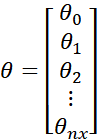
4.3 惯例符号的梳理（一）

        下面分析logistic回归中学习的惯例符号。

        x作为神经网络的输入，一般肯定不止有一个值，3个输入就是3个x，5个输入就是5个x，这里输入的值用nx表示！用下标表示第几个输入。这里先只考虑一个样本，以5个输入为例子，这5个x，分别表示为,用一个总的向量x表示，x是一个列向量！它的维度是：

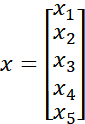
       此时，输出就是：

       让我们来看一看w是什么，w叫做权重，顾名思义就是不同输入x的权重，w也是一个列向量！它的维度是，都统一定义为列向量，同一个惯例比较好理解，做矩阵运算的时候，取w的转置，输出就是一个实数。是的权重，是的权重，后面同理！

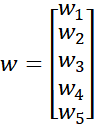
4.4 logistic回归的损失函数

        为了训练logistic回归模型中的参数w和b，需要定义一个成本函数，让我们来看一下，用来训练logistic回归模型的成本函数。为了让模型通过学习调整参数，需要给一个m个样本的训练集

       通过训练集找到参数w和b，来得到输出，对应训练集中的预测值，将它写成，希望它会接近于。为了让上面的方程更详细一些，需要说明上面定义的​​​​​​​是对于一个训练样本来说的，对于每个训练样本(traning example)，使用这些带有圆括号(round bracket)的上标(superscripts)，方便引用说明，还有区分样本！训练样本对于的预测值是，是使用训练样本通过sigmoid函数作用于得到的，可以进一步定义。

        现在让我们来看看损失函数(loss function)或者误差函数(error function)，可以用来衡量算法的运行情况，可以定义损失为：​​​​​​​和y差的平方或者差的平方的二分之一。但是在logistic回归中，大家通常不会这么做。因为当你学习这些参数的时候，你会发现后面的优化问题变成非凸(non-convex)的，最后会得到很多个局部最优解，梯度下降法，可能找不到全局最优值。

        所以在logistic回归中，我们定义一个不同的损失函数，它起到和误差平方相似的作用，但是会给我们一个凸的优化问题。损失函数定义如下：

        先直观看一看为什么这个损失函数可以起到作用，记得如果我们使用误差平方越小越好，对于这个logistic损失函数，我们也希望误差尽可能小，让我们来看看下面两个例子。

        当y=1的时候，如果希望尽可能的小，意味着尽可能的大，尽可能大，但是由于​​​​​​​来自sigmoid函数，最大就是接近1。

        当y=0的时候，如果希望尽可能的小，意味着尽可能的大，尽可能大，​​​​​​​尽可能的小，接近0。

       最后说一下，损失函数事在单个训练样本中定义的，它衡量了在单个训练样本上的表现，下面我要定义一个成本函数(cost function)，它衡量的是在全体训练样本上的表现。这个成本函数J，是所有训练样本的损失函数和。因此，在训练logistic回归模型时，我们要找到合适的w和b，让成本函数J尽可能的小。