优选算法(滑动窗口)
1. 长度最小的子数组
1.1 题目分析

由题可知:要求在一个全为正整数的数组中找一个连续的子数组,要求子数组中的每一个数相加和大于等于给定值(target)并且长度要最短。
1.2 解题思路
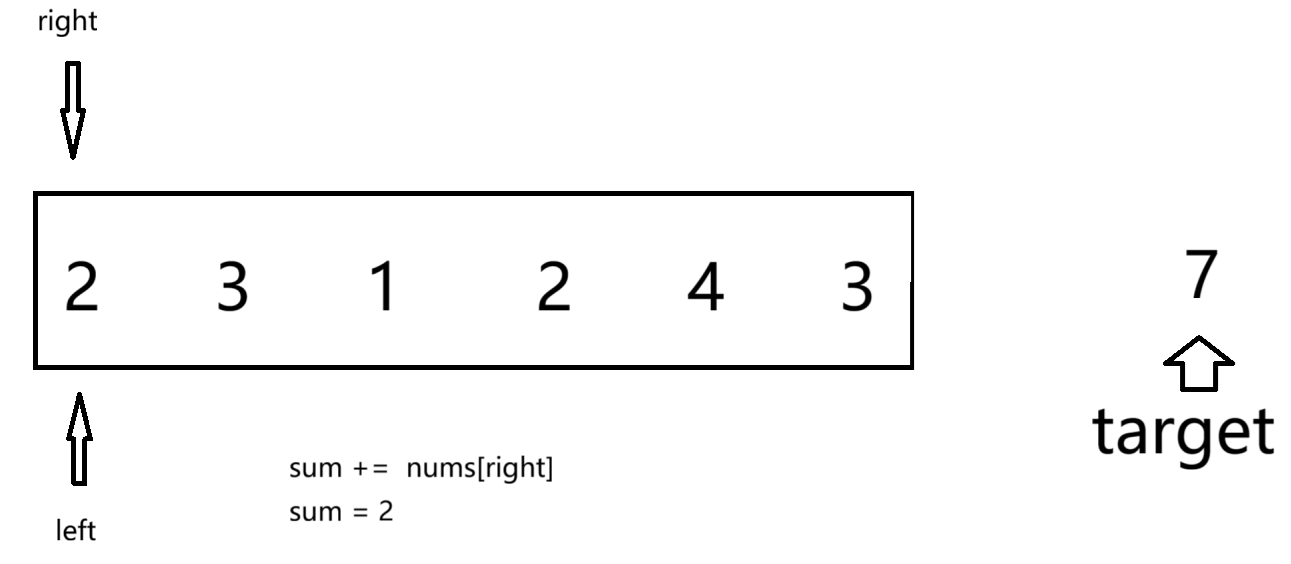
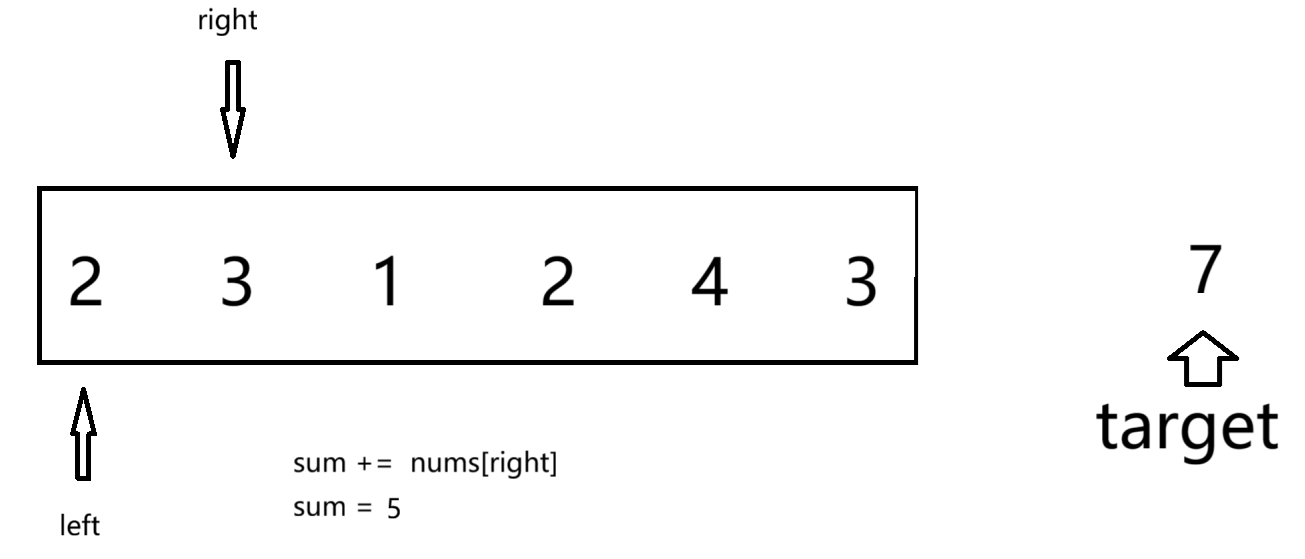
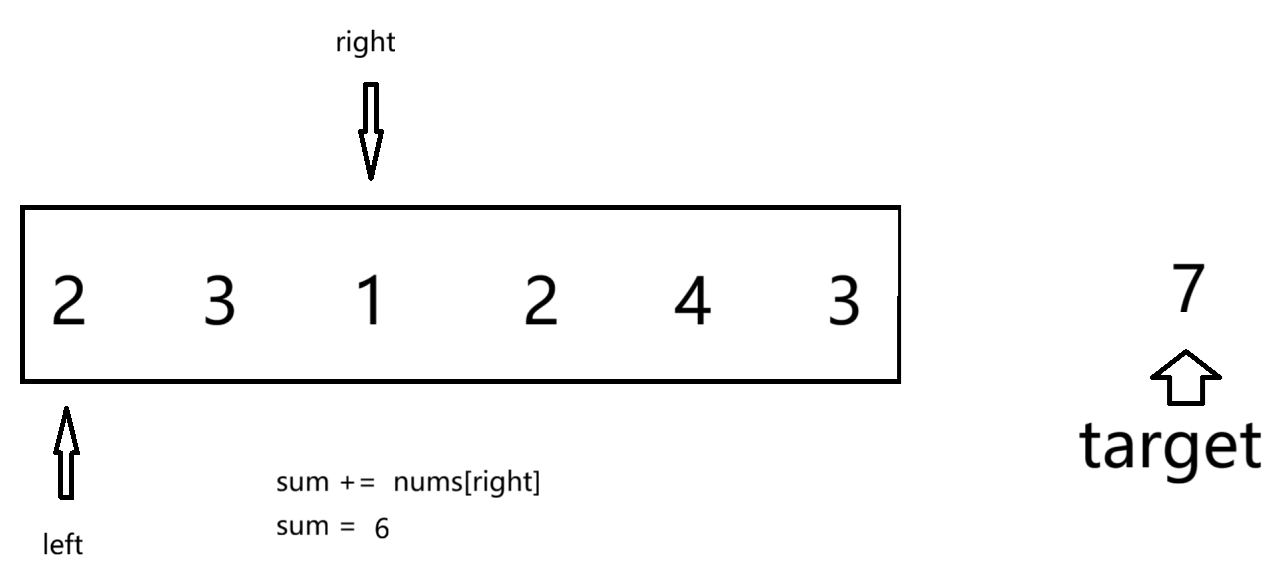
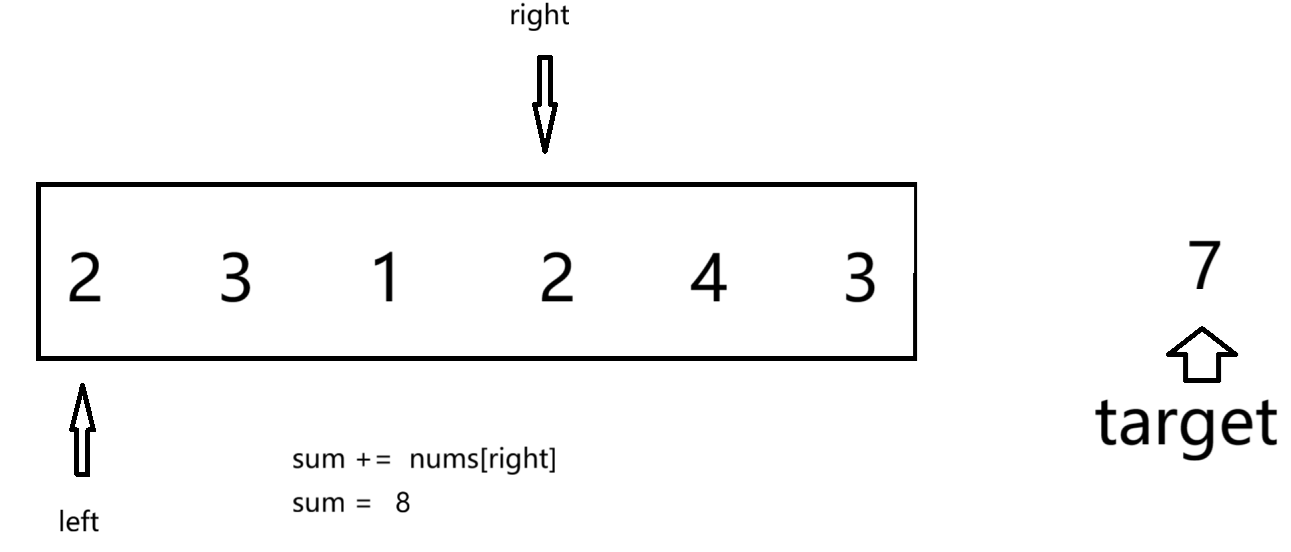
首先,定义两个标签left和right 都指向数组首元素,我们再定义一个sum计算right遍历元素的和,当sum大于target时,我们的到left和right围成子数组的长度为right-left+1。这时候我们不用再移动right,因为数组都为正整数 后面形成的子数组都会满足条件,但他们的长度不最小。
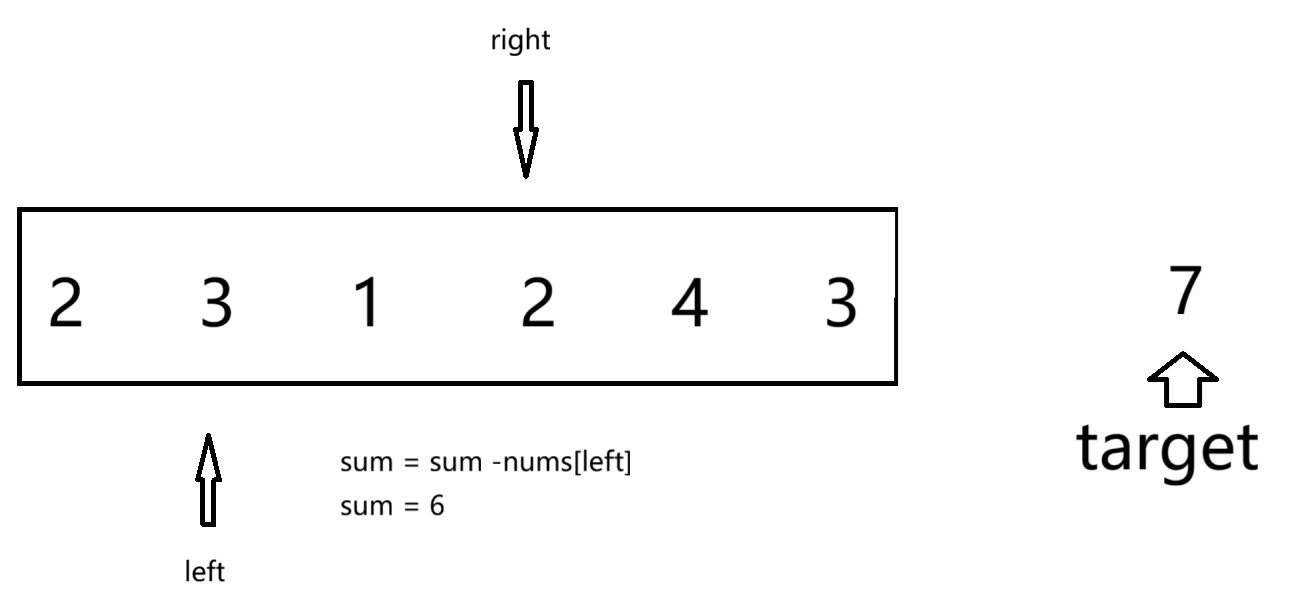
不难发现,组成子数组的可能性还没有完全判断,我们这时候移动left,不移动right,原因是sum的值可以直接算出来,为sum-nums[left]。然后重复进行上述操作,最后的到一个长度最小的子数组
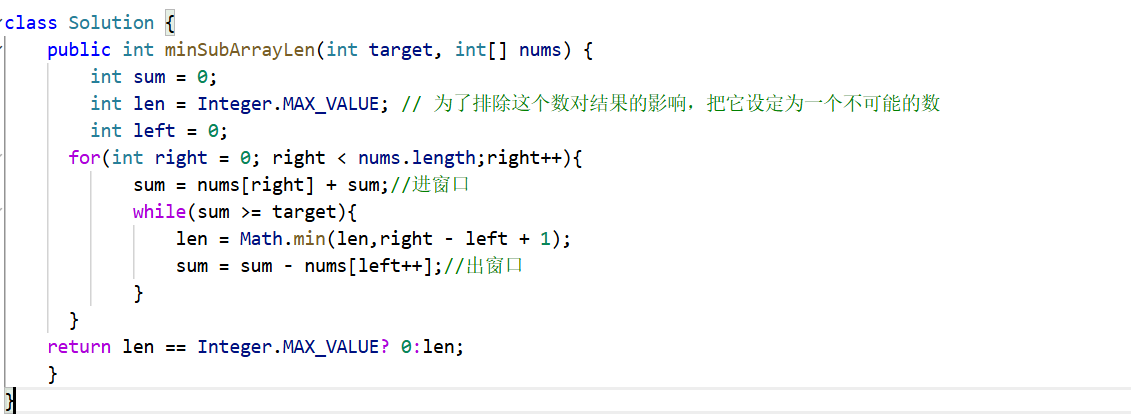
1.3 代码实现
1.4 复杂度
时间复杂度为:O(N)
空间复杂度为:O(1)
2.无重复字符的最大子串
2.1 题目分析


由题可知:我们要在字符串s中找一个连续的子串,要求子串长度最大并且不能有重复字符。
2.1 解题思路
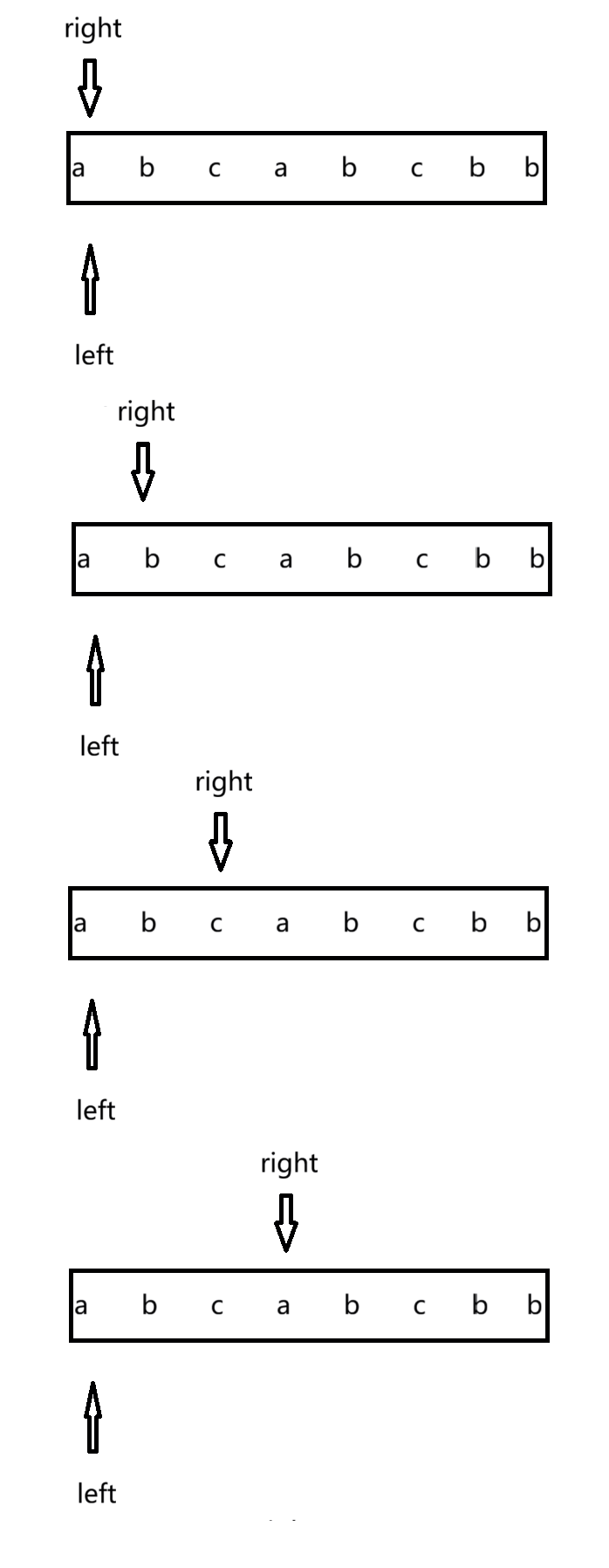
首先,我们先定义两个移动标签left 和 right,利用“动态窗口”的算法思想,left先不动先让right遍历数组元素, 可以通过hash表进行存储字符并进行查重。
 、
、
当出现重复字符时,我们可以更新得到一个子串长度(right - left + 1),这时候我们再进行遍历时移动right就没有意义了,我们需要移动left,改变原已服合要求的子串,寻找服合要求新的子串,而right可以不动因为我们迟早都会遍历到那个位置。
2.3 代码实现
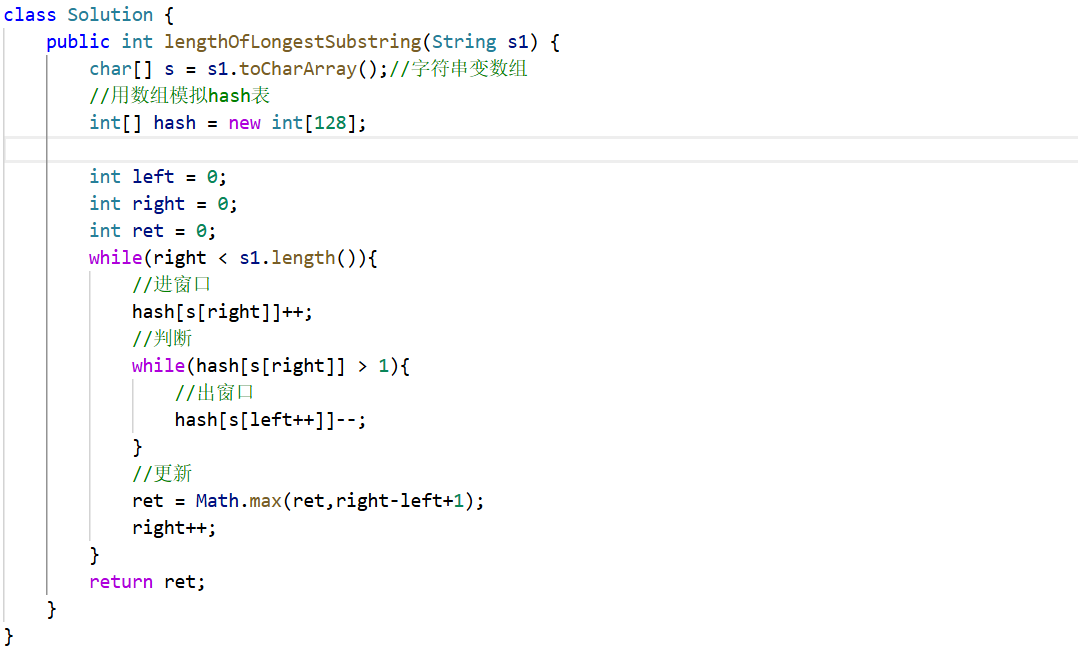
2.4 复杂度
时间复杂度:O(N^2)
空间复杂度:O(N)
3. 最大连续一的个数
3.1 题目分析

由题可知:在一个数组中只存在1和0,我们需要转换0为1(转换的次数小于等于k),使在数组中连续1的个数最长(在解题的过程中我们可以把要换的0直接看成1)
3.2 解题思路
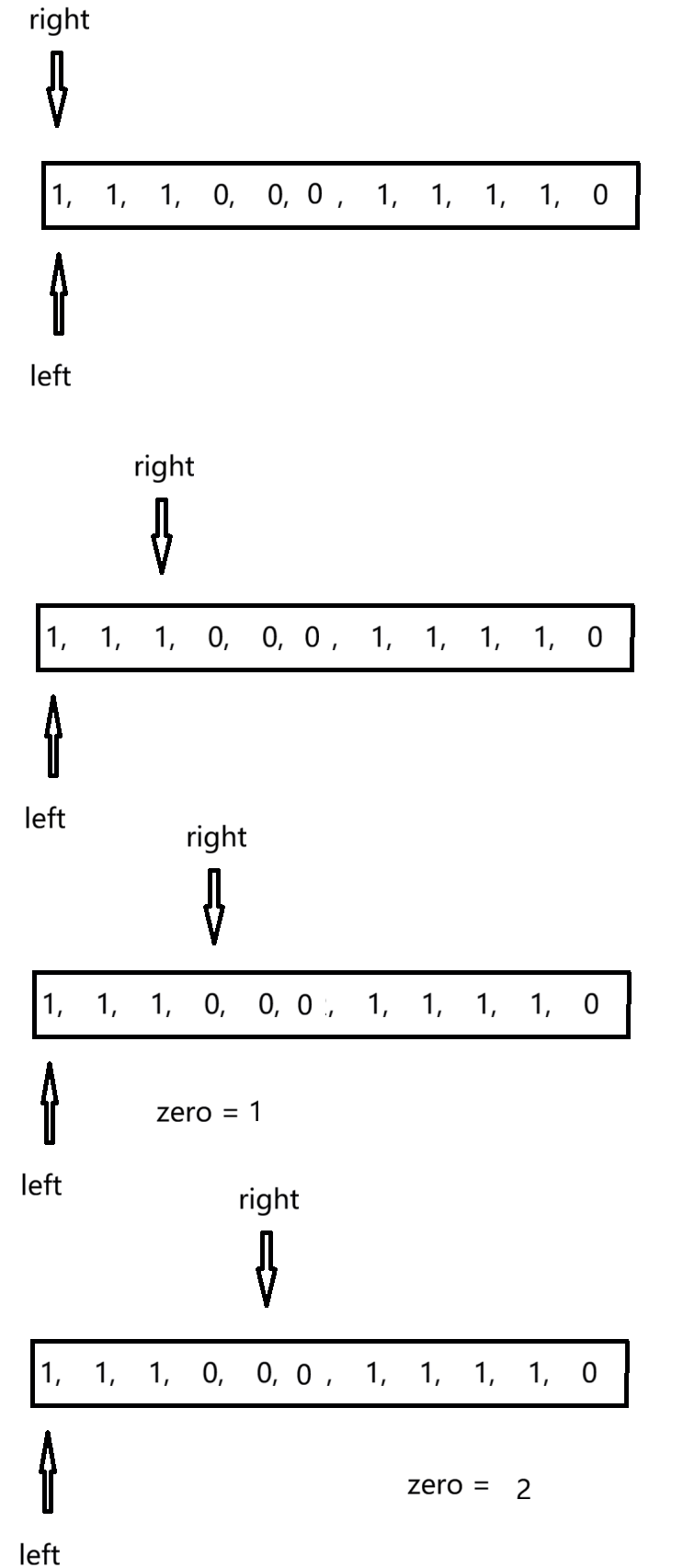
首先,我们可以定义两个下标标签left和right对数组进行遍历。如图所示,当right遍历到1时继续向后走,当遍历到0时我们通过一个计数器进行计数。
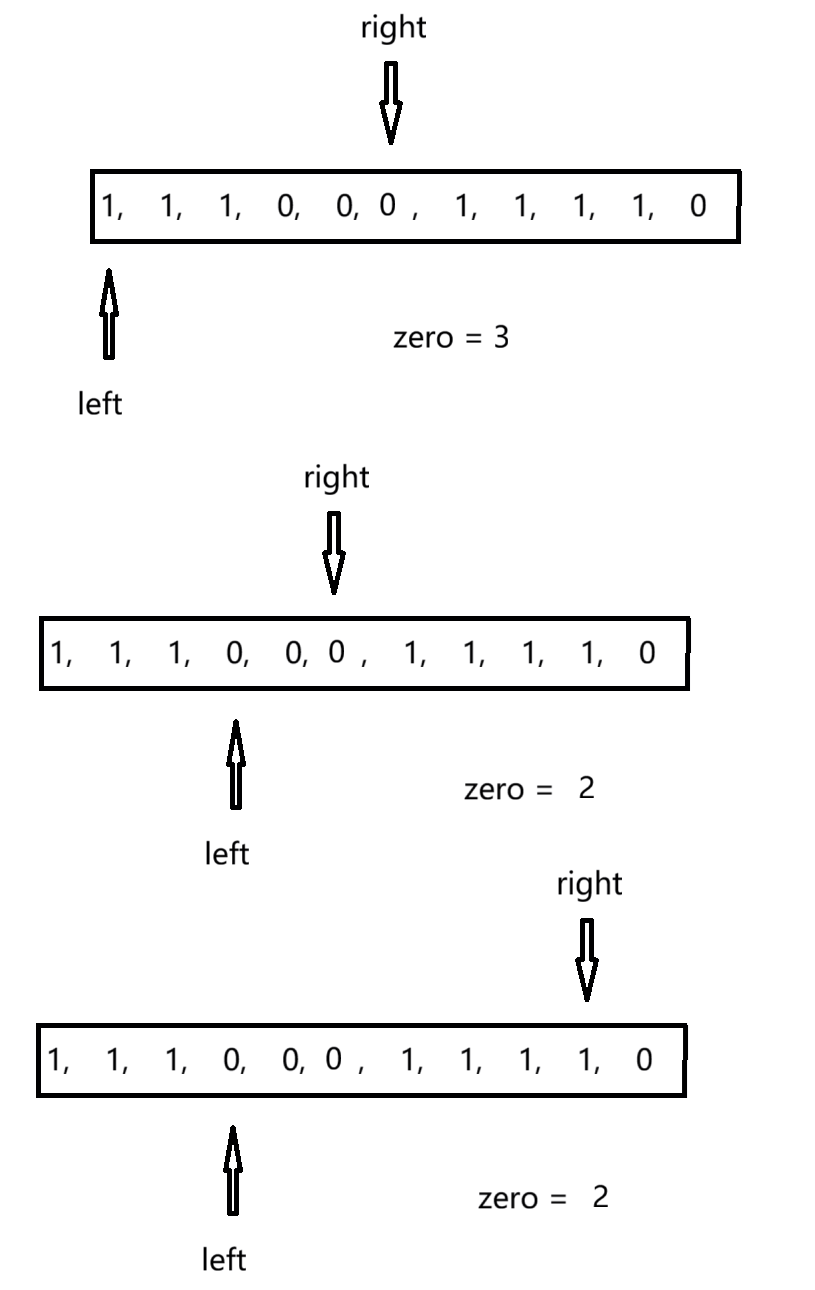
当 zero > k时我们将得到一个都为1的子数组,长度为:(right - left + 1)。此时left在该位置下的最长子数组已经找到,我们移动left进行重复操作,还是因为都会遍历到该位置所以right的位置可以不用动 。
3.3 代码实现
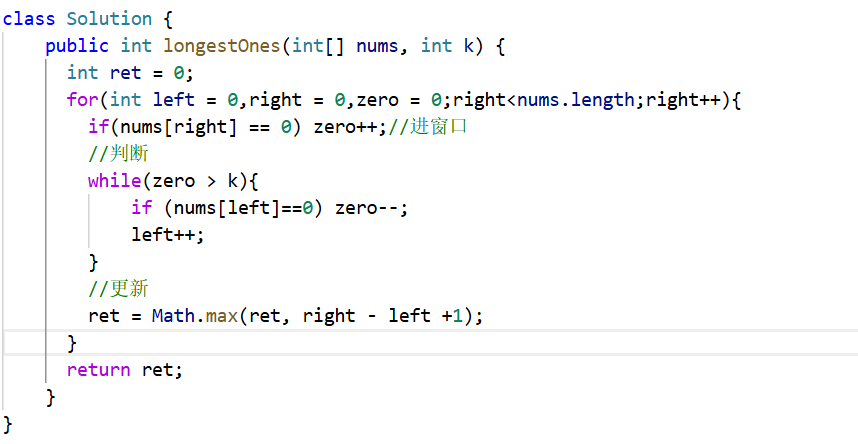
3.4 复杂度
时间复杂度:O(n)
空间复杂度:O(1)
4.将x减到0的最小操作数
4.1 题目分析


由题可知:我们要在数组的左右两边找元素,将x减去找到的数,使其最后为0,要求减数的个数要最小。我们发现正面解决问题很难,所以我们可以将问题转换为:在数组找到连续的子数组使其的值等于sum(数组元素总和)-x,要求找到的数组长度最大。
4.2 解题思路
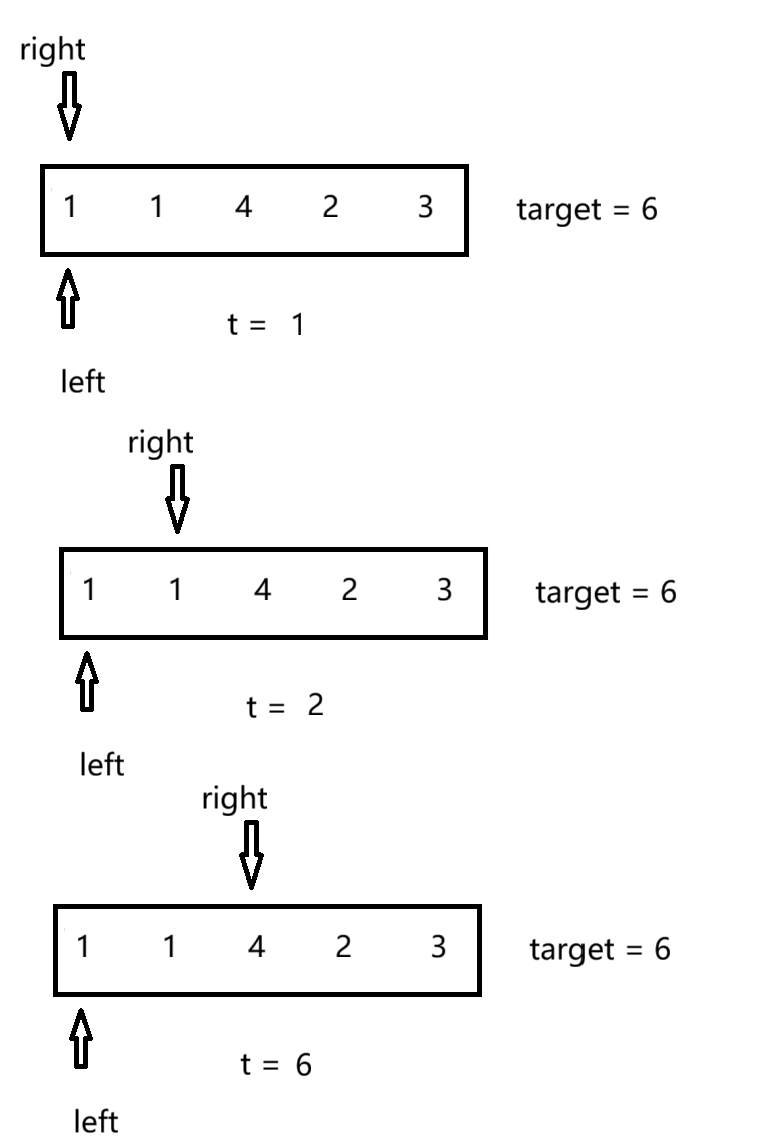
首先定义两个下标left和right一同指向数字首元素,计算出转换后需要达到的目标值target,通过移动right遍历数组,同时计算每个遍历数的和,当和等于目标值target时,更新计算当时数组长度。
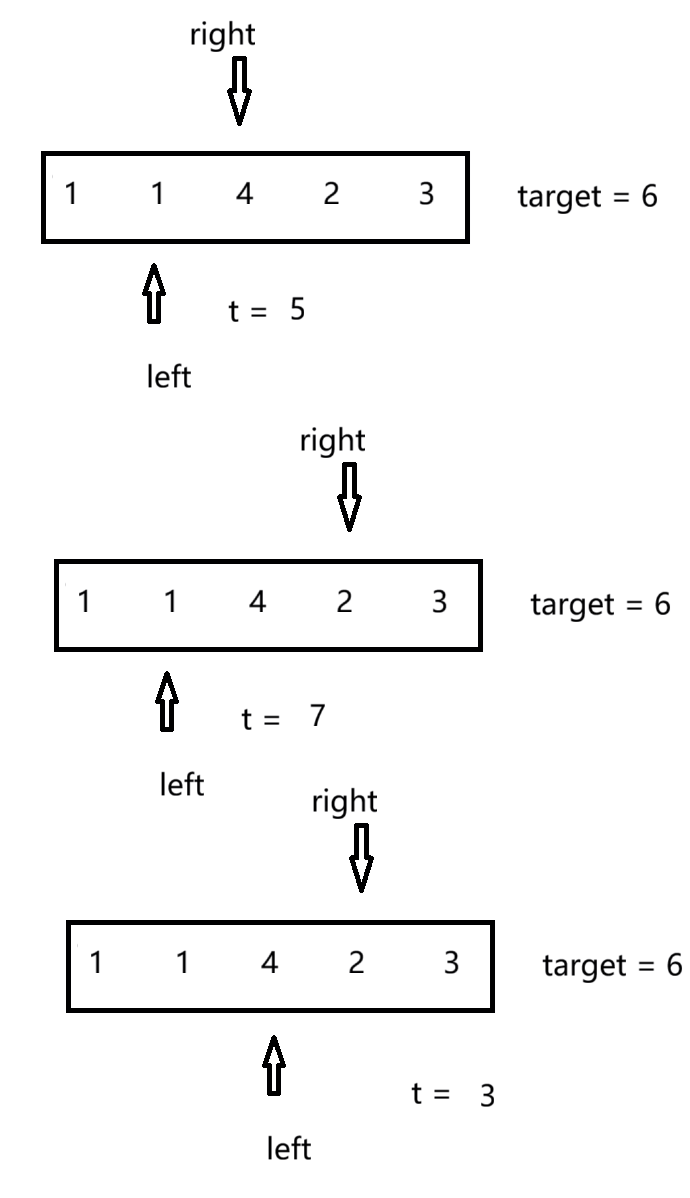
更新完后,我们移动left同时不动right(同理),当和大于目标值时,我们移动left然后重新判断。
注意:通过上述代码得到的结果要把数组长度减去该值才为目标值
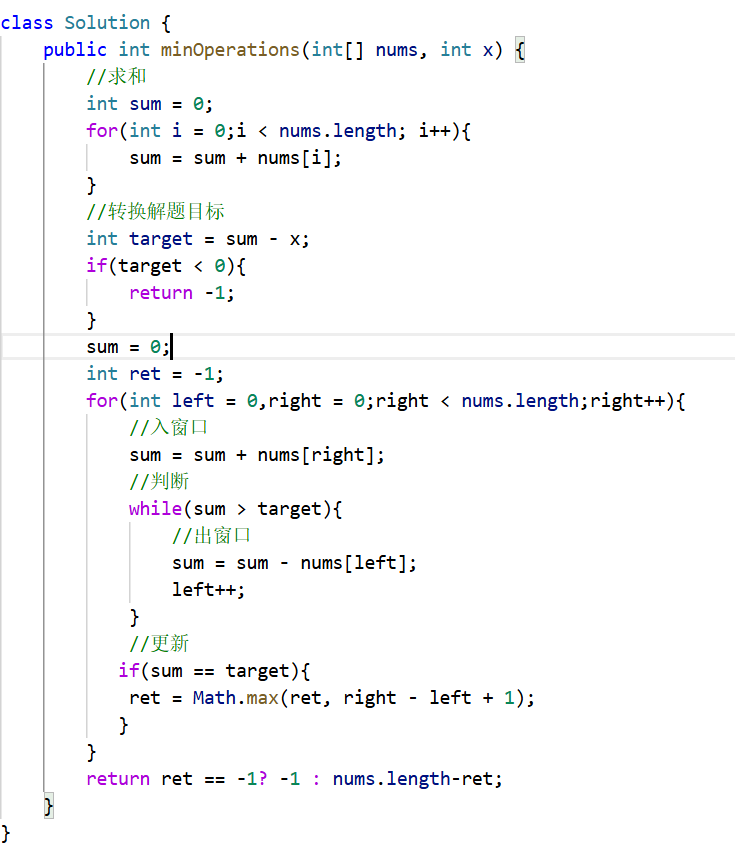
4.3 代码实现
4.4 复杂度
时间复杂度:O(n)
空间复杂度:O(1)
5. 水果成篮
5.1 题目分析

由题可知:需要在数组中找到子数组,该数组中只包含两种类型的水果,对同一种水果的个数没有要求。
5.2 解题思路
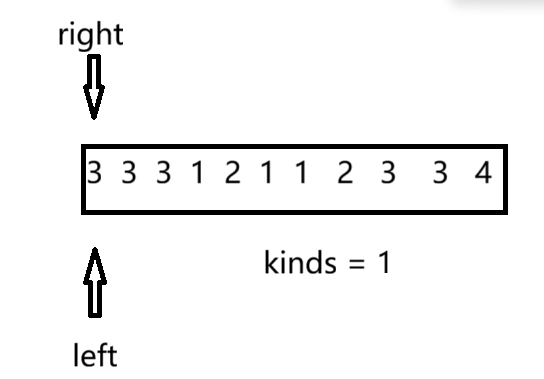
我们根据“滑动窗口”的算法思想,首先定义两个下标right和left,再定义一个kinds变量记录水果的种类。
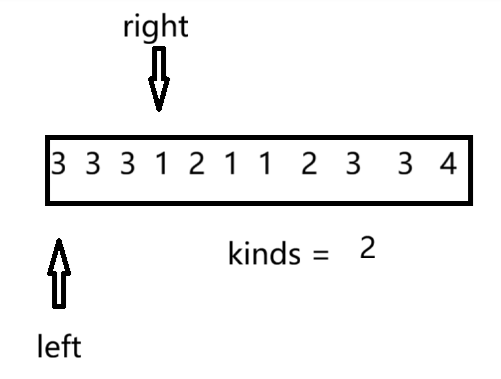
移动right遍历数组(入窗口)并通过hash表记录水果的种类和水果的数量。
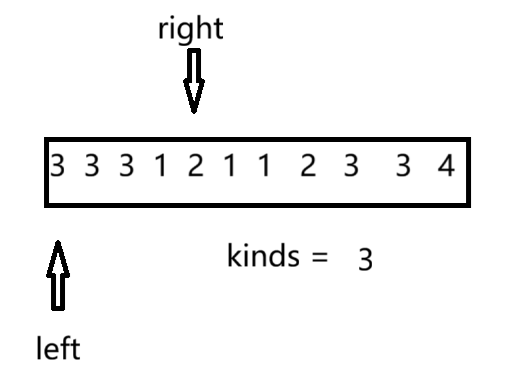
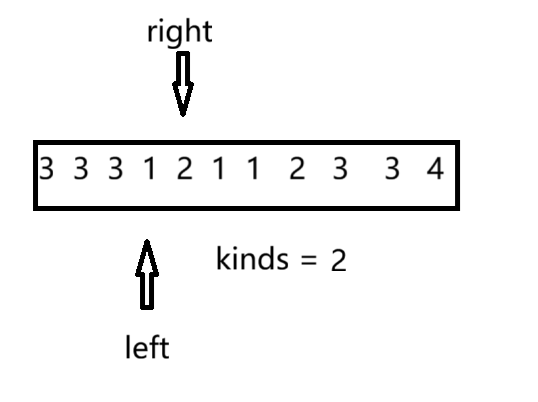
当水果种类大于指定值时,我们要移动left(出窗口)。在该过程中,分为两种情况:1. left该种类水果的数量大于0,此时将left++的同时将水果数量减一,2. left种类的水果数量等于0,此时我们要将left种类的水果除去,即left++并且kinds--。
大于指定值时,我们还需要更新该情况下子数组长度ret。
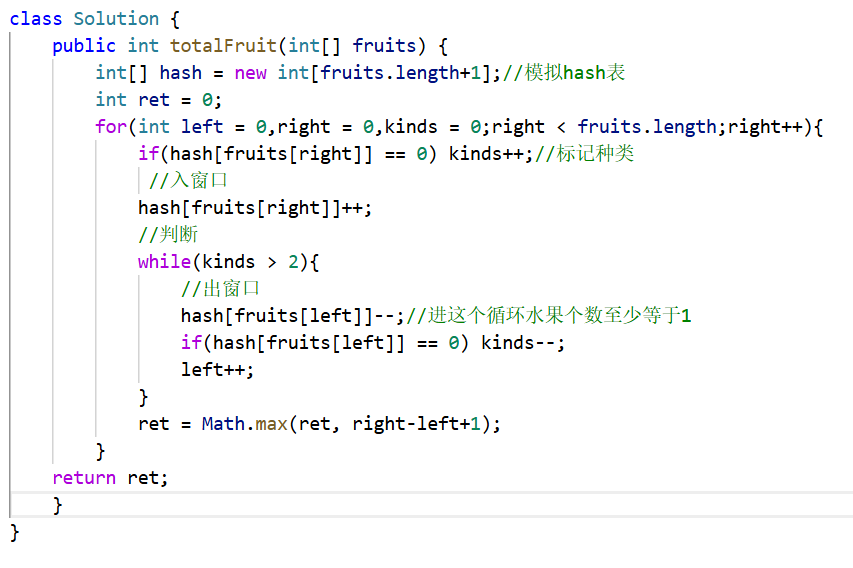
5.3 代码实现
5.4 复杂度
时间复杂度O(N)
空间复杂度O(N)
6. 找到字符串中所有字母异位词
6.1 题目分析


根据题目要求,在字符串s中找到所有为p变为词(长度相同,字母相对位置不同)的子串,结果返回所有子串开头位置的下标组成的列表。
6.2 解题思路
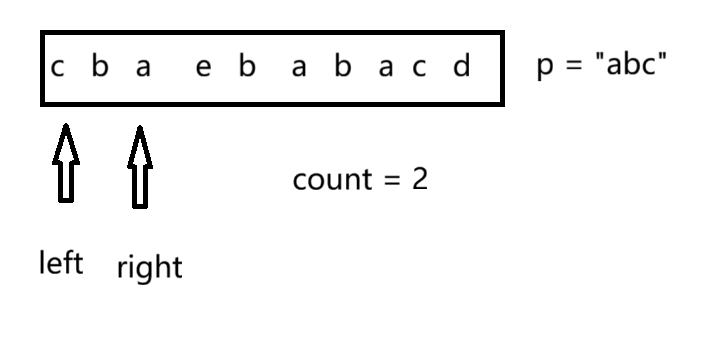
本题还是通过“滑动窗口”的算法思想进行解题,首先定义两个下标left和right,由于要找的子串长度为3,所以我们保持两下标的长度为3进行滑动,这里我们为了提高代码效率,我们定义一个记录当前子串有效字符个数的变量count。
我们还需先记录一下目标字符串有效数字的个数和类型,这里可以用到hash进行记录。分别在“入窗口”和“出窗口”时进行count个数的判断。
在“入窗口”时, 如果当前这个数在hash表上的个数小于在目标字符串上的个数时,count++,相等则继续遍。在“出窗口”时, 如果当前这个数在hash表上的个数小于在目标字符串上的个数时,count--。
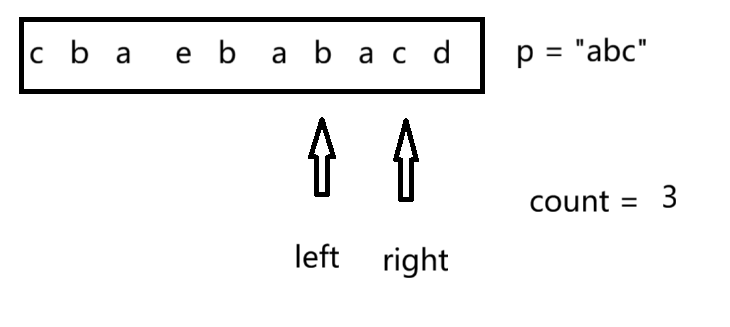
当count个数等于目标字符串个数时,即当前子串就是要找的目标子串,我们通过列表进行存储首元素下标left。
6.3 代码实现
6.4 复杂度
时间复杂度O(N+M)
空间复杂度O(1)
7. 串联所有单词的子串
7.1 题目解析

根据题目要求,我们将words数组中的字符串随意拼接,在s中找到与之相同的子串,返回所有子串首元素下标。
7.2 解题思路
我们只需将words中的字符串看成一个整体并将s中的字符串拆分成和words中字符串相同的子串,我们就会发现该题与上一题类似。
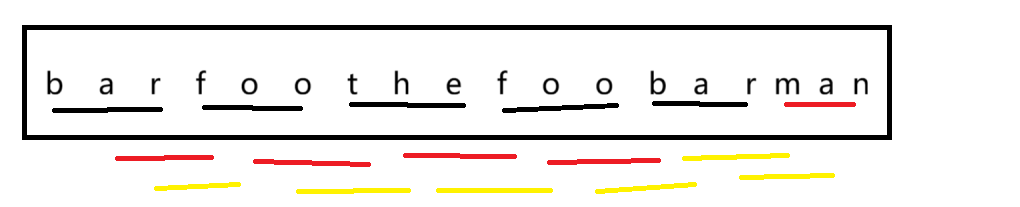
注意:
1. 我们对"滑动窗口"整体操作要重复进行,根据words数组每个元素的大小。原因是我们把s字符串的元素拆分了,导致有的结果无法遍历到。
2. 在执行“滑动窗口”的过程中right和left的更新不在是加1,而是加上一个words元素的大小
7.3 代码实现
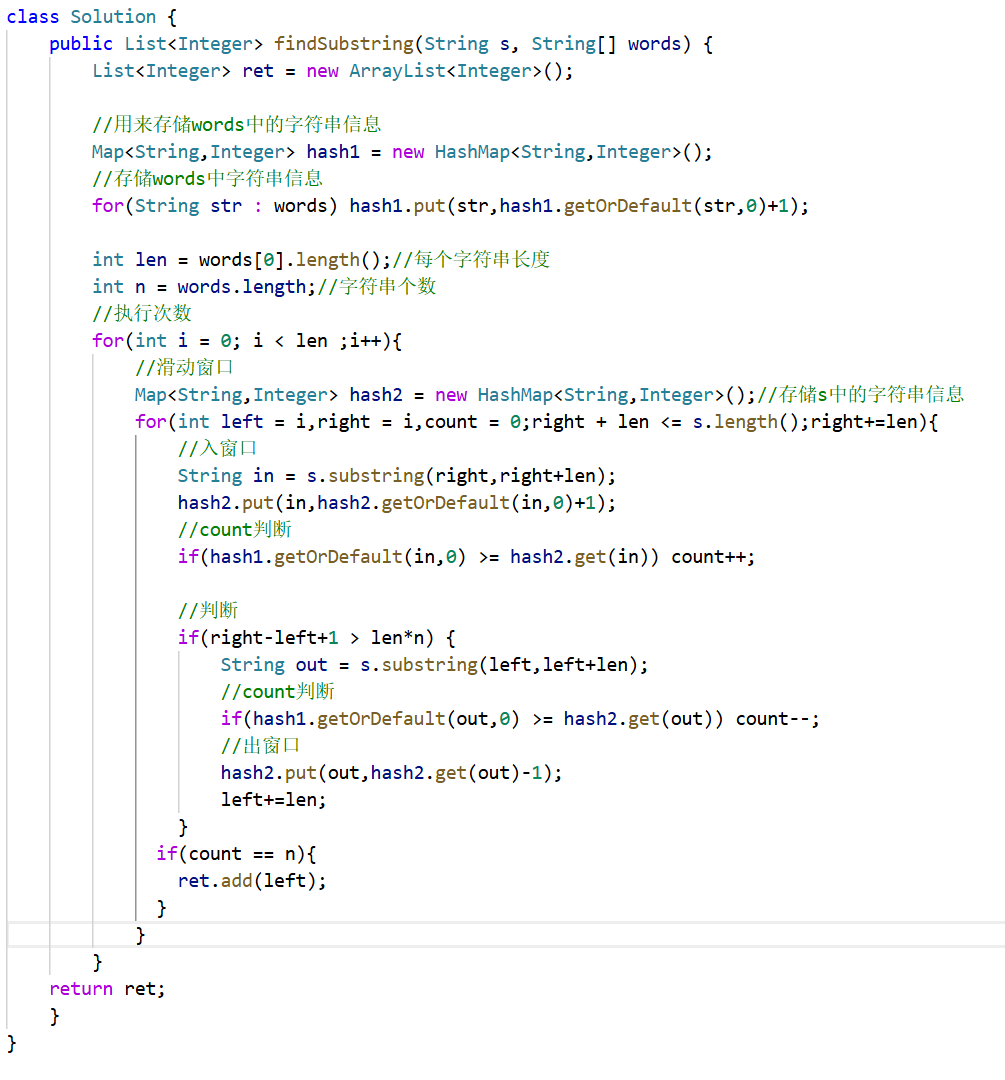
7.4 复杂度:
时间复杂度O(L)(L为s数组长度)
空间复度O(N)
8. 最小覆盖子串
8.1 题目解析


由题可得:要在字符串s中找到一个最小的子串,要求该子串包含字符串t中的所有元素,结果返回该子串。
8.2 解题思路
该题可以“滑动窗口”的算法思想来解决,定义left和right来遍历数组,通过定义两个hash表,hash1用来对目标数组元素信息的记录(例如:当记录元素a时分别记录它的类型和出现次数),hash2用来对被遍历数组元素信息的记录。
我们还可以通过一个变量count,记录hash2表中的有效元素,当hash2表中的元素种类并且出现次数和hash1表中的一样时,count++记录一次有效数字。反正如果任意一个不一样时count--。同这个变量我们可以在判断是否为需要子串时,避免对hash表从头到尾的遍历,从而提高代码效率。
8.3 代码实现
class Solution {public String minWindow(String s, String t) {char[] s1 = s.toCharArray();char[] t1 = t.toCharArray();//存目标元素信息int[] hash1 = new int[128];int kinds = 0; //目标字符种类for (char ch : t1) {if (hash1[ch] == 0)kinds++;hash1[ch]++;}int len = Integer.MAX_VALUE, begin = -1;int[] hash2 = new int[128];//滑动窗口for (int left = 0, right = 0, count = 0; right < s1.length; right++) {//入窗口char in = s1[right];hash2[in]++;//判断countif (hash1[in] == hash2[in])count++;//判断while (count == kinds) {//更新if (right - left + 1 < len) {len = right - left + 1;begin = left;}//出窗口char out = s1[left];//判断countif (hash1[out] == hash2[out])count--;hash2[out]--;left++;}}if (begin == -1)return "";elsereturn s.substring(begin, begin + len);}
}8.4 复杂度
时间复杂度:O(N)
空间复杂度:O(1)
