【高等数学笔记-极限(7)】函数连续

引例

例:函数在$x=1$处是连续的吗?
$$f(x)=\frac{x^2-1}{x-1}$$

讨论连续
要讨论函数在某一区间是否连续,即函数的图像应该是一条连续的线,即对于此区间上的任意点$x_0$;应该有距离$x_0$足够近的点,和此点的函数值一致,将这个距离记为$\Delta x$,即有:
$$\boxed{\underset{\Delta x\to 0}{\lim }\Delta y=\underset{\Delta x\to 0}{\lim }[f(x_0+\Delta x)-f(x_0)]=0}$$
或者描述为,足够靠近$x_0$处的函数值,趋近于$f(x_0)$,即:
$$\boxed{\underset{x\to x_0}{\lim }f(x)=f(x_0)}$$

讨论断开情况
或者描述为函数没有断开,什么是没有断开呢,考虑有以下三种断开的情况;

• 函数在这个区间的所有点都是要有定义的,定义断开了,函数指定是不连续了,例如以下函数在$x=0$处断开了
  $$f(x)=\frac{x^2}{x},f(x)=\sin \frac{1}{x}$$

• 函数在所有点的左右的值,准确说是所有点的左右极限应该是相等的,即某点的极限存在;否则也断开了;例如以下函数在$x=0$处发生了值的’跳跃’
  $$f(x)=\{\begin{array}{l}0,x<0\\ 1,x\ge 0\end{array}$$
  或者直接是趋于无穷的情况:
  $$f(x)=\frac{1}{x},f(x)=\frac{1}{|x|}$$

• 函数某点有定义,但是此点极限值不是函数值;例如
  $$f(x)=\{\begin{array}{l}x,x\ne 0\\ 1,x=0\end{array}$$

观察这几个函数的图像:
链接: 非连续函数

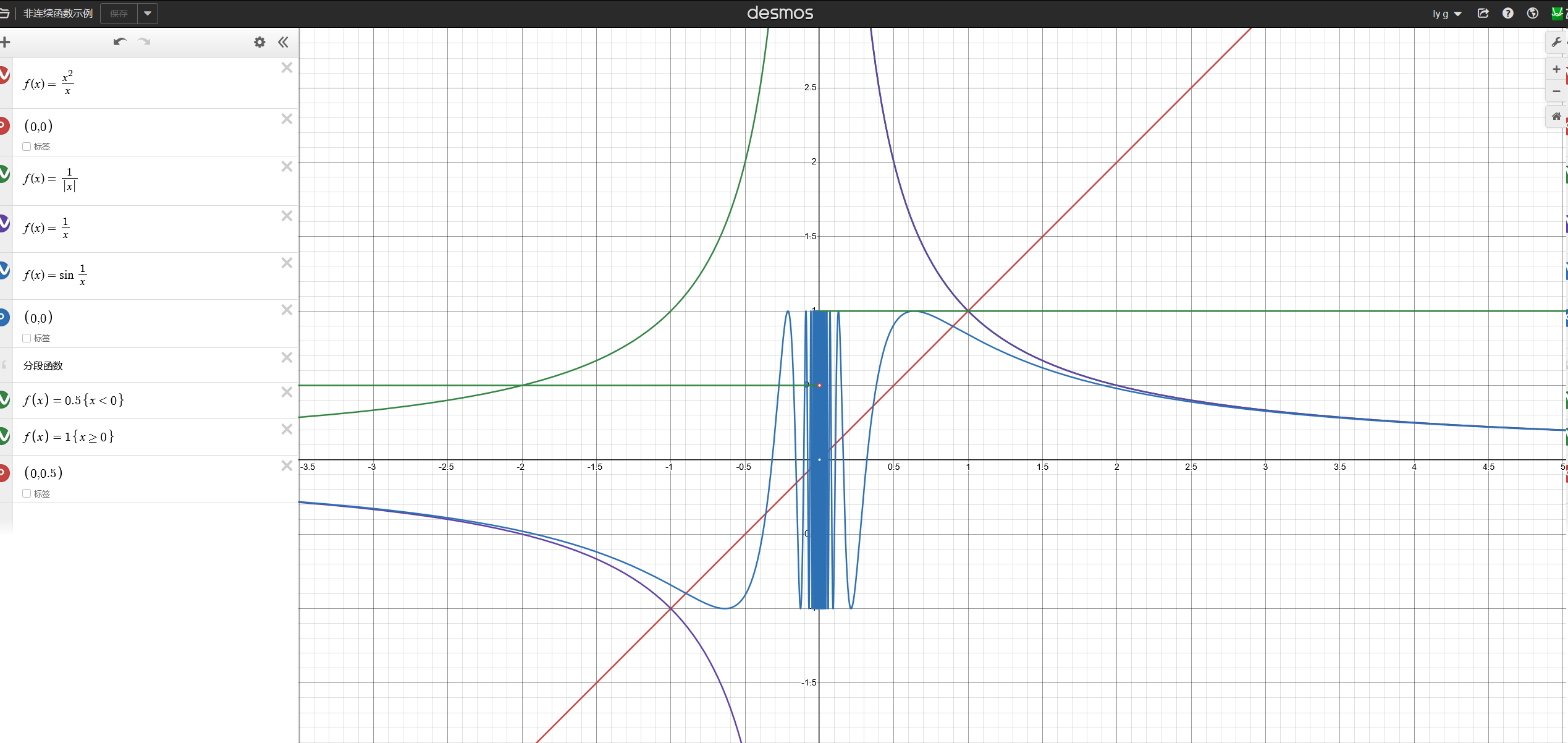
间断点

如果函数在某点$x_0$断开,则有以下可能:

1. 函数在$x=x_0$处极限不存在
   • 趋于无穷: 无穷间断点
   • 震荡发散: 震荡间断点
   • 左右极限都存在但不相等: 跳跃间断点
2. 函数在$x=x_0$处极限存在
   • 函数$x=x_0$处此点无定义或有定义,但不等于极限值: 可去间断点

可去间断点:实际就是有一个对总体可有可无的点,导致函数不连续的点;只要去掉他,函数就变成连续的了;
绘制到图像上实际就是一个连续函数的上面某点是一个空心圈,或者这个空心圈的上下有个点;对总体并无太大影响

• 第一类间断点:左右极限均存在的间断点:包含可去间断点和跳跃间断点
• 第二类间断点:左右极限至少有一个不存在的间断点:包含无穷间断点和震荡间断点

例题

• 例1. 讨论以下函数连续性和间断点;
  $$f(x)=\underset{n\to \infty }{\lim }\frac{1-x^{2n}}{1+x^{2n}}x$$
  解:
  $$\begin{gathered} f(x)=\underset{n\to \infty }{\lim }\frac{1-x^{2n}}{1+x^{2n}}x⟹f(x)=\{\begin{array}{ll}-x,& |x|>1\\ 0,& |x|=1\\ x,& 0<|x|<1\\ 0,& x=0\end{array} \\ x=-1,x=1时有第一类间断点,跳跃间断点 \end{gathered}$$
• 例2.设$$f(x)=\{\begin{array}{ll}x,& x\in \mathbb{Q}\\ 0,& x\in \mathbb{R}\backslash \mathbb{Q}\end{array}$$
  证明:
  (1) $f(x)$在$x=0$处连续;
  (2) $f(x)$在非零的$x$处都不连续;
  证:
  (1) 要证$f(x)$在$x=0$处连续;即证明$\underset{x\to 0}{\lim }f(x)=f(0)=0$
  即证明$\forall \epsilon >0,\exists \delta >0,使0<|x-0|<\delta 时,有|f(x)-0|<\epsilon$;
  取$\delta =\frac{\epsilon }{2}$(取$\epsilon$也可)
  当$x\in \mathbb{Q}$时:$|f(x)-0|<\frac{\epsilon }{2}<\epsilon$;
  当$x\in \mathbb{R}\backslash \mathbb{Q}$时,$|f(x)-0|=0<\epsilon$;
  得证;
  (2) 要证$f(x)$在非零的$x$处记为$x_0$都不连续;
  构建$f(x)$两个子数列,分别是趋于$x_0$的有理数数列和无理数数列,分别收敛于$x_0$和$0$,极限不一致,有数列和函数极限关系可得,函数$f(x)$极限不存在;故而函数不连续;

连续函数的复合函数

若内外函数均连续,则有
$$\begin{gathered} 计算:\underset{x\to x_0}{\lim }f(g(x))的极限 \\ 令u=g(x),\underset{x\to x_0}{\lim }g(x)=u_0 \\ 当函数f(u)在u_0连续,则有\underset{u\to u_0}{\lim }f(u)=f(u_0) \\ ⟹\underset{u\to u_0}{\lim }f(u)=f(\underset{x\to x_0}{\lim }g(x)) \\ g(x)也连续,适用复合函数极限定理有:\underset{u\to u_0}{\lim }f(u)=\underset{x\to x_0}{\lim }f(g(x)) \\ 则有:\boxed{\underset{x\to x_0}{\lim }f(g(x))=f(\underset{x\to x_0}{\lim }g(x))} \end{gathered}$$

即:若内外函数均连续,即可以将复合函数的极限挪到内函数上;
更一般的,外函数在$u_0$连续,内层函数有极限,也可适用

例题

• 例1
  $$\begin{array}{rl}& \underset{x\to 0}{\lim }\frac{\ln (1+x)}{x}\\ =& \underset{x\to 0}{\lim }\ln (1+x{)}^{\frac{1}{x}}\\ =& \ln \underset{x\to 0}{\lim }(1+x{)}^{\frac{1}{x}}\\ =& \ln e=1\end{array}$$

• 例2
  $$\begin{array}{rl}& \underset{x\to 0}{\lim }(1-2x{)}^{\frac{1}{\tan x}}\\ =& \underset{x\to 0}{\lim }{e}^{\ln (1-2x{)}^{\frac{1}{\tan x}}}\\ =& \underset{x\to 0}{\lim }{e}^{\frac{\ln (1-2x)}{\tan x}}\\ =& e^{{\lim }_{x\to 0}\frac{\ln (1-2x)}{\tan x}}\\ =& e^{{\lim }_{x\to 0}\frac{-2x}{x}}\\ =& e^{-2}\end{array}$$

根据例题2,实际找到了将两种不定式转换的方法
$$1^{\infty }\stackrel{x=e^{\ln x}⟹a^{\frac{1}{b}}=e^{\frac{\ln a}{b}}}{\Rightarrow }\frac{0}{0}$$

初等函数的连续

• 6类基本初等函数在其定义域中均为连续函数
  • 常数函数
  • 幂函数
  • 指数函数
  • 对数函数
  • 三角函数
  • 反三角函数
• 由基本初等函数经过有限次的四则运算或复合运算构造成的初等函数,在其定义域中均为连续函数
  • 有限次操作：不能通过无限次运算（如级数、极限）构造。
  • 仅允许四则运算与复合：不允许分段定义或非连续性操作。
• 初等函数的极限(如存在)等于函数值
• 初等函数的连续范围等于函数定义域
• 初等函数的间断点出现在没有定义点

例题

• 例1
  求$f(x)=x{\cos }^2\frac{1}{x}$的连续区间,间断点;
  解: 连续区间=定义域= { x ∣ x ≠ 0 } \{x|x\ne0\} {x∣x=0}
  间断点$x=0,{\lim }_{x\to 0}x{\cos }^2\frac{1}{x}=0$,为可去间断点;

• 例2:
  若函数$f(x),g(x)$是在$\mathbb{R}$上有定义,$f(x)\ne 0$且是连续函数;$g(x)$有间断点;问是以下函数否有间断点?

  • $g[f(x)]$
  • $[g(x){]}^2$
  • $f[g(x)]$
  • $\frac{g(x)}{f(x)}$

解:

1. $f(x)$的值域只要落在$g(x)$的连续区间上,那么复合函数$g[f(x)]$就是一个连续函数了;若 $f(x)$的值域跨域了间断点,则复合函数有间断点;所以不一定有间断点;
   不存在间断点的示例,复合函数的定义域变成了$D=[1,+\infty )$:
   $$f(x)=x^2+1,g(x)=\{\begin{array}{ll}1,& x\ge 1\\ -1,& x<1\end{array}$$
   存在间断点的示例:
   $$f(x)=x,g(x)=\{\begin{array}{ll}1,& x\ge 1\\ -1,& x<1\end{array}$$
2. 只要平方后间断点不存在了即可;
   不存在间断点的示例:
   $$g(x)=\{\begin{array}{ll}1,& x\ge 1\\ -1,& x<1\end{array}$$
   存在间断点的示例:
   $$g(x)=\{\begin{array}{ll}1,& x\ge 1\\ 2,& x<1\end{array}$$
3. $f(x)$本身连续的情况下,要出现间断点,只能是定义域不连续了,即$g(x)$的值域不连续;
   不存在间断点的示例:
   $$f(x)=x^2,g(x)=\{\begin{array}{ll}1,& x=0\\ x^3+2x^2-1,& x\ne 0\end{array}$$
   存在间断点的示例,区间$(0,1)$整个都断开了:
   $$f(x)=x,g(x)=\{\begin{array}{ll}x+1,& x\ge 0\\ x,& x<0\end{array}$$
4. 已知$g(x)$是$\mathbb{R}$上的不连续函数,若 $x_0$是$g(x)$的间断点,则有
   $$g(x_0)\ne \underset{x\to x_0}{\lim }g(x)$$
   假设若 $\frac{g(x)}{f(x)}$不存在间断点, 并且由于极限都存在,则对于任意点$x_1$都应有:
   $$\frac{g(x_1)}{f(x_1)}=\underset{x\to x_1}{\lim }\frac{g(x)}{f(x)}=\frac{{\lim }_{x\to x_1}g(x)}{{\lim }_{x\to x_1}f(x)}=\frac{{\lim }_{x\to x_1}g(x)}{f(x_1)}⟹g(x_1)=\underset{x\to x_1}{\lim }g(x)$$
   矛盾,故存在间断点;

闭区间上的连续函数的性质

• 有界性定理(最大值,最小值定理)
  闭区间上的连续函数,在此区间上有界即存在最大值和最小值;
  反例:

  • 若不限制闭区间,则区间端点是最大值最小值时,无法取到,只能无限趋近,故不存在最大值;
  • 若是非连续函数,则可能在区间中间断开,间断点趋向无穷,这样也不会有最大值

• 零点定理
  定义:设函数$f(x)$在区间$[a,b]$上连续,若$f(a)\cdot f(b)<0$,则在$(a,b)$上至少有一点$\xi$,使$f(\xi )=0$
  子区间应用定理:实际即使端点不是异号的,只要在此区间上存在两个异号的函数值,则至少有一个零点;
  反例:若非连续函数,则可两端分别趋于无穷,找不到零点

• 介值定理
  定义:设函数$f(x)$在区间$[a,b]$上连续,若$f(a)=A,f(b)=B$,对于$A,B$之间的任意一个值$C$,在$[a,b]$上至少有一点$\xi$,使$f(\xi )=C$.

• 值域范围
  设函数$f(x)$在区间$[a,b]$上连续,$M$是区间上的最大值,$m$是区间上的最小值,则值域为$[m,M]$,即$\forall x_0\in [a,b],m\le f(x_0)\le M$
  或者描述为,$\forall c\in [m,M],\exists \xi \in [a,b],f(\xi )=c$

例题

证明$x^5-3x=1$至少有一个根介于$1$和$2$之间;
证:设函数$f(x)=x^5-3x-1$,则$f(1)=-3,f(2)=25⟹f(1)\cdot f(2)<0$根据零点定理,至少存在一个$\xi$使得$f(\xi )=0$,得证

一致连续性,一致连续性定理

• 一致连续性实际是连续性的增强版;相对于连续性的要求,还要求函数不可以剧烈的变化;
  例如
  $$f(x)=\frac{1}{x}$$
  在$x>0$时是连续的,但不是一致连续的,在接近0处,函数急剧的变化,即因变量(函数值)的变化速度远远超过了自变量$x$的变化速度;
  定义表示只要自变量足够接近,函数值就可以足够接近;
  此函数在接近0处,即使自变量足够接近了,函数值依旧会相差非常大,故而不是连续一致的;

• 一致连续性定理
  如果函数$f(x)$在区间$[a,b]$上连续,那么函数在此区间上一致连续;
  实际端点可以取到值了,也就意味着端点连续了;