数据结构——二十七、十字链表与邻接多重链表(王道408)

前言

本文介绍了两种优化的图存储方案：十字链表存储有向图和邻接多重链表存储无向图。十字链表通过顶点节点和弧节点的双向链接，高效地记录入边和出边信息，空间复杂度为O(|V|+|E|)。邻接多重链表通过顶点和边节点的互连，避免数据冗余，每条边只存储一份数据，空间复杂度同样为O(|V|+|E|)。这两种方法分别针对有向图和无向图的特点进行了优化，相比邻接矩阵和邻接表在空间利用和操作效率上更具优势。

一.十字链表存储有向图(更优的有向图存储方案)

使用邻接矩阵存储有向图:空间复杂度高O(|V|²)
使用邻接表存储有向图:找顶点的入边不方便

1.示例图

1.示例图以及它的存储结构

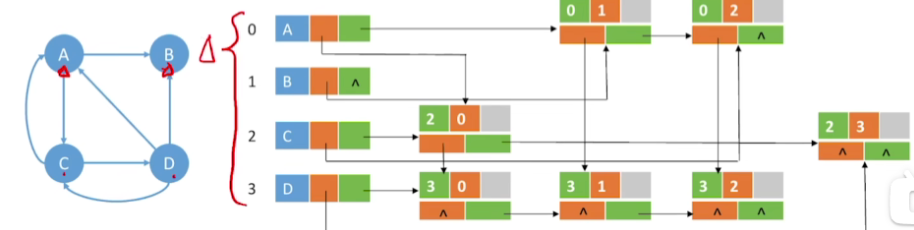
• ABCD的信息会分别存在数组的0123这几个位置,也就是说每一个节点是有一个编号的

• 那对于A节点来说,有一条弧是A指向B的,另一条弧是A指向C的

• 所以如果从A节点的绿色(firstout)往右边找会发现它指向的第一条弧的信息是从0号节点指向1号节点,也就是A指向B
  

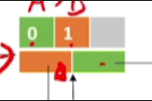
• 然后我们顺着这个节点绿色这个指针(tlink)继续往后找,找到下一个节点,这个节点表示的是从0号指向了2号,这两条弧是从A指向其他节点(弧尾相同)
  

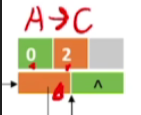
• 然后还有两条弧是从其他节点指向A(弧头相同)分别是D指向A和C指向A

• 那这两条弧的信息,我们要顺着A这个节点的橙色这个指针(firstin)往后面找

• 那这个橙色指针是指向了这一个弧的节点
  

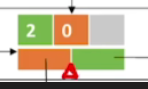
• 这个弧节点指明了,这条弧是从2号指向0号(C指向A)

• 那如果我们顺着这个弧结点的橙色这个指针继续往后找的话,那就可以找到下一条弧,这条弧是从3号指向0号,也就是从D指向A
  

• 那除了C和D指向A,没有其他节点指向A了,因此下面这个弧结点的橙色部分(hlink)指向为NULL

• 其他顶点结点和弧结点的构造方法也是一样的,不再赘述

2.弧结点的存储结构

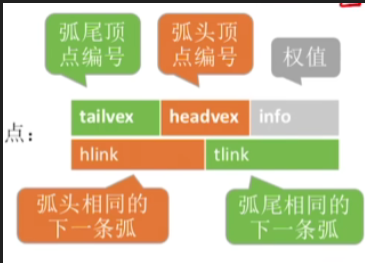
3.顶点节点的存储结构

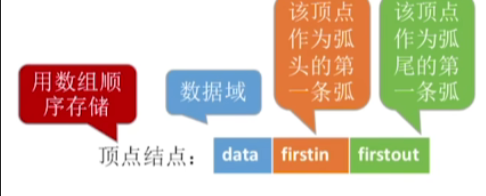
2.代码思路

• 用十字链表法来存储一个图的话,那么我们需要定义这样的两个结构体
• 其中一种结构体是表示顶点,另一种结构体是表示弧
• 如果我们通过绿色这一条指针线(firstout/tlink),一直往后找各个节点的话,那么我们就可以找到,从当前这个顶点往外发射的所有的这些弧,它们的总共的数量就是这个顶点的出度
• 而如果我们顺着橙色的这条指针(firstin/hlink),一直往后找的话,那我们就可以找到所有指向,当前这个顶点的弧,它们总共的数量就是这个顶点的入度

3.优势

• 想要找到和一个顶点相连的所有边,包括出边和入边都是很方便的

4.空间复杂度

• 空间复杂度：O(|V|+|E|)
• V表示顶点数,E表示边数

注意：十字链表只用于存储有向图

二.邻接多重链表存储无向图(更优的无向图存储方案)

使用邻接表存储无向图:每条边对应两份冗余信息，删除顶点、删除边等操作时间复杂度高
使用邻接矩阵存储无向图:空间复杂度高$O(|V^2|)$

1.示例图

1.示例图以及它的存储结构

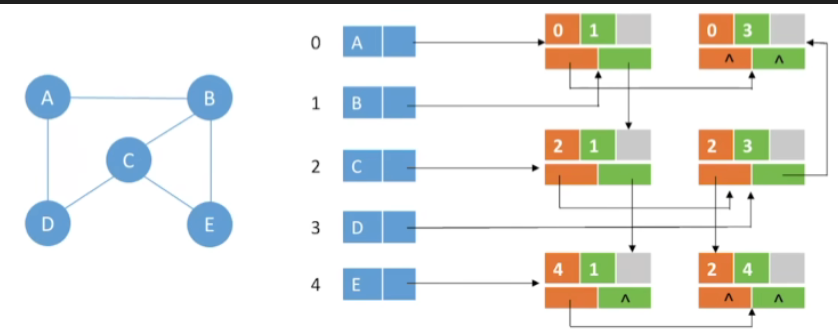
• 像这个无向图里边有五个顶点ABCDE,对应数组里面的01234

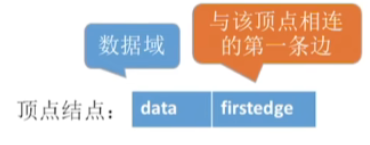
• 在顶点的信息当中,除了数据域之外,还需要有一个指针是指向和当前这个顶点相连的第一条边

• 比如对于A这个顶点,它和BD之间各有一条边,那我们顺着A节点的这个指针(firstedge)往后找,找到的这一条边,就是0号和1号相连的一条边,也就是A和B相连的一条边
  

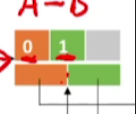
• 那在这个边节点里边,我们如果继续顺着iLink这个指针往后找的话,就可以找到和0号节点相连的下一条边,就是0号和3号相连的边
  

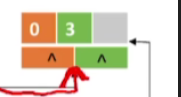
• 也就是A和D相连的这条边的信息,那除了这两条边之外,已经没有其他的边再和A相连了,所以这个节点的iLink指针是指向NULL,表示已经没有其他的边和a相连了

• 再来看B节点,对于B来说,有ACE这几个节点和它直接相连,那么我们通过B节点的这个指针往后找,找到第一条边的信息,这条边是A和B相连的一条边
  

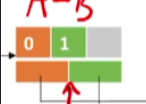
• 那由于这是一个无向图,所以B节点的编号1它到底是在左还是在右其实逻辑上来看是等价的

• 现在B节点的编号1是存在右边这个位置,所以如果我们要继续找到和B节点相连的下一条边的信息,那我们需要通过绿色这个指针(jLink)往后寻找

• 接下来的操作与前面类似,不做多赘述

1.边结点存储结构

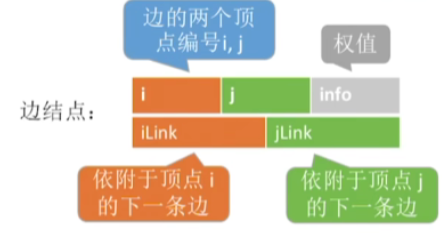
2.顶点结点的存储结构

2.优势

• 用邻接多重表的这种方式来存储无向图,想要找到和某一个顶点相连的边是很方便的
• 同时每一条边只会对应一个边节点只有一份数据,因此就不需要像邻接表那样同时维护两份冗余的数据,那这种特性可以保证我们在删除一个节点,或者删除一条边的时候操作起来会方便很多

3.空间复杂度

• 空间复杂度：O(|V|+|E|) (每条边只对应一份数据)

注意：邻接多重表只适用于存储无向图

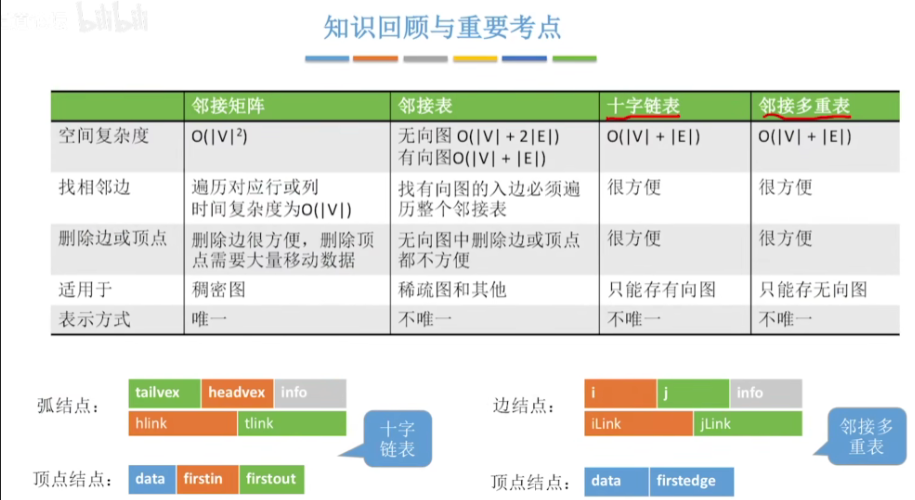
三.知识回顾与重要考点

结语

如果想查看更多章节,请点击:一、数据结构专栏导航页