强化学习-基本概念

一、基本的概念
1.1网格世界例子
图中有一个白色的智能体(Agent)在网格中移动,禁止区域不能进入,智能体的任务是从出发区域到达目标区域。

如果智能体知道网格世界的地图,那么可以规划一条到达目标单元格的路径。
但是如果事先不知道有关环境的任何信息,就需要智能体与环境进行交互,通过获取经验来找到一个好的策略。
1.2状态和动作
状态(state):描述了智能体与环境的相对状况。
状态对应了智能体所在单元格的位置。如下图对应着9个状态。所有的状态集合被称为状态空间(state space),表示为S = {s1,…,s9}。

动作(action)
如下图所示,智能体在每一个状态有五个可选的动作:向上、右、下、左移动和保持不动(对应a1,…,a5)。所有的动作集合被称为动作空间(action space),表示为A={a1,…,a5}。

注意,不同的动作可以有不同的动作空间,比如可以设置状态s1的动作空间为A= {a2,a3,a5},即直接把明显的不合理的动作从动作空间中删除。
1.3状态转移
当执行一个动作时,智能体可能从一个状态转移到另一个状态,这样的过程称为状态转移(state transition)。
比如,智能体处在s1,执行a2,那么智能体下个时刻移动到s2,这个过程可以表示为

两个重要问题
**问题一:**当智能体的下一步操作越过了网格世界的边界,他的下一时刻应该转移到什么状态?
因为网格世界是一个仿真世界,我们可以根据自己的喜好任意设置其状态转移过程(例如被弹回到原来的位置)。
如果是在现实世界,状态转移需要服从物理规律。
**问题二:**当智能体的下一步操作进入禁止区域,他的下一时刻应该转移到什么状态?
==》两种情况
1、虽然是禁止区域,但它仍然是“可进入”的,只不过进入的时候会受到惩罚。
2、禁止区域”不可进入“,智能体被弹回。
==》因为这是一个仿真环境,可以随意选择。本博客中选择第一种。之后会看到智能体可能会“冒险”穿过禁止区域,从而可以更快地到达目标区域。
每一个状态的每一个动作都会对应一个状态专业过程。这些过程可以使用一个表格来完成

在数学上,状态转移过程可以通过条件概率来描述。状态s1和动作a2的状态专业可以用如下条件概率描述:

==》当状态s1采取动作a2时,智能体转移到状态s2的概率为1,转移到其他任意状态的概率为0.
**扩展:**状态转移也可以是随机的,此时需要用条件概率分布来描述。
比如网格世界中有随机的阵风吹过,s1采取a2可能到达s5而不是s2。p(s5 | s1,a2) > 0,即下一个状态具有不确定性。
本博客只考虑确定性的状态转移过程。
1.4策略
**策略(policy)**会告诉智能体在每一个状态应该采取什么样的动作。
在直观上,策略可以通过箭头来描述。{如下(a)、(b)为一个确定性策略和对应的轨迹}

如果智能体执行某一个策略,那么他会从初始状态生成一条轨迹。

在数学上,策略可以通过条件概率来描述。通常使用π(a|s)来表示在状态s采取动作a的概率。这个概率对每一个状态和每一个动作都有定义。
在上图中的(a)(b)可以看到 状态s1对应的策略是:

该条件概率表名在状态s1采取动作a2的概率为1,而采取其他任意动作的概率为0。
上述例子中的策略是确定性的。策略也可能是随机性的。如下图的随机策略:在状态s1,智能体分别有0.5的概率采取向右和向左的动作。状态s1的策略是

除了使用条件概率,策略也可以用表格来描述。====》表格表示法
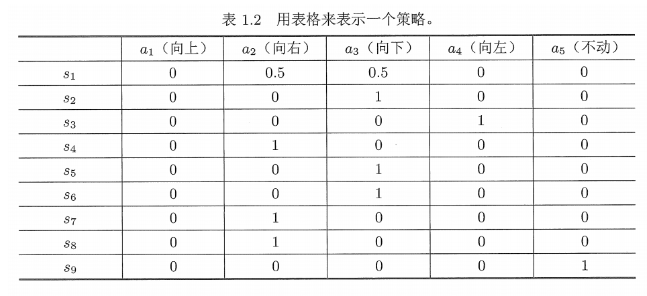
1.5奖励
**奖励(reward)**是强化学习中最独特的概念之一。
在一个状态执行一个动作后,智能体会获得奖励r。r是一个实数,它是状态s和动作r的函数,可以写成r(s,a)。其值可以是正数、负数或零。
正的奖励表示估计智能体采取相应的动作,负的奖励(也称为惩罚)反之。
在最初的网络世界例子中 可以设置越过四周边界或者进入禁止区域,设r=-1;到达目标区域,设r=+1;在其他情况下,r=0。
**注意:**当到达目标状态之后,也许会持续执行策略,进而持续获得奖励。
奖励实际上是人机交互的一个重要的手段:可以设置合适的奖励来引导智能体按照我们的预期来运动。
设计合适的奖励来实现我们的意图是强化学习的一个重要环节。
奖励的过程可以直观地表示为一个表格,如下图所示。
已知奖励表格,是否可以通过简单的选择对应最大奖励的动作来找到好的策略呢?
===》答案是否定的,这些奖励只是即时奖励,即在采取一个动作后可以立刻获得的奖励。具有最大即时奖励的动作不一定能带来最大的总奖励。
如果要寻找一个好的策略,那么必须考虑更长远的总奖励。

虽然直观,但是表格只能描述确定性的奖励过程。
为了描述更加一般化的奖励过程==》条件概率:p(r|s,a)表示在状态s采取动作a得到奖励r的概率。
对表格中的状态1:p(r = -1 | s1,a1)=1,p(r ≠ -1 | s1,a1)=0;这个奖励是确定性的==》表格和条件概率均可。
p(r = -1 | s1,a1) = 0.5,p(r = -2 | s1,a1) = 0.5 ==》各有0.5的概率获得-1或者-2的奖励 ==>奖励是随机的 =》只能条件概率。
该博客只考虑确定行的奖励过程
1.6轨迹、回报、回合
一条**轨迹(trajectory)**指的是一个“状态-动作-奖励”的链条。

如图(a),智能体从s1出发会得到如下轨迹:
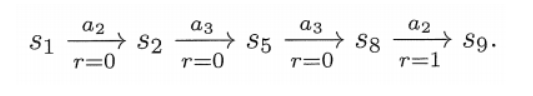
沿着一条轨迹,智能体会得到一系列的即时奖励,这些即时奖励之和被称为回报(return)。
上述轨迹对应的回报为 return = 0 + 0 + 0 + 1 = 1
回报由即时奖励和未来奖励组成。
即时奖励:在初试状态执行动作后立刻获得的奖励;
未来奖励:离开初始状态后获得的奖励之和。
在上述轨迹对应的即时奖励为0,未来奖励为1.
回报也称为总奖励或累计奖励。
回报可以用于评价一个策略的“好坏”。对于上图(a)(b)两个策略可以分别计算两条轨迹对应的回报,进而判断哪个策略更好。
(a) == > 回报为1;
(b) == >回报为0-1+0+1=0;
==》左边的策略相比右边的策略更能得到更大的回报 ==> 更好
轨迹是可以无限长的。到达目标之后保持不动,智能体会不断获得+1的奖励=》return = 0 + 0 + 0 +1 + 1 + 1 + …… = ∞ ==》引入折扣回报。
令γ∈(0,1)为折扣因子,折扣回报是所有折扣奖励的总和,即为不同时刻得到的奖励添加相应的折扣再求和:

由于γ∈(0,1),上式中的折扣回报的值不再是无穷,而是一个有限值:

引入折扣因子的作用:
1、它允许考虑无限长的轨迹,而不用担心回报会发散到无穷;
2、折扣因子可以用来调整对近期或者远期奖励的重视程度。
当执行一个策略进而与环境交互时,智能体从初始状态开始到终止状态停止的过程被称为一个回合(episode)或尝试(trial)。
如果一个任务做多有有限步,那么这样的任务称为回合制任务。
如果一个任务没有终止状态,则意味着智能体与环境的交互永不停止,这样的任务称为持续性任务。
在回合制任务中达到终止状态后,有如下两种方式将其转换为持续性任务。
第一,将终止状态视为一个特殊状态,从而使智能体永远停留在此状态,这样的状态称为吸收状态。即一旦达到这样的状态就会一直应留在该状态。
第二,将终止状态视为一个普通状态,将其与其他状态一视同仁,此时智能体可能会离开该状态并再次回来。由于每次到达s9都可以获得r=1的正奖励,可以预期的是智能体最终会学会永远停留在s9以获得更多的奖励。(需要使用折扣因子,以避免回报趋于无穷)。
博客更趋向于选择第二种情况。即让智能体学习到在到达这个状态之后能够保持原地不动。
1.7马尔可夫决策过程
马尔可夫决策过程是描述随机动态系统的一般框架。(强化学习需要依赖这个框架)
马尔可夫决策过程涉及以下关键要素:


马尔可夫过程与马尔可夫决策过程有什么区别和联系?
一旦在马尔可夫决策过程中的策略确定下来了,马尔可夫决策过程就退化成一个马尔可夫过程。
本博客主要考虑有限的马尔可夫决策过程,即状态和动作的数量都是有限的。

强化学习的过程涉及智能体与环境的交互,智能体之外的一切都被视为环境(environment)。
第一,智能体是一个感知者,例如具有眼睛能够感知并理解当前的状态;
第二,智能体是一个决策者,例如具有大脑能够做出决策,知道在什么状态应该采取什么行动;
第三,智能体是一个执行者,例如具有操作机构来执行策略所指示的动作,从而改变状态并得到奖励。
