当前位置：首页 > news >正文

算法笔记 06

news 2025/10/21 13:20:46

1 二叉树的实现

在 C 语言中，二叉树的实现方式主要围绕 “如何表示节点” 和 “如何组织节点间的关系” 展开。

二叉树的核心是 “每个节点最多有两个子节点（左子树和右子树）”，下面从最常见的实现方式开始，逐步拆解细节，并解释可能的疑惑点。

一、最常见的实现方式：链式存储（指针节点）

链式存储是二叉树最经典的实现方式，通过结构体 + 指针表示节点，用指针关联父节点与子节点。

1. 节点结构定义

首先定义二叉树的节点，每个节点包含 3 部分：

数据域：存储节点的值（如 int、char 等）；
左指针域：指向左子节点（若没有左子节点，指针为NULL）；
右指针域：指向右子节点（若没有右子节点，指针为NULL）。

代码示例：

// 定义二叉树节点
typedef struct TreeNode {int data;                  // 数据域（以int为例）struct TreeNode* left;     // 左子节点指针struct TreeNode* right;    // 右子节点指针
} TreeNode;

疑惑点 1：为什么要用struct TreeNode*而不是TreeNode*？因为在 C 语言中，typedef定义的别名（这里的TreeNode）在结构体内部还未生效（结构体定义还没结束），所以必须用struct TreeNode*来声明指针。C++ 中可以直接用别名，但 C 语言不行。

2. 创建节点（初始化）

要构建二叉树，首先需要创建单个节点，初始化其数据和指针：

// 创建新节点（分配内存并初始化）
TreeNode* createNode(int data) {TreeNode* newNode = (TreeNode*)malloc(sizeof(TreeNode));if (newNode == NULL) {    // 检查内存分配是否成功（关键！避免空指针）printf("内存分配失败\n");exit(1);}newNode->data = data;     // 赋值数据newNode->left = NULL;     // 初始时无左子树newNode->right = NULL;    // 初始时无右子树return newNode;
}

疑惑点 2：为什么要初始化为NULL？指针未初始化时会是随机值（野指针），后续判断 “是否有子节点” 时（如if (node->left != NULL)）会出错。初始化为NULL可以明确表示 “当前没有子节点”。

3. 构建二叉树（手动关联节点）

链式存储的二叉树需要手动通过指针关联节点，例如构建一个简单的二叉树：

int main() {// 创建根节点（值为1）TreeNode* root = createNode(1);// 给根节点添加左子节点（值为2）和右子节点（值为3）root->left = createNode(2);root->right = createNode(3);// 给左子节点添加左子节点（值为4）root->left->left = createNode(4);/* 此时树结构为：1/ \2   3/4*/return 0;
}

疑惑点 3：如何确定二叉树的 “根”？二叉树是 “有且仅有一个根节点（没有父节点）” 的结构，所有节点都通过指针最终追溯到根节点。构建时通常先创建根节点，再逐步添加子节点。

4. 链式存储的优缺点

优点：灵活，不需要预先知道树的大小，添加 / 删除节点时只需修改指针（时间复杂度 O (1)，前提是找到目标节点）。
缺点：指针需要额外内存（每个节点多 2 个指针的空间）；遍历节点时只能通过指针逐个访问（不能随机访问，如直接访问第 k 个节点）；可能出现内存碎片（频繁 malloc/free 时）。

二、其他实现方式

除了链式存储，还有一些特殊场景下的实现方式，核心是用 “非指针” 的方式表示节点间的关系。

1. 数组存储（适用于完全二叉树）

完全二叉树的结构特殊：除最后一层外，每层节点都满，且最后一层节点从左到右连续（如堆就是完全二叉树）。这种结构可以用数组存储，通过下标计算节点间的关系，无需指针。

节点下标规则（假设根节点下标为 0）：

对于下标为i的节点：
- 左子节点下标 = 2*i + 1
- 右子节点下标 = 2*i + 2
- 父节点下标 = (i-1) / 2（整数除法）

代码示例：

#define MAX_SIZE 100  // 预先定义数组最大容量
int tree[MAX_SIZE];    // 存储完全二叉树的数组
int size = 0;          // 当前树的节点数量// 添加节点（按层次顺序，保证完全二叉树特性）
void addNode(int data) {if (size >= MAX_SIZE) {printf("树已满\n");return;}tree[size] = data;  // 新节点放在最后一个位置size++;
}// 获取左子节点的值（返回-1表示不存在）
int getLeftChild(int i) {int left = 2*i + 1;return (left < size) ? tree[left] : -1;
}

疑惑点 4：为什么只适用于完全二叉树？如果是普通二叉树（存在空节点且不连续），用数组存储会浪费大量空间。例如，一个左斜树（所有节点只有左子树），数组中会有很多位置空着（右子节点下标对应的位置）。

优点：节省指针空间，访问子节点 / 父节点时通过公式计算（O (1) 时间），适合存储完全二叉树（如堆排序中的堆）。缺点：不适合普通二叉树（空间浪费），大小固定（需预先定义 MAX_SIZE），插入 / 删除非末尾节点时需要移动大量元素（时间复杂度 O (n)）。

2. 带父指针的链式存储（便于回溯）

普通链式存储只有左、右子指针，若需要从子节点回溯到父节点（如某些遍历场景），可以给节点增加一个 “父指针” 域。

结构定义：

typedef struct TreeNode {int data;struct TreeNode* left;   // 左子struct TreeNode* right;  // 右子struct TreeNode* parent; // 父节点指针
} TreeNode;

创建节点时需要额外初始化父指针，添加子节点时同步更新父指针：

// 给parent节点添加左子节点
void addLeftChild(TreeNode* parent, int data) {TreeNode* child = createNode(data);parent->left = child;child->parent = parent;  // 子节点的父指针指向parent
}

适用场景：需要频繁从子节点向上遍历（如查找某个节点的祖先），避免重新从根节点遍历。缺点：每个节点多一个指针的内存开销。

3. 线索二叉树（解决空指针浪费问题）

普通链式存储中，叶子节点的左、右指针都是NULL（空指针），这些空指针可以被 “利用” 起来，存储遍历顺序的前驱 / 后继节点地址（称为 “线索”），这样遍历二叉树时无需递归或栈，直接通过线索访问。

结构定义（增加标志位区分 “指针是子节点还是线索”）：

typedef struct ThreadNode {int data;struct ThreadNode* left;struct ThreadNode* right;int ltag;  // 左标志：0=左指针指向子节点，1=左指针是前驱线索int rtag;  // 右标志：0=右指针指向子节点，1=右指针是后继线索
} ThreadNode;

原理：

若节点无左子节点（left=NULL），则ltag=1，left指向遍历顺序中的前驱节点；
若节点无右子节点（right=NULL），则rtag=1，right指向遍历顺序中的后继节点。

优点：充分利用空指针，遍历（如中序遍历）时无需栈或递归，时间效率高。缺点：结构复杂，插入 / 删除节点时需要同步维护线索（容易出错），适合静态树（构建后很少修改）。

三、总结：如何选择实现方式？

实现方式	核心特点	适用场景
普通链式存储	左 / 右指针，灵活	大多数场景（普通二叉树、二叉搜索树等）
数组存储	下标计算关系，节省指针空间	完全二叉树（如堆）
带父指针的链式	左 / 右 / 父指针，支持回溯	需要频繁从子节点找父节点的场景
线索二叉树	利用空指针存前驱 / 后继，快速遍历	静态树（构建后少修改），需高效遍历

常见疑惑点再梳理

指针未初始化的问题：任何指针（左、右、父）必须初始化为NULL，否则会导致野指针错误。
内存泄漏：链式存储的节点用malloc分配，使用后必须用free释放（通常需要递归遍历释放所有节点）。
数组存储的浪费：非完全二叉树用数组存储时，空节点的位置会浪费空间，尽量避免。
线索二叉树的维护：修改节点（插入 / 删除）时，必须同步更新线索的标志位和指针，否则会破坏遍历顺序。

通过以上方式，就能在 C 语言中实现并灵活使用二叉树了。链式存储是基础，其他方式根据具体场景选择即可。

------------------

另外，在一般的算法题中，我们可能会把实际问题抽象成二叉树结构，但我们并不需要真的用 TreeNode 创建一棵二叉树出来，而是直接用类似哈希表的结构来表示二叉树/多叉树。

比方说这棵二叉树：

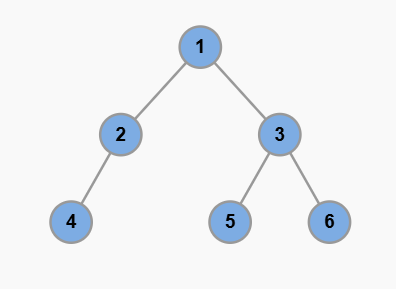
我可以用一个哈希表，其中的键是父节点 id，值是子节点 id 的列表（每个节点的 id 是唯一的），那么一个键值对就是一个多叉树节点了，这棵多叉树就可以表示成这样：

java实现

// 1 -> [2, 3]
// 2 -> [4]
// 3 -> [5, 6]HashMap<Integer, List<Integer>> tree = new HashMap<>();
tree.put(1, Arrays.asList(2, 3));
tree.put(2, Collections.singletonList(4));
tree.put(3, Arrays.asList(5, 6));

2 二叉树的递归遍历

Leetcode 30-CSDN博客

3 二叉树的层序遍历

二叉树的层序遍历（也叫广度优先遍历）是按 “层次顺序” 访问节点的方式：先访问根节点，再访问根的左右子节点，接着访问下一层的所有节点，以此类推。

核心是 “按层推进”，最经典的实现依赖队列（先进先出），但也有其他变通方式。

下面详细介绍三种实现方式，拆解每个细节和疑惑点。

先明确前提：二叉树节点定义

所有实现基于最常见的链式存储节点，定义如下（后面不再重复）：

#include <stdio.h>
#include <stdlib.h>// 二叉树节点结构
typedef struct TreeNode {int data;struct TreeNode* left;  // 左子节点struct TreeNode* right; // 右子节点
} TreeNode;// 创建新节点（辅助函数）
TreeNode* createNode(int data) {TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode));if (node == NULL) {printf("内存分配失败\n");exit(1);}node->data = data;node->left = NULL;node->right = NULL;return node;
}

方式一：队列实现（最标准、最常用）

核心思想：用队列保存 “当前层待访问的节点”，每次从队头取出一个节点访问，再将其左右子节点（若存在）入队，直到队列为空。

步骤拆解：

初始化队列，将根节点入队（若根为空，直接返回）。
循环：从队列取出队头节点，访问其值。
若该节点有左子节点，左子节点入队；若有右子节点，右子节点入队。
重复步骤 2-3，直到队列空（所有节点访问完毕）。

队列的实现（关键！）

C 语言没有现成的队列库，需要手动实现。队列需要支持：入队（尾插）、出队（头删）、判空。这里用链表实现队列（更灵活，无需预设大小）：

// 队列节点（存储二叉树节点的指针）
typedef struct QueueNode {TreeNode* treeNode;       // 存储二叉树节点struct QueueNode* next;   // 指向下一个队列节点
} QueueNode;// 队列结构（记录头和尾，方便操作）
typedef struct {QueueNode* front;  // 队头（出队用）QueueNode* rear;   // 队尾（入队用）
} Queue;// 初始化队列（空队列）
void initQueue(Queue* q) {q->front = q->rear = NULL;
}// 入队操作（从队尾添加）
void enqueue(Queue* q, TreeNode* treeNode) {// 创建队列节点QueueNode* newNode = (QueueNode*)malloc(sizeof(QueueNode));newNode->treeNode = treeNode;newNode->next = NULL;if (q->front == NULL) {  // 队列空时，头和尾都指向新节点q->front = q->rear = newNode;} else {  // 队列非空时，尾节点的next指向新节点，更新尾q->rear->next = newNode;q->rear = newNode;}
}// 出队操作（从队头取出）
TreeNode* dequeue(Queue* q) {if (q->front == NULL) {  // 队空，返回NULLreturn NULL;}// 保存队头节点QueueNode* temp = q->front;TreeNode* treeNode = temp->treeNode;  // 取出二叉树节点// 更新队头（若只有一个节点，出队后队空）if (q->front == q->rear) {q->front = q->rear = NULL;} else {q->front = q->front->next;}free(temp);  // 释放队列节点的内存return treeNode;
}// 判断队列是否为空
int isEmpty(Queue* q) {return q->front == NULL;
}

疑惑点 1：为什么队列要存TreeNode*而不是节点值？因为我们需要通过节点指针访问它的左右子节点（后续入队需要），只存值的话无法继续遍历子节点。

疑惑点 2：队列的front和rear为什么都要维护？

front用于出队（每次取队头），rear用于入队（每次加在队尾），这样入队和出队都是 O (1) 时间复杂度。
如果只维护front，入队时需要遍历到尾部，时间复杂度会变成 O (n)，效率低。

层序遍历函数（基于队列）

void levelOrderTraversal(TreeNode* root) {if (root == NULL) {  // 空树直接返回printf("树为空\n");return;}Queue q;initQueue(&q);enqueue(&q, root);  // 根节点入队while (!isEmpty(&q)) {  // 队列非空时循环TreeNode* current = dequeue(&q);  // 取出队头节点printf("%d ", current->data);     // 访问节点值// 左子节点存在则入队if (current->left != NULL) {enqueue(&q, current->left);}// 右子节点存在则入队if (current->right != NULL) {enqueue(&q, current->right);}}printf("\n");
}

示例测试：构建如下二叉树并测试：

plaintext

        1/ \2   3/ \   \4   5   6

测试代码：

int main() {// 构建示例树TreeNode* root = createNode(1);root->left = createNode(2);root->right = createNode(3);root->left->left = createNode(4);root->left->right = createNode(5);root->right->right = createNode(6);printf("层序遍历结果：");levelOrderTraversal(root);  // 输出：1 2 3 4 5 6 return 0;
}

疑惑点 3：为什么这样能保证 “按层访问”？队列的 “先进先出” 特性决定的：

第一层（根节点 1）入队，出队访问后，将第二层的 2、3 入队（队列此时是 [2,3]）。
第二层的 2 出队访问，将第三层的 4、5 入队（队列变为 [3,4,5]）；接着 3 出队访问，将 6 入队（队列变为 [4,5,6]）。
第三层的 4、5、6 依次出队访问，无更多子节点，队列空，遍历结束。每层节点按顺序入队，自然按顺序出队，实现层序。

方式二：数组模拟队列（简化版，适合已知树大小）

如果能预估树的最大节点数，可用数组模拟队列（比链表队列更简单，无需频繁 malloc），核心是用 “头指针” 和 “尾指针” 标记队列范围。

实现步骤：

定义一个数组作为队列，预设最大容量（如MAX_SIZE）。
用front记录队头下标，rear记录队尾下标（初始都为 0）。
入队：queue[rear++] = 节点；出队：return queue[front++]。
判空：front == rear。

代码实现：

#define MAX_SIZE 100  // 预设最大节点数（根据实际情况调整）void levelOrderWithArray(TreeNode* root) {if (root == NULL) {printf("树为空\n");return;}TreeNode* queue[MAX_SIZE];  // 数组模拟队列int front = 0, rear = 0;    // 队头、队尾指针queue[rear++] = root;  // 根节点入队while (front < rear) {  // 队列非空（front < rear）TreeNode* current = queue[front++];  // 出队printf("%d ", current->data);// 左子节点入队（检查是否超过最大容量）if (current->left != NULL && rear < MAX_SIZE) {queue[rear++] = current->left;}// 右子节点入队if (current->right != NULL && rear < MAX_SIZE) {queue[rear++] = current->right;}}printf("\n");
}

测试结果：和方式一完全相同（1 2 3 4 5 6）。

疑惑点 4：数组队列的front和rear为什么初始为 0？

rear指向 “下一个入队位置”，初始 0 表示第一个元素存在下标 0。
front指向当前队头元素，出队时front++，表示队头后移。
当front == rear时，队列空（所有元素已出队）。

疑惑点 5：为什么要检查rear < MAX_SIZE？数组容量固定，若树的节点数超过MAX_SIZE，rear会越界导致数组访问错误。因此这种方式只适合节点数已知且不超过预设值的场景（如题目明确树的大小）。

方式三：递归实现（不直观，但可行）

递归通常用于深度优先遍历（前 / 中 / 后序），但层序遍历也能递归实现。核心是：先获取树的深度，再按 “每层” 递归访问节点。

步骤拆解：

计算二叉树的深度（最大层数）。
从第 1 层（根节点）到第depth层，依次递归访问每一层的所有节点。
访问第k层节点的规则：若当前节点在第k层，直接访问；否则递归访问其左右子节点（子节点的层数 = 当前层数 + 1）。

辅助函数：计算树的深度

int getDepth(TreeNode* root) {if (root == NULL) {return 0;  // 空节点深度为0}// 左子树深度和右子树深度的最大值 + 1（当前节点）int leftDepth = getDepth(root->left);int rightDepth = getDepth(root->right);return (leftDepth > rightDepth ? leftDepth : rightDepth) + 1;
}

辅助函数：访问第 k 层的所有节点

void printLevel(TreeNode* root, int k) {if (root == NULL) {return;  // 空节点，直接返回}if (k == 1) {  // 当前节点在第1层（相对于当前递归的起点）printf("%d ", root->data);return;}// 递归访问下一层（k-1）printLevel(root->left, k - 1);printLevel(root->right, k - 1);
}

层序遍历函数（递归版）

void levelOrderRecursive(TreeNode* root) {if (root == NULL) {printf("树为空\n");return;}int depth = getDepth(root);  // 获取树的总深度// 从第1层到第depth层，依次访问for (int i = 1; i <= depth; i++) {printLevel(root, i);}printf("\n");
}

测试结果：同样输出1 2 3 4 5 6。

疑惑点 6：递归如何保证 “同一层” 的节点被访问？printLevel(root, k)的逻辑是：只有当k=1时才访问节点，否则递归到子节点（k-1）。例如：

访问第 1 层：printLevel(root, 1)直接访问根节点。
访问第 2 层：printLevel(root, 2)会递归到root->left和root->right，此时k=1，访问这两个节点。
访问第 3 层：递归到root->left->left、root->left->right、root->right->right，k=1时访问，正好是第 3 层节点。

疑惑点 7：递归方式的效率问题？效率较低！因为每访问一层都要从根节点重新遍历（例如访问第 k 层时，前 k-1 层的节点会被重复检查）。时间复杂度是 O (n²)（n 为节点数），而队列方式是 O (n)。因此递归方式仅作为思路拓展，实际很少用。

三种方式的对比与总结

实现方式	核心依赖	时间复杂度	空间复杂度	适用场景
链表队列	链式队列	O(n)	O(n)	通用场景（节点数不确定）
数组模拟队列	固定大小数组	O(n)	O(n)	节点数已知且较小的场景
递归实现	树的深度 + 递归	O(n²)	O(h)	理解原理（实际开发少用）

关键结论：

队列是层序遍历的 “标准工具”，链表队列最灵活，优先掌握。
数组队列适合简单场景，但要注意容量限制。
递归方式仅作思路参考，效率低，不推荐实际使用。

常见错误与注意事项

空树处理：所有方式必须先判断root == NULL，否则会访问空指针导致崩溃。
队列内存释放：链表队列在遍历结束后，若需要继续使用队列，应释放剩余节点（但遍历结束后队列已空，dequeue时已释放，无需额外操作）。
数组队列越界：若树的节点数超过MAX_SIZE，会导致数组越界，需根据实际情况调整MAX_SIZE。
递归栈溢出：对于深度极大的树（如左斜树，深度 = 节点数），递归方式可能导致栈溢出（递归深度过深）。

通过以上三种方式，就能全面掌握二叉树的层序遍历实现了。重点理解队列方式的 “先进先出” 如何匹配层序遍历的 “按层访问” 逻辑，这是核心中的核心。

4 关于c语言写二叉树

【c语言算法题做二叉树是不是比java少，我怎么觉得好像不太用这个c语言写二叉树？】

在算法题中，用 C 语言实现二叉树的频率确实可能低于 Java、Python 等语言，这背后有语言特性、实际场景和使用习惯等多方面的原因。我们可以从几个角度具体分析：

一、C 语言实现二叉树的 “门槛更高”，导致实际使用中更少

二叉树的核心是动态节点的创建、指针操作和内存管理，而 C 语言在这些方面的 “手动性” 会增加实现成本：

节点定义与创建更繁琐C 语言没有类和构造函数，必须手动定义结构体、写createNode函数（分配内存、初始化指针）。例如：

// C语言必须手动定义结构体和创建函数
typedef struct TreeNode {int val;struct TreeNode* left;struct TreeNode* right;
} TreeNode;TreeNode* createNode(int val) {TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode));if (!node) { /* 处理内存分配失败 */ }node->val = val;node->left = node->right = NULL;return node;
}

而 Java 有类和构造函数，定义更简洁：

// Java直接用类定义，构造函数初始化
class TreeNode {int val;TreeNode left;TreeNode right;TreeNode(int x) { val = x; }
}

对于算法题这种追求快速实现的场景，C 语言的 “手动操作” 会显得冗余。

内存管理需要手动处理C 语言中malloc分配的节点必须用free释放，否则会内存泄漏。虽然算法题通常不严格要求释放内存（程序运行结束后 OS 会回收），但习惯上仍需考虑（尤其是复杂逻辑中避免野指针）。而 Java 有垃圾回收机制，无需手动释放，减少了出错风险。
指针操作容易出错C 语言的指针是双刃剑：灵活但容易出现NULL指针解引用、野指针等问题（例如忘记初始化left/right为NULL，导致遍历时报错）。而 Java 中 “引用” 的空值判断更直观（if (node == null)），且没有指针算术运算，出错概率更低。

二、算法题的 “输入输出处理” 影响语言选择

二叉树类题目往往需要从输入构建树（如根据层序遍历序列构建二叉树），或将树输出为特定格式（如层序遍历序列）。这一步在 C 语言中更麻烦：

输入解析：例如 LeetCode 中输入二叉树的格式是字符串（如[1,2,3,null,null,4]），C 语言需要手动解析字符串、处理null标记、用队列构建树；而 Java 可以用内置的String.split等方法快速处理，甚至有现成的工具类辅助。
输出处理：输出遍历结果时，C 语言需要手动控制格式（如逗号分隔、括号包裹），而 Java 的StringBuilder等工具更方便。

算法题的核心是 “算法逻辑”，而非 “输入输出处理”。C 语言在这些 “辅助工作” 上的繁琐，会让开发者更倾向于选择更简洁的语言。

三、场景差异：C 语言更侧重 “底层实现”，而非 “算法题场景”

C 语言的优势在于底层控制、内存效率，适合操作系统、嵌入式等需要直接操作硬件的场景。这些场景中，二叉树的实现更注重 “空间优化”（如用数组实现完全二叉树）、“指针操作效率”，而非算法题中的 “快速编码”。

而 Java、Python 等语言更侧重 “开发效率”，适合快速实现算法逻辑。算法题的核心是考察 “对二叉树遍历、递归等思想的理解”，而非 “手动管理内存的能力”，因此这些语言更受欢迎。

四、但 C 语言对二叉树的 “底层理解” 更有帮助

虽然算法题中用 C 写二叉树较少，但学习 C 语言实现二叉树有独特价值：

更深刻理解数据结构本质：手动分配节点、维护指针关系的过程，能让你清晰知道 “二叉树的节点在内存中如何存储”“子节点和父节点如何关联”，而不是停留在 “类和引用” 的抽象层面。
为复杂数据结构打基础：后续学习红黑树、B 树等复杂结构时，C 语言的指针操作能力是必要的（这些结构的高效实现往往依赖 C 语言）。
锻炼严谨性：处理NULL指针、内存分配失败等边缘情况，能培养代码的健壮性思维。

总结

C 语言在算法题中确实较少用于实现二叉树，主要原因是手动管理节点和内存的成本高、输入输出处理繁琐，而算法题更看重 “快速实现逻辑”。

但这并不意味着 C 语言不适合二叉树 —— 相反，用 C 语言实现二叉树能帮你更深入理解其底层原理，是打好数据结构基础的重要练习。

如果目标是算法题刷题，用 Java/Python 更高效；

如果想深入掌握数据结构的本质，C 语言的练习必不可少。

5 多叉树的递归遍历（DFS）

多叉树的递归遍历（DFS）是二叉树递归遍历的自然延伸，核心区别在于：

二叉树每个节点最多 2 个子节点，遍历逻辑固定（左→右）；

而多叉树每个节点可以有任意个子节点，需要遍历所有子节点。

下面从「多叉树结构定义」开始，详细讲解 3 种递归遍历实现（前序、后序、自定义顺序），并延伸到森林的递归遍历，拆解每个细节和疑惑点。

一、多叉树的节点结构（基础中的基础）

先明确多叉树节点的定义，这是所有遍历的前提。多叉树节点需要存储「节点值」和「子节点集合」，这里用「动态数组」存储子节点（支持动态扩容，灵活应对任意数量子节点）。

#include <stdio.h>
#include <stdlib.h>// 多叉树节点结构
typedef struct MultiTreeNode {int val;                     // 节点值struct MultiTreeNode** children;  // 子节点指针数组（存储多个子节点的地址）int childCount;              // 实际子节点数量（数组中有效元素个数）int capacity;                // 子节点数组的容量（用于动态扩容）
} MultiTreeNode;

结构详解：

children：指针数组，每个元素都是MultiTreeNode*（指向一个子节点）。
childCount：记录当前有多少个子节点（遍历子节点时用它做边界判断）。
capacity：子节点数组的总容量（初始可设为 2，满了就扩容，避免越界）。

辅助函数：创建节点和添加子节点

遍历前需要先构建多叉树，因此需要两个辅助函数：

// 创建新节点（初始化值和子节点数组）
MultiTreeNode* createNode(int val) {MultiTreeNode* node = (MultiTreeNode*)malloc(sizeof(MultiTreeNode));if (!node) {printf("内存分配失败\n");exit(1);}node->val = val;node->childCount = 0;       // 初始无子节点node->capacity = 2;         // 初始容量设为2（可按需调整）node->children = (MultiTreeNode**)malloc(sizeof(MultiTreeNode*) * node->capacity);if (!node->children) {printf("子节点数组分配失败\n");free(node);exit(1);}return node;
}// 给父节点添加子节点（支持动态扩容）
void addChild(MultiTreeNode* parent, MultiTreeNode* child) {if (!parent || !child) return;  // 空指针检查（防御性编程）// 若子节点数量达到容量，扩容（容量翻倍，减少扩容次数）if (parent->childCount >= parent->capacity) {parent->capacity *= 2;  // 容量翻倍MultiTreeNode** newChildren = (MultiTreeNode**)realloc(parent->children, sizeof(MultiTreeNode*) * parent->capacity);if (!newChildren) {printf("子节点数组扩容失败\n");return;}parent->children = newChildren;  // 更新指针到新数组}// 添加子节点到数组，更新数量parent->children[parent->childCount++] = child;
}

疑惑点 1：为什么不用链表存储子节点？链表也可以存储子节点，但数组的随机访问更方便（通过下标直接访问第 i 个子节点），遍历子节点时效率更高（不需要逐个移动指针）。动态数组结合了链表的灵活性（可扩容）和数组的高效访问，是多叉树子节点存储的常用选择。

二、多叉树的递归遍历（DFS）实现

多叉树的递归遍历核心是「先访问当前节点还是先访问子节点」，由此衍生出前序和后序遍历（没有中序遍历，因为中序依赖二叉树 “左 - 根 - 右” 的固定顺序，多叉树子节点无固定顺序）。

写法一：前序遍历（根→子节点，最常用）

逻辑：先访问当前节点，再递归遍历所有子节点（按子节点数组的顺序）。

// 多叉树前序遍历：访问当前节点 → 递归遍历每个子节点
void preOrder(MultiTreeNode* root) {if (!root) return;  // 空节点直接返回（递归终止条件）// 1. 先访问当前节点printf("%d ", root->val);// 2. 再递归遍历每个子节点（按添加顺序遍历）for (int i = 0; i < root->childCount; i++) {preOrder(root->children[i]);  // 递归处理第i个子节点}
}

示例验证：构建如下多叉树（根 1 有子节点 2、3；节点 2 有子节点 4、5；节点 3 有子节点 6）：

plaintext

        1/   \2     3/ \   /4   5 6

前序遍历过程：

访问根节点 1 → 输出1；
遍历子节点 2：访问 2 → 输出2；再遍历 2 的子节点 4（访问 4 → 输出4）、5（访问 5 → 输出5）；
遍历子节点 3：访问 3 → 输出3；再遍历 3 的子节点 6（访问 6 → 输出6）。最终结果：1 2 4 5 3 6。

写法二：后序遍历（子节点→根）

逻辑：先递归遍历所有子节点，最后访问当前节点。

// 多叉树后序遍历：递归遍历每个子节点 → 访问当前节点
void postOrder(MultiTreeNode* root) {if (!root) return;  // 空节点直接返回// 1. 先递归遍历每个子节点for (int i = 0; i < root->childCount; i++) {postOrder(root->children[i]);}// 2. 再访问当前节点printf("%d ", root->val);
}

示例验证：对上述多叉树后序遍历：

遍历子节点 2：先遍历 4（输出 4）、5（输出 5），再访问 2（输出 2）；
遍历子节点 3：先遍历 6（输出 6），再访问 3（输出 3）；
访问根节点 1（输出 1）。最终结果：4 5 2 6 3 1。

疑惑点 2：子节点的遍历顺序由什么决定？由children数组的存储顺序决定。addChild函数按调用顺序将子节点存入数组（先添加的子节点在数组前面），遍历也按此顺序。例如：先给 1 添加 2，再添加 3，则遍历 1 的子节点时先处理 2，再处理 3。如果需要自定义顺序（如按值排序），可以在遍历前对children数组排序。

写法三：带深度的递归遍历（记录节点所在层次）

逻辑：在遍历过程中记录节点的深度（根为 1，子节点深度 = 父节点深度 + 1），可用于按层次筛选节点或打印层次信息。

// 带深度的递归遍历（前序为例，后序同理）
void dfsWithDepth(MultiTreeNode* root, int depth) {if (!root) return;// 访问当前节点（同时输出深度）printf("(值：%d, 深度：%d) ", root->val, depth);// 递归遍历子节点（深度+1）for (int i = 0; i < root->childCount; i++) {dfsWithDepth(root->children[i], depth + 1);}
}// 对外接口（默认根节点深度为1）
void traversalWithDepth(MultiTreeNode* root) {dfsWithDepth(root, 1);printf("\n");
}

示例结果：上述多叉树的带深度遍历结果：(值：1, 深度：1) (值：2, 深度：2) (值：4, 深度：3) (值：5, 深度：3) (值：3, 深度：2) (值：6, 深度：3)

用途：可用于判断节点是否在同一层，或按深度统计节点数量，比层序遍历更灵活（层序遍历必须按层依次处理，而递归带深度可直接访问任意层节点）。

三、森林的递归遍历（多棵多叉树的集合）

森林是多棵多叉树的集合（单棵多叉树是森林的特例）。森林的递归遍历只需遍历森林中的每棵树，再对每棵树执行多叉树的遍历逻辑。

森林的表示

用「多叉树节点指针数组」表示森林（数组每个元素是一棵多叉树的根节点）：

// 森林：多棵多叉树的根节点集合
typedef struct {MultiTreeNode** trees;  // 存储每棵树的根节点int treeCount;          // 树的数量
} Forest;// 初始化森林
Forest* createForest() {Forest* forest = (Forest*)malloc(sizeof(Forest));if (!forest) {printf("森林创建失败\n");exit(1);}forest->treeCount = 0;forest->trees = (MultiTreeNode**)malloc(sizeof(MultiTreeNode*) * 10);  // 初始容量10return forest;
}// 向森林添加一棵树
void addTreeToForest(Forest* forest, MultiTreeNode* root) {if (!forest || !root) return;// 简单处理：这里省略扩容逻辑，实际使用需添加forest->trees[forest->treeCount++] = root;
}

森林的递归遍历（前序为例）

逻辑：依次遍历森林中的每棵树，对每棵树执行前序遍历。

// 森林的前序遍历：遍历每棵树，每棵树用多叉树前序遍历
void forestPreOrder(Forest* forest) {if (!forest || forest->treeCount == 0) {printf("森林为空\n");return;}for (int i = 0; i < forest->treeCount; i++) {preOrder(forest->trees[i]);  // 对第i棵树执行前序遍历}printf("\n");
}

示例：森林包含两棵树：树 1：1 -> 2 -> 4（1 的子节点是 2，2 的子节点是 4）树 2：3 -> 5,6（3 的子节点是 5、6）森林前序遍历结果：1 2 4 3 5 6（先遍历树 1 的前序，再遍历树 2 的前序）。

四、递归遍历的核心原理与注意事项

递归三要素：
- 终止条件：if (!root) return;（空节点无需处理）。
- 当前层逻辑：访问节点（前序）或先处理子节点（后序）。
- 递归调用：遍历所有子节点，传入children[i]。
与二叉树递归的区别：二叉树遍历是left和right两个固定子节点的递归，多叉树是for循环遍历所有子节点的递归（本质是 “多分支递归”）。
可能的错误：
- 忘记检查childCount：遍历子节点时若用i < capacity而非i < childCount，会访问到未初始化的空指针（children数组中超出childCount的位置是垃圾值）。
- 递归深度过深：对于极端深的多叉树（如每个节点只有 1 个子节点，深度 = 节点数），可能导致栈溢出（C 语言栈空间有限，通常几 MB）。