组合数学 第四章 生成排列与组合

4.1 生成排列

很自然的想到递归方法：

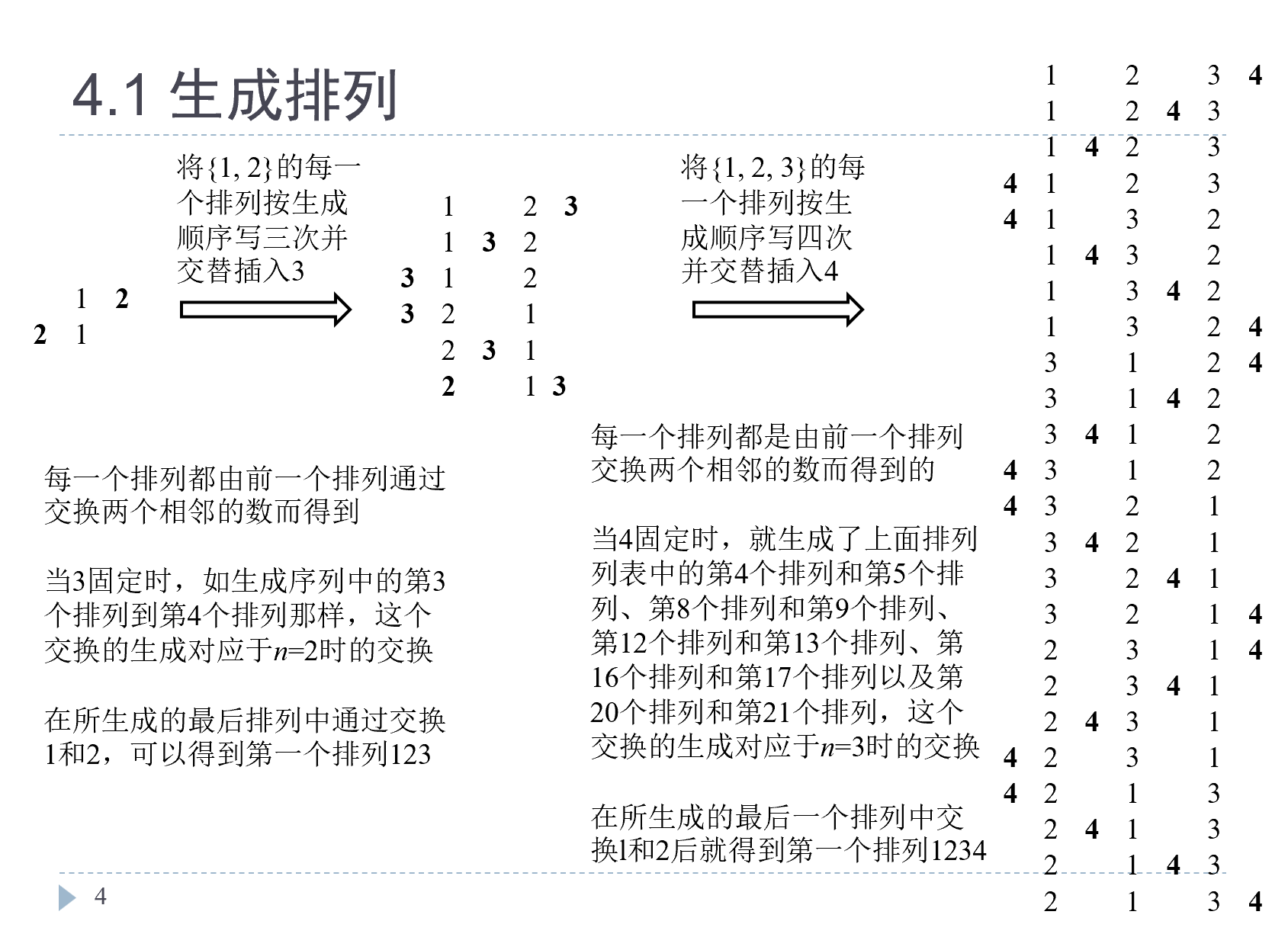
但更好的我们希望能用一个排列生成下一个排列：

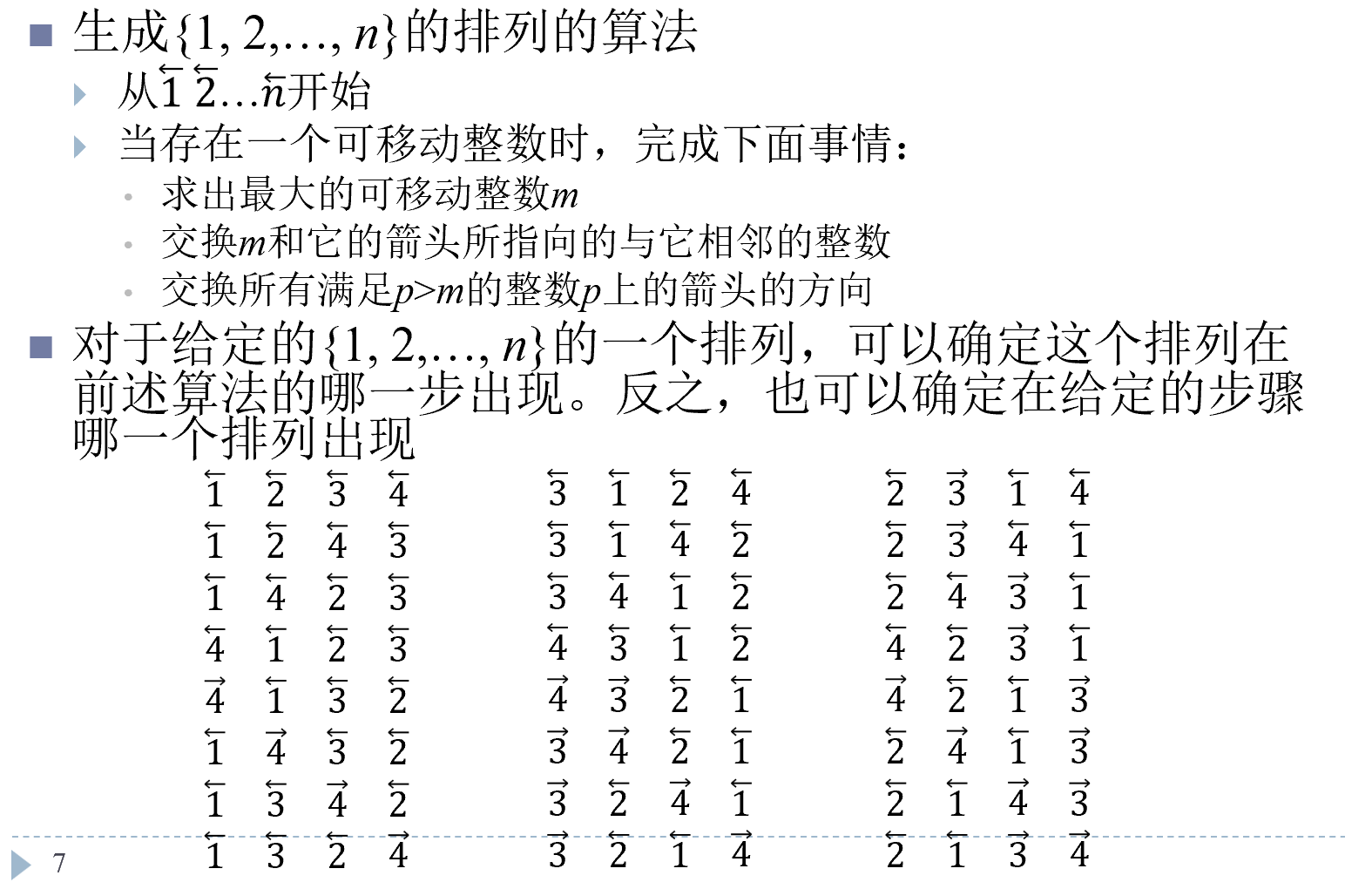
用这种标注箭头的方式，就可以用简单的交换来完成排列的生成。

4.2 排列中的逆序

逆序与你序列的概念：

4.2.1 逆序列可以构建一个排序

算法一：

算法二：

4.3 生成组合

算法一

最长用的算法就是运用二进制确定（n元组的字典序）

算法二

n元素字典序可能导致集合序列前后差别过大：

反射Gray码
从下图中可以看到这种算法的组合序存在反射关系

更形象的集合表示

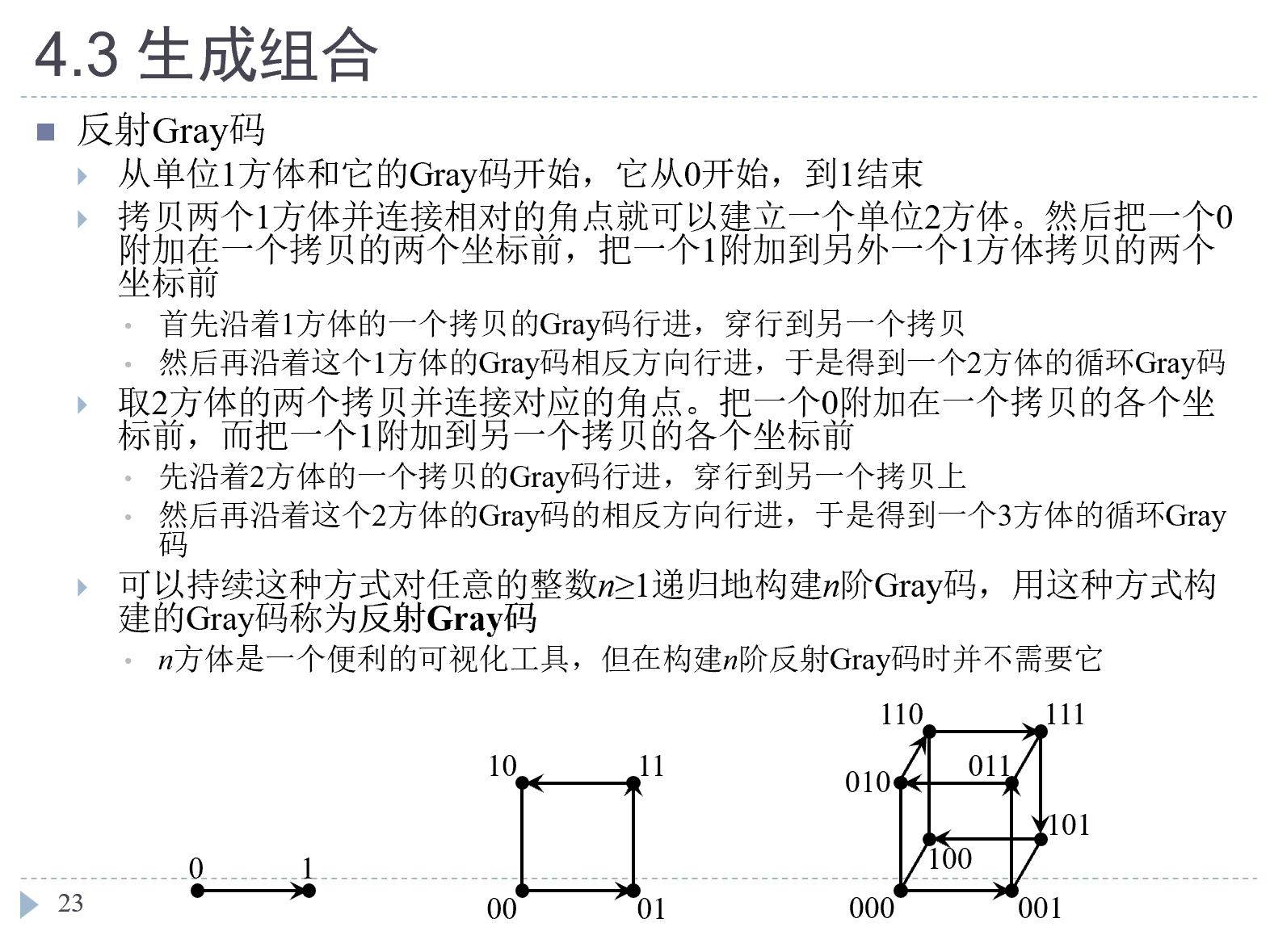
用这种方法我们能从1阶开始很容易的推出所有反射Gray码。
但是用另一种方法可以从当前的反射Gray码推出下一个
反射Gray码


对于第三点的说明：我们通过构造出了一个新的序列，可以计算n元组的字典序在反射Gray码中的位置。

4.4 生成r子集

对于字典序的r子集
求下一个子集

求一个子集在序列中的位置

4.5 偏序与等价

一些需要了解的记号和关系

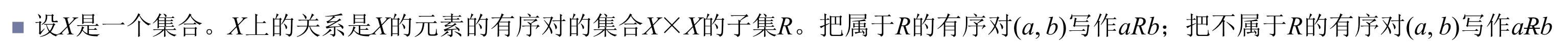
偏序

偏序与全序均是描述，集合中两个元素之间的关系

• 自反的
• 反对称的
• 传递的

除此之外

• 如果是反自反的那就是一个严格的偏序
• ⊆、≤和|均是偏序，而⊂和<是严格偏序。
• 在其上定义了偏序≤的集合X有时也叫做偏序集，记作(X, ≤)

全序

在偏序的三个性质的基础上还要是有一个完全性：
任意两个元素均能比较（即偏序的性质要在全序中任意两个元素上都有）

4.5.1

设X是有n个元素的有限集。则X上的全序与X的排列之间存在一一对应。特别地，X上不同全序的个数是n!

覆盖

设a和b是X中的元素。如果a<b并且没有元素c能够夹在a和b之间，那么称a被b覆盖，记为a<cb；就是说，不存在元素x，使得a<x和x<b同时成立。

根据定理4.5.1可知，如果(X, ≤)是全序集，则X的元素可以列成x1, x2,…, xn，使得x1<cx2<c…<cxn。正是由于这种原因，全序集也叫做线性有序集。

4.5.2

设(X, ≤)是有限偏序集，则(X, ≤)有线性扩展
什么是线性扩展：

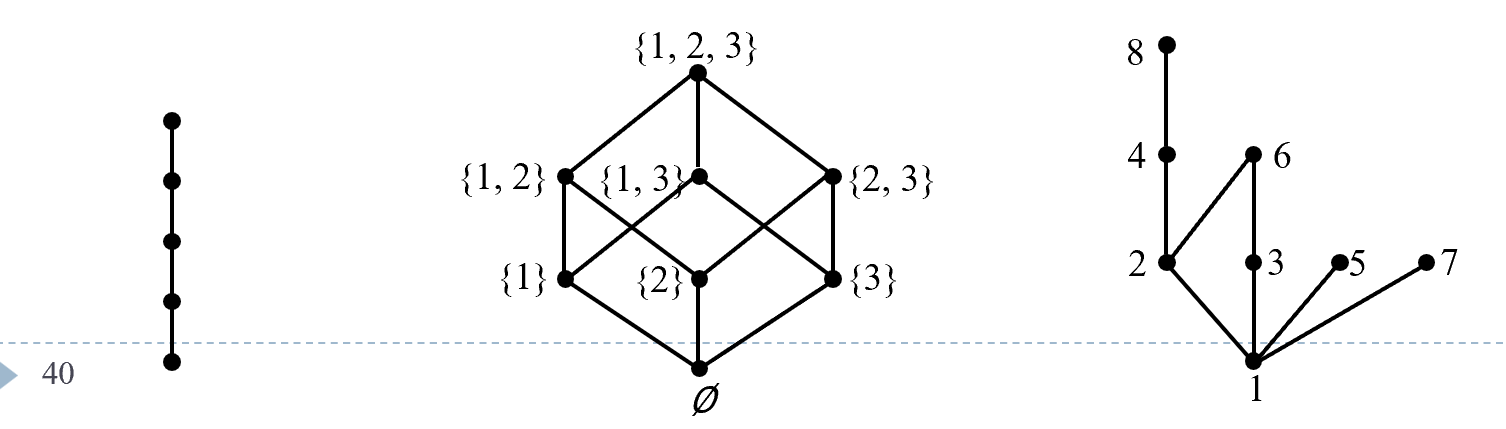
比如将上图的图3变为一条直线。

等价

典型的例子有：模 n 同余关系（整数集上的等价关系），集合像等的关系

4.5.3