数字电路 | 运放及放大器交越失真现象解析
注:本文为 “数字电路 | 运放及放大器交越失真” 相关合辑。
图片清晰度受引文原图所限。
略作重排,未整理去重。
如有内容异常,请看原文。
为什么运放会产生交越失真?
2022-04-18
作者 Luke Lu
文章来源 Cytech Engineer
有工程师反馈,使用示波器采集运放输出波形时,在特定输入电压处,原本理想的正弦波出现失真,但无法判断是运放本身还是外部因素导致。在明确工程师所用运放类型后,笔者可得出结论:该运放出现了输入交越失真现象。
多数工程师对这一现象较为陌生,甚至未听闻该术语。本文将系统完整地介绍运放的交越失真,包括其产生原因、运放基本工艺架构对交越失真的影响,以及针对交越失真的改善方法。
运放基于工艺的分类
运放基于工艺可分为 Bipolar、JFET、CMOS 三种基本架构,此外还有由上述三种衍生的 BiFET 和 CMOS zero-drift(零漂移) 架构,各类架构均有其优势。本章节将重点阐述三种基本架构。
Bipolar输入架构
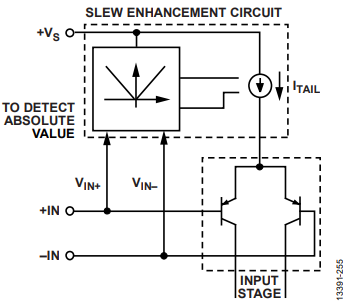
图 1 ADA4806-1 内部输入架构
上图(图 1)为 ADA4806-1 的输入架构,信号直接进入双极结型 PNP 管,属于典型的 Bipolar 架构。三极管为电流控制电流型器件,具有驱动能力强、速度快、耐压高、噪声小的特点。
由于输入极仅含一对 PNP 管,ADA4806-1 的输入电压范围仅能达到下轨。例如,在 ±5 V 供电条件下,其输入共模电压范围为 -5.1 V 至 +4 V。
JFET输入架构
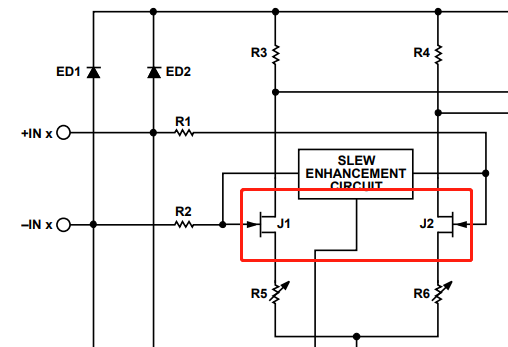
图 2 ADA4622-1 内部输入架构
上图(图 2)为 ADA4622-1 的内部输入架构,信号输入后直接进入一对 JFET 管。FET 为电压控制电流型器件,输入阻抗极高,属于电压驱动型器件,基本无需输入电流,输入回路较简单。
由于输入极仅含一对 JFET 管,ADA4622-1 的输入电压范围仅能达到下轨。例如,在 ±5 V 供电条件下,其输入共模电压范围为 -5.2 V 至 +4 V。
CMOS输入架构
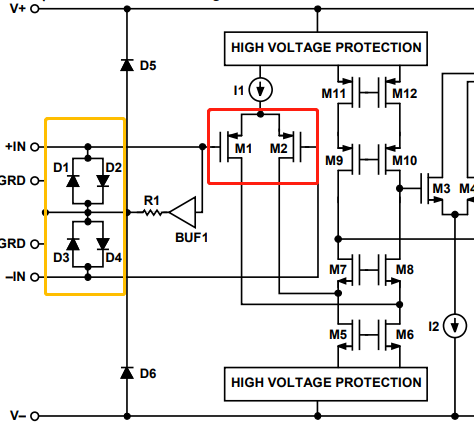
图 3 ADA4530-1 内部输入架构
上图(图 3)为 ADA4530-1 的内部输入架构,信号输入后直接进入一对 MOSFET 管。与 JFET 相同,MOSFET 也属于电压控制型器件,但输入阻抗更高,因此基于 MOSFET 的运放在失调电流和偏置电流参数上更优。
需注意,MOSFET 对静电放电(ESD)的抵抗能力较差,因此在运放电路中,其前端通常需添加二极管(如图 3 黄框所示)进行保护。此外,MOSFET 的沟道位于表面,而 JFET 的沟道位于体内,因此 JFET 输入型运放在噪声性能上更优异。
由于 ADA4530-1 输入级仅含一对 MOSFET 管,其输入电压范围仅能达到下轨。例如,在单 4.5 V 供电条件下,其输入电压范围为 0 V 至 3 V。
上述三种基本架构的介绍中,多次提及“输入电压范围”这一参数,该参数与运放的“轨到轨(Rail To Rail)”性能直接相关。轨到轨性能包括输入轨到轨和输出轨到轨,是实际应用中工程师重点关注的参数之一。
当前多数低功耗应用需低电压供电,例如 3.3 V 供电系统:若运放输入无法实现轨到轨,其输入电压动态范围会被大幅压缩。
轨到轨运放
轨到轨(Rail To Rail)运算放大器,指放大器的输入和输出电压摆幅接近或几乎等于电源电压值。
但前文所述的三种基本架构均无法真正实现轨到轨,下文将介绍两种新型架构,阐述轨到轨的实现原理。
Bipolar轨到轨输入架构
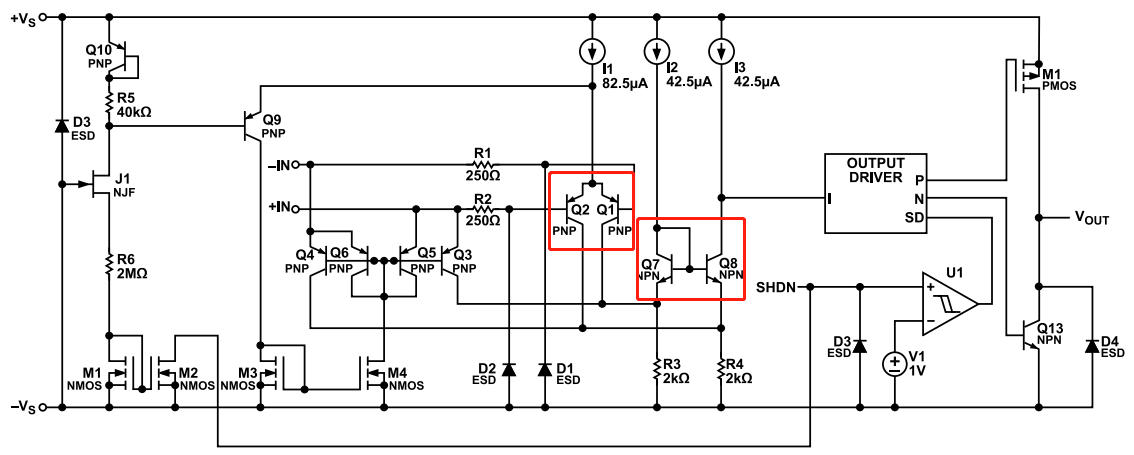
图 4 ADA4099 内部输入架构
CMOS轨到轨输入架构
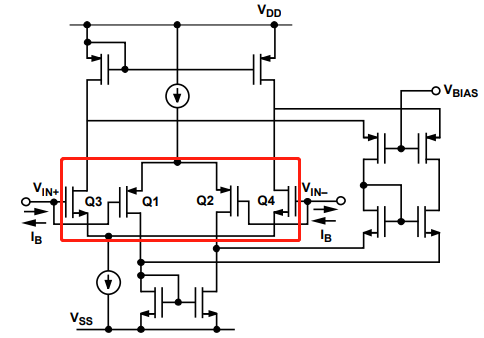
图 5 ADA4505 内部输入架构
可观察到,与前文三种非轨到轨输入架构相比,轨到轨输入运放的输入级额外增加了一对管子(无论是三极管还是 MOS 管)。
- 对于 Bipolar 型轨到轨运放:NPN 输入对可将输入电压范围扩展至接近正电源轨,PNP 输入对可将输入电压范围扩展至接近负电源轨。但受限于三极管正向放大区的工作条件,Bipolar 型运放难以绝对实现轨到轨,需保留一定裕量。
- 对于 FET 型轨到轨运放:原理与 Bipolar 型类似,但 FET 管的导通压降极低,因此输入电压范围可更接近供电电压。
运放的交越失真
由前文可知,为实现轨到轨性能,芯片设计工程师会在运放输入级采用两对极性相反的管子。实际工作中,这两对管子会交替导通;当导通状态切换时,会出现失真现象,该现象即为运放的输入交越失真。以下将通过图 6 进一步分析该现象:
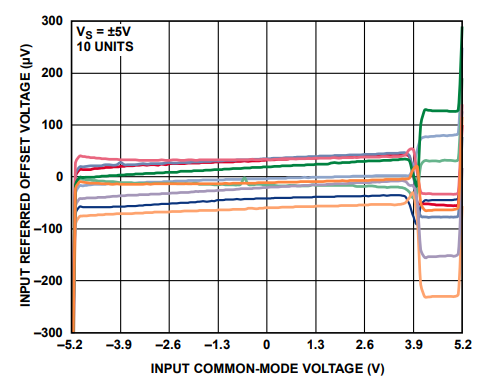
图 6 ADA4807 输入失调电压( V os V_{\text{os}} Vos)与输入共模电压关系
ADA4807 是一款支持轨到轨输入输出的高速低噪声精密运算放大器。在 ±5 V 供电条件下,当输入共模电压约为 4 V 时,其输入失调电压( V os V_{\text{os}} Vos)会出现阶跃。
这一现象可解释为:输入电压较低时,运放由 PNP 管主导工作;随着输入电压升高,NPN 管逐渐介入导通。由于两对管子的固有特性及制造工艺差异,导致输入失调电压出现阶跃,进而引发交越失真。
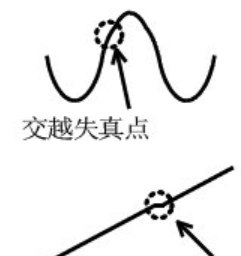
图 7 交越失真波形
上图(图 7)展示了运放交越失真的典型波形。在精密测量等对信号精度要求较高的场景中,该失真不被允许,下文将介绍交越失真的解决方法。
ADI 处理交越失真问题的解决方案
方案一:调节三极管的静态工作点
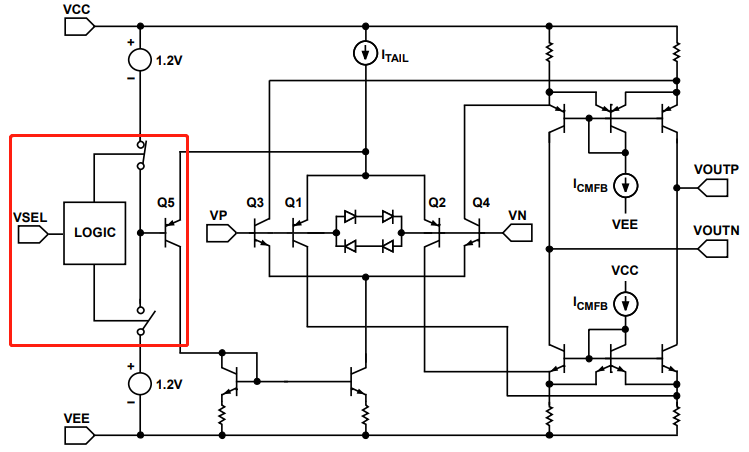
图 8 AD8027/AD8028 静态工作点调节原理
该方案并非从根本上消除交越失真,而是通过外部输入电压介入,改变三极管的静态工作点,将交越失真点向输入电压的正轨或负轨偏移。其适用场景为输入电压无需覆盖满轨范围的电路。
方案二:内置电荷泵预充电技术

图 9 AD8505 内置电荷泵消除交越失真原理
运放内部集成的电荷泵可提供一个高电压,使输入信号始终通过同一对差分管导通,无需切换至另一对管子。从原理上看,该方案可从根本上消除交越失真。
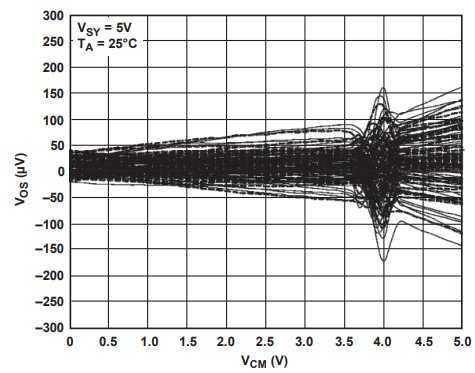
图 10 电荷泵技术改善前的 V os V_{\text{os}} Vos 与输入共模电压( V cm V_{\text{cm}} Vcm)关系
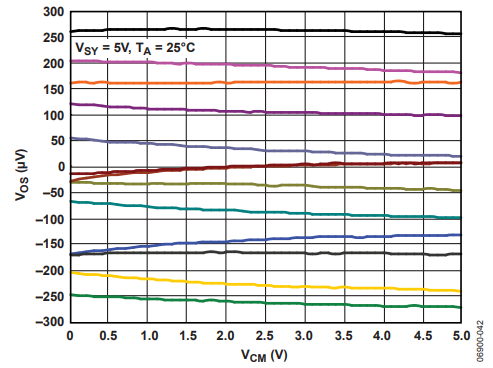
图 11 电荷泵技术改善后的 V os V_{\text{os}} Vos 与输入共模电压( V cm V_{\text{cm}} Vcm)关系
方案三:零漂移(zero-drift)架构
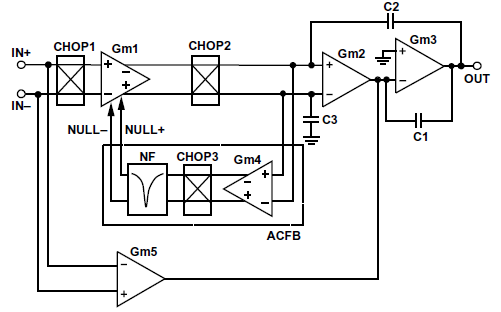
图 12 ADA4528-1 斩波(Chopping)+ 交流反馈(ACFB)架构
零漂移架构从另一角度解决交越失真:允许电路中存在交越失真,但通过内置的斩波(Chopping)和交流反馈(ACFB)电路,对失真信号进行实时校正,最终输出无失真的信号。
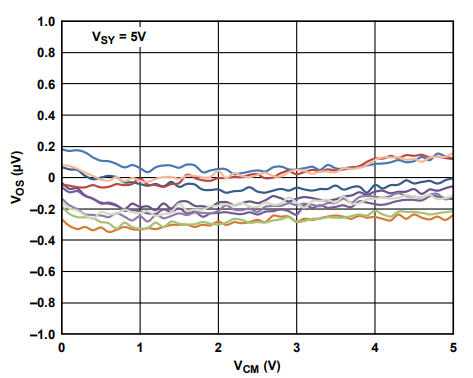
图 13 ADA4528-1 输入失调电压( V os V_{\text{os}} Vos)与输入共模电压( V cm V_{\text{cm}} Vcm)关系
总结
芯片设计中,为实现低功耗需求,工程师采用低电压供电;为扩展输入电压范围,研发出轨到轨设计;随后发现轨到轨运放的交越失真问题,并针对性提出解决方案。技术的发展始终结合实际需求,ADI 运算放大器的迭代正是在“发现问题-解决问题”的循环中推进。
通过本文阐述,可明确运放交越失真的本质,同时深入理解运放的工艺制造、芯片设计逻辑及内部器件选型思路。如需进一步了解技术细节,可点击“联系我们”提交需求,骏龙科技将提供更详细的技术支持。
参考资料
- 混合信号和数字信号处理 IC | 亚德诺半导体
- 赛尔吉欧·佛朗哥. 《基于运算放大器和模拟集成电路的电路设计》. 西安交通大学出版社.
- 毕查德·拉扎维. 《模拟CMOS集成电路设计》. 西安交通大学出版社.
放大器失真的原因解析
KK 2020-11-04 09:20:19
为使信号放大器正常工作且不导致输出信号失真,需在其基极或栅极施加特定的直流偏置。直流偏置的作用是使放大器在整个信号周期内均可放大输入信号,并将偏置“Q点”(静态工作点)设置在尽可能靠近负载线中点的位置。
偏置 Q 点的该设置对应“甲类(Class A)”放大配置,最典型的电路为双极晶体管的“共发射极电路”或单极 FET 晶体管的“共源极电路”。
放大器的功率增益、电压增益或电流增益(放大倍数),定义为输出峰值与输入峰值的比值,即 增益 = 输出峰值 输入峰值 \text{增益} = \frac{\text{输出峰值}}{\text{输入峰值}} 增益=输入峰值输出峰值。
若放大器电路设计不当(如 Q 点设置错误),或输入信号幅度过大,输出信号将无法精确复现输入信号的波形,这种现象称为“放大器失真”。以下以共发射极放大器为例,分析失真原因。
共发射极放大器

放大器失真的成因
输出信号波形失真主要源于以下三类原因:
- 偏置水平不当,导致信号周期内部分区间无法被放大;
- 输入信号幅度过大,导致放大器晶体管受电源电压限制而进入饱和/截止区;
- 放大器在输入信号的全频率范围内无法保持线性放大,即增益随频率变化。
1. 偏置差异导致的失真
共发射极或共源极晶体管电路对小幅度交流输入信号的放大效果较好,但存在一个关键问题:双极放大器 Q 点的计算位置依赖晶体管的电流放大系数 β \beta β。而相同型号晶体管的 β \beta β 值因制造公差存在差异,导致同一电路中不同晶体管的 Q 点不一致,进而引发“交越失真”。通过合理选择晶体管及偏置元件,可减小此类失真的影响。
2. 幅度失真
幅度失真是指信号波形的峰值被衰减,由 Q 点偏移导致,表现为信号周期内部分区间未被放大,其非线性波形如下所示:
偏置不当导致的幅度失真

- 若 Q 点设置在负载线下半部分(偏置不足),输出波形的负半周会“截止”或被削波;
- 若 Q 点设置在负载线上半部分(偏置过量),输出波形的正半周会“截止”或被削波。
即使 Q 点设置正确,若输入信号幅度过大,经放大器增益放大后,输出电压仍会被钳位在电源电压轨,导致波形正负半周被削波,这种幅度失真称为“削波失真”,是放大器“过驱动”的直接结果。
削波引起的幅度失真

幅度失真会显著降低放大器电路的效率:失真波形的“平顶”部分由偏置不当或输入过驱动导致,无法增强目标频率下的输出信号强度。
需注意,部分吉他手或摇滚乐队会刻意利用该特性:通过将输出波形严重钳位在正负电源轨,使声音产生强烈失真(“过度驱动”)。此外,增加正弦波的削波量可使输出波形接近“方波”,该波形可用于电子合成器或数字合成器电路。
3. 频率失真
频率失真是指放大器的增益随输入信号频率变化而产生的失真,常见于晶体管放大器中。实际应用中,放大器的输入信号通常包含“基频”(目标信号波形)和“谐波”(叠加在基频上的其他频率成分)。
正常情况下,谐波的幅度远小于基频,对输出波形影响可忽略;但若谐波幅度相对基频增大,输出波形将产生失真。例如,基频与二次谐波叠加时的频率失真如下所示:
谐波引起的频率失真

谐波频率为基频的整数倍,如二次谐波为 2 f 2f 2f、三次谐波为 3 f 3f 3f、四次谐波为 4 f 4f 4f 等。由于放大器电路中存在电容、电感等电抗元件,谐波信号的放大倍数与基频存在差异,最终导致频率失真。
4. 相位失真
相位失真(又称“延迟失真”)是指输入信号与输出信号之间存在时间延迟,由非线性晶体管放大器的频率响应差异导致。
若定义基频下输入与输出的相位差为 0,则谐波与基频之间的相位差即为相位延迟。该延迟由放大器结构决定,且随放大器带宽内的频率升高而增大。典型的相位失真波形如下所示:
延迟引起的相位失真

除高端音频放大器外,多数实际放大器均存在“幅度失真+频率失真+相位失真”的组合。在音频放大器、功率放大器等常规应用中,若失真程度较轻,通常不会影响放大器的正常工作或输出音质。
交越失真的产生原因与改善方法
IT悟物穷理IT 2016-09-11 20:29:02
交越失真的定义
在电路分析中,若忽略三极管的导通电压(实际硅管导通电压约为 0.7 V),当输入电压低于导通电压时,三极管会因截止而产生失真,该失真称为交越失真。其典型特征是失真出现在信号过零区域。
与其他放大电路类似,消除交越失真的方法是设置合理的静态工作点,使三极管在静态时处于微导通状态;当输入信号加入后,三极管可立即进入线性工作区。
交越失真的产生机理
晶体管的门限电压(导通电压)不为零,例如硅基 NPN 三极管需输入电压高于 0.7 V 才导通,硅基 PNP 三极管需输入电压低于 -0.7 V 才导通。
当输入信号为正弦波时,在 -0.7 V 至 0.7 V 的区间内,NPN 管与 PNP 管均处于截止状态,无法对信号进行放大,导致输出波形与输入波形存在差异,该差异即为交越失真。
交越失真的电路示例
产生交越失真的电路

消除交越失真的电路

交越失真的改善措施
为使三极管在静态时微导通,需提供静态偏置,具体有三种实现途径:
- 利用二极管与电阻的压降产生偏置电压,补偿三极管的导通电压;
- 利用 V BE V_{\text{BE}} VBE 扩大电路产生偏置电压,精准匹配三极管的导通特性;
- 利用电阻上的压降产生偏置电压,结构简单且成本低。
交越失真与放大电路类型的关系
- 交越失真主要出现在乙类(Class B)放大电路中:乙类电路的静态电流为 0,三极管仅在信号半个周期内导通,过零区域易因截止产生失真;
- 甲类(Class A)放大电路的失真最小,但静态电流大,效率仅约 10%;
- 甲乙类(Class AB)放大电路结合了两者优势:静态电流较小(三极管微导通),效率高于甲类,且无明显交越失真,是当前主流的放大电路类型。
LM324 系列运放交越失真的解决办法
微微一电很蒟蒻 2019-09-04 14:57:36
LM324 系列四运放芯片成本较低,广泛应用于低成本电路,但在实际使用中常出现交越失真现象。
交越失真的解决方法
将运放的输出引脚( V out V_{\text{out}} Vout)与负电源引脚( − V cc -V_{\text{cc}} −Vcc)之间串联一个 1 kΩ 或 2 kΩ 的电阻,可显著改善输出波形的交越失真。
原理分析
该现象的本质是 LM324 系列芯片的内部设计特性:为控制成本,其输入级偏置电路简化,导致轨到轨切换时易出现交越失真。串联电阻可微调输入级的静态工作点,减少管子切换时的失真。
注意事项
当运放用于波形发生电路(如正弦波振荡器、方波发生器等)时,慎用此方法。
串联电阻可能改变电路的相位裕量或增益条件,导致电路停振或无法起振。
浅谈三极管放大器失真
ujung_love 2020-06-24 01:37:45
三极管放大器的失真主要分为截止失真、饱和失真、双向失真和交越失真四类,其产生机理与电路偏置、输入信号幅度直接相关。
1. 饱和失真
- 产生机理:随着基极电流( I b I_{\text{b}} Ib)增大,集电极电流( I c I_{\text{c}} Ic)随之增大,集电极电阻( R c R_{\text{c}} Rc)上的压降增大,导致集电极-发射极电压( U ce U_{\text{ce}} Uce)减小。当 U ce U_{\text{ce}} Uce 最小降至接近 0 时, I c I_{\text{c}} Ic 不再随 I b I_{\text{b}} Ib 增大而增大;若 U ce < U be U_{\text{ce}} < U_{\text{be}} Uce<Ube(发射结导通电压), I c I_{\text{c}} Ic 不再满足 I c = β I b I_{\text{c}} = \beta I_{\text{b}} Ic=βIb,输出无法跟随输入变化,产生饱和失真。
- 波形特征:输出波形的正半周被削波(NPN 共发射极电路)。
2. 截止失真
- 产生机理:若基极电压( U b U_{\text{b}} Ub)过低,无法使发射结导通,此时 I b ≈ 0 I_{\text{b}} \approx 0 Ib≈0、 I c ≈ 0 I_{\text{c}} \approx 0 Ic≈0;即使 I b I_{\text{b}} Ib 增大, I c I_{\text{c}} Ic 仍保持接近 0 的状态,直至 U b U_{\text{b}} Ub 达到发射结导通电压,该区间内的失真称为截止失真。
- 波形特征:输出波形的负半周被削波(NPN 共发射极电路)。
3. 双向失真
- 产生机理:当输入信号幅度过大,导致三极管在信号周期内既进入饱和区(正半周),又进入截止区(负半周),这种同时存在饱和与截止的失真称为双向失真。
- 解决方法:减小输入信号幅度,或调整偏置 Q 点至负载线中点。
4. 交越失真
- 产生机理:在电路分析中,若忽略三极管的导通电压,当输入电压低于导通电压时,三极管处于截止区,无法放大信号,导致过零区域产生失真,称为交越失真。
- 适用电路:主要出现在乙类放大电路中,甲乙类放大电路可通过静态偏置消除该失真。
放大器失真类型与解决方案
一、非线性失真类型与解决方案
| 失真类型 | 产生原因 | 波形特征 | 解决方案 |
|---|---|---|---|
| 交越失真 | 轨到轨运放输入级两对极性相反的管子(如 NPN/PNP 或 NMOS/PMOS)切换时,因阈值电压差异导致信号过零点附近失真。乙类功率放大器因静态电流为零,管子在信号过零时交替截止。 | 正弦波过零区域出现“平顶”或“凹陷”,类似“削波”但仅发生在零点附近。 | 通用方法: 1. 设置静态偏置使管子微导通(如甲乙类放大器),补偿阈值电压差异。 2. 增加二极管或恒流源提供预偏置,确保管子在信号过零时持续导通。 运放专用方案: 3. 采用内置电荷泵技术(如 ADI AD8505),通过内部高压使输入信号始终通过同一对差分管,避免切换。 4. 零漂移架构(如 ADA4528-1)通过斩波和交流反馈实时校正失真。 低成本方案(如 LM324): 5. 在输出端与负电源之间串联 1kΩ~2kΩ电阻,微调静态工作点。 |
| 饱和失真 | 静态工作点(Q 点)过高,输入信号正半周使晶体管进入饱和区(VCE 接近 0),集电极电流不再随基极电流线性增加。 | 输出波形正半周被“削平”(NPN 共发射极电路),负半周被削平(PNP 共发射极电路)。 | 通用方法: 1. 增大基极电阻 Rb,降低基极电流 Ib,使 Q 点下移。 2. 减小集电极电阻 Rc,降低 Rc 上的压降,增加 VCE 裕量。 3. 提高电源电压 VCC,扩展线性放大范围。 特殊情况: 4. 若因输入信号幅度过大导致,需减小输入幅度或增加衰减电路。 |
| 截止失真 | 静态工作点过低,输入信号负半周使晶体管进入截止区(Ib≈0),集电极电流接近零。 | 输出波形负半周被“削平”(NPN 共发射极电路),正半周被削平(PNP 共发射极电路)。 | 通用方法: 1. 减小基极电阻 Rb,增大 Ib,使 Q 点上移。 2. 增加基极电源电压 VBB,提高发射结正向偏置。 3. 采用分压式偏置电路,稳定 Q 点。 特殊情况: 4. 若因输入信号幅度过大导致,需减小输入幅度或增加直流偏置。 |
| 双向失真 | 输入信号幅度过大,同时导致晶体管进入饱和区和截止区,或 Q 点设置不当且输入信号动态范围超过线性区。 | 输出波形正负半周均被削平,类似“方波”。 | 通用方法: 1. 减小输入信号幅度,确保其动态范围在放大器线性区内。 2. 重新调整 Q 点至负载线中点,平衡正负半周的放大能力。 3. 采用限幅电路或衰减器保护放大器。 |
| 不对称失真 | 电路参数不对称(如差分对管特性不一致),导致输出信号正负半周幅度或斜率不匹配。 | 输出波形正负半周不对称,如正半周幅度大于负半周或上升沿与下降沿斜率不同。 | 通用方法: 1. 选用特性匹配的差分对管或集成电路。 2. 引入负反馈(如电压并联负反馈),抑制环内非线性失真。 3. 调整偏置电阻或电流源,补偿电路不对称性。 |
二、线性失真类型与解决方案
| 失真类型 | 产生原因 | 波形特征 | 解决方案 |
|---|---|---|---|
| 幅度失真(频率失真) | 放大器对不同频率信号的增益不同,导致输出信号各频率分量的相对幅度与输入信号不一致。 | 高频信号衰减或低频信号增益过高,如音频放大器中高音不清晰或低音过重。 | 通用方法: 1. 设计宽带放大器,确保增益带宽积(GBW)满足信号带宽需求。 2. 采用频率补偿网络(如 RC 网络),均衡不同频率的增益。 3. 选择具有平坦频率响应的放大器(如宽带运放)。 |
| 相位失真(延迟失真) | 放大器对不同频率信号的相位延迟不同,导致输出信号各频率分量的相位关系与输入信号不一致。 | 多频率信号叠加后波形展宽或出现拖尾,如方波上升沿/下降沿出现振铃。 | 通用方法: 1. 优化电路布局,减少寄生电容和电感的影响。 2. 采用相位补偿技术(如超前/滞后网络),使相位响应线性化。 3. 选择相位特性良好的放大器(如低相位噪声运放)。 |
三、特殊场景解决方案
- LM324 系列运放交越失真:
- 现象:低成本运放因内部偏置简化,轨到轨切换时易出现明显交越失真。
- 方案:在输出引脚( V out V_{\text{out}} Vout)与负电源引脚( − V cc -V_{\text{cc}} −Vcc)之间串联 1kΩ~2kΩ电阻,微调静态工作点。需注意:此方法可能导致波形发生电路停振,慎用。
- 轨到轨运放交越失真:
- 现象:输入级差分对切换时,因阈值差异导致失调电压阶跃。
- 方案:
- 选择电荷泵技术运放(如 ADI AD4500),通过内部高压消除切换失真。
- 避免输入信号进入交越区域,限制输入共模电压范围。
- 单电源运放失真:
- 现象:输入信号负半周超出地电位,导致截止失真;输出信号无法达到负电源轨。
- 方案:
- 添加直流偏置(如 V cc / 2 V_{\text{cc}}/2 Vcc/2),将信号抬升至运放线性区。
- 使用耦合电容隔离直流,确保交流信号正常放大。
四、总结
- 非线性失真需通过调整静态工作点、优化电路参数或采用专用技术(如电荷泵、斩波)解决。
- 线性失真需从频率响应和相位特性入手,通过补偿网络或选择高性能器件改善。
- 低成本运放可通过外部元件(如电阻)微调,但需权衡稳定性和效率。
- 轨到轨运放需优先选择内置消除交越失真的型号(如 ADI AD8505、AD4500),以兼顾精度和动态范围。
波形发生电路中串联电阻对振荡特性的影响分析
在波形发生电路(如正弦波振荡器、方波发生器等)中,运算放大器(运放)的外部元件(电阻、电容、二极管等)需通过精确设计与计算,以满足特定振荡条件。这些振荡条件的实现依赖巴克豪森判据(Barkhausen Stability Criterion),其对电路增益与相位的严格要求决定了外部元件参数的敏感性。以下从判据内涵、串联电阻的具体影响及原理延伸展开分析,确保逻辑严谨且符合教科书式的系统性表述。
一、关键振荡条件:巴克豪森判据
巴克豪森判据是波形发生电路维持持续振荡的根本依据,需同时满足幅值条件与相位条件,二者缺一不可:
- 幅值条件:环路增益(Loop Gain)的幅值等于 1(或略大于 1)
∣ A loop ∣ = 1 ( 或 ∣ A loop ∣ ⪆ 1 ) |A_{\text{loop}}| = 1 \quad (\text{或} \ |A_{\text{loop}}| \gtrapprox 1) ∣Aloop∣=1(或 ∣Aloop∣⪆1)
振荡器需通过增益补偿反馈网络、运放输出电阻等环节克服信号损耗(如 RC 网络的衰减、元件的寄生损耗)。若环路增益幅值小于 1,振荡信号会因能量不足逐步衰减至消失;若幅值远大于 1,运放易进入饱和区,导致输出波形严重失真(如正弦波削波为方波)。
- 相位条件:环路相移(Loop Phase Shift)等于0°(或 360° 的整数倍)
ϕ loop = 0 ∘ ( 或 ϕ loop = 36 0 ∘ n , n ∈ Z ) \phi_{\text{loop}} = 0^\circ \quad (\text{或} \ \phi_{\text{loop}} = 360^\circ n, \ n \in \mathbb{Z}) ϕloop=0∘(或 ϕloop=360∘n, n∈Z)
振荡本质是正反馈过程:输出信号经反馈网络返回输入端时,需与原始输入信号同相(即总相移满足 360°),以实现信号的叠加增强。若相移偏离此范围,反馈变为负反馈,电路无法建立振荡。
二、串联电阻对振荡条件的具体影响
波形发生电路的参数设计具有极强的针对性(如电阻比值、RC/LC 网络的频率特性),串联额外电阻会直接破坏预设的增益平衡或相位平衡,导致电路停振、无法起振或波形失真。以下按电路类型分类分析:
(一)对增益条件的破坏:改变环路增益幅值
不同波形发生电路的增益需求由其拓扑结构决定,串联电阻会通过改变反馈网络衰减比或运放增益配置,打破幅值平衡。
1. 正弦波振荡器(以文氏桥振荡器为例)
文氏桥振荡器的拓扑为“RC 串并联选频网络 + 同相放大电路”,其增益匹配具有严格要求:
- 选频特性:RC 串并联网络在振荡频率 f 0 f_0 f0 下的衰减系数固定为 1 3 \frac{1}{3} 31(即反馈信号幅值为输出信号的 1 3 \frac{1}{3} 31)。
- 增益要求:为满足幅值条件,运放同相放大电路的电压增益需精确设计为 A u = 3 A_u = 3 Au=3(由反馈电阻 R f R_f Rf 与限流电阻 R 1 R_1 R1 的比值决定,即 A u = 1 + R f R 1 A_u = 1 + \frac{R_f}{R_1} Au=1+R1Rf)。
若在以下路径串联额外电阻,会直接改变增益平衡:
- 反馈通路(如 R f R_f Rf 或 R 1 R_1 R1 支路):会改变 R f R 1 \frac{R_f}{R_1} R1Rf 的比值,导致运放增益偏离 3。若增益小于 3,环路总增益幅值小于 1,振荡信号衰减至停振;若增益远大于 3,运放饱和,输出波形由正弦波削波为方波。
- RC 选频网络:会增大网络衰减系数(大于 1 3 \frac{1}{3} 31),即使运放增益仍为 3,环路总增益幅值也会小于 1,无法维持振荡。
2. 方波发生器(以施密特触发器为)
方波发生器依赖“施密特触发器的迟滞特性 + RC 充放电网络”实现振荡,其振荡逻辑与迟滞电压直接相关:
- 迟滞电压公式:
U T + = R 1 R 1 + R f U O H , U T − = − R 1 R 1 + R f U O L U_{T+} = \frac{R_1}{R_1 + R_f} U_{OH}, \quad U_{T-} = -\frac{R_1}{R_1 + R_f} U_{OL} UT+=R1+RfR1UOH,UT−=−R1+RfR1UOL
( U O H U_{OH} UOH、 U O L U_{OL} UOL 为运放输出高、低电平)。
- 振荡逻辑:RC 电容通过运放输出充电/放电,当电容电压达到 U T + U_{T+} UT+ 或 U T − U_{T-} UT− 时,施密特触发器翻转,形成方波输出。
若在迟滞电压分压支路(如 R 1 R_1 R1 或 R f R_f Rf)串联电阻:
- 会改变 R 1 R 1 + R f \frac{R_1}{R_1 + R_f} R1+RfR1 的比值,导致 U T + U_{T+} UT+ 与 U T − U_{T-} UT− 的差值(迟滞窗口)缩小甚至消失。
- 若迟滞窗口消失,施密特触发器无法实现电平翻转,运放陷入线性区,电路停振。
(二)对相位条件的破坏:改变环路相移与相位裕量
相位裕量是衡量电路振荡稳定性的关键指标(指环路相移达到 − 18 0 ∘ -180^\circ −180∘ 时,环路增益幅值对应的衰减量)。串联电阻会通过改变选频网络的相移特性,破坏 36 0 ∘ 360^\circ 360∘ 总相移要求,或降低相位裕量导致振荡不稳定。
1. RC 相移振荡器
RC 相移振荡器的拓扑为“3 节 RC 移相网络 + 反相放大电路”,其相位匹配依赖精确的 RC 参数:
- 相移特性:每节 RC 网络在特定频率下可提供约 6 0 ∘ 60^\circ 60∘ 相移,3 节网络总相移为 18 0 ∘ 180^\circ 180∘;反相放大器提供额外 18 0 ∘ 180^\circ 180∘ 相移,总相移满足 36 0 ∘ 360^\circ 360∘(相位条件)。
- 频率敏感性:RC 网络的相移与转折频率 f c = 1 2 π R C f_c = \frac{1}{2\pi RC} fc=2πRC1 紧密相关,电阻 R R R 的数值直接决定 f c f_c fc。
若在 RC 移相网络中串联额外电阻:
- 会增大 RC 网络的总电阻值,使转折频率 f c f_c fc 降低,导致在原设计振荡频率 f 0 f_0 f0 下,每节 RC 网络的相移偏离 6 0 ∘ 60^\circ 60∘,3 节总相移不再是 18 0 ∘ 180^\circ 180∘。
- 叠加反相放大器的 18 0 ∘ 180^\circ 180∘ 相移后,环路总相移偏离 36 0 ∘ 360^\circ 360∘,相位条件不满足,电路无法起振。
- 同时,串联电阻会增大 RC 网络的阻抗,改变运放的输入负载与输出负载特性,进一步恶化运放的频率响应,导致相位裕量降低,即使勉强起振也易出现波形抖动。
2. LC 振荡器(以科尔皮茨、哈特莱振荡器为例)
LC 振荡器依赖“LC 谐振网络的选频特性”实现振荡,多用于高频场景(如射频电路),其相位与幅值条件均与 LC 网络参数相关:
- 谐振特性:LC 网络在谐振频率 f 0 = 1 2 π L C f_0 = \frac{1}{2\pi\sqrt{LC}} f0=2πLC1 下的阻抗最大、相移为 0 ∘ 0^\circ 0∘,此时反馈网络仅需提供 18 0 ∘ 180^\circ 180∘ 相移(如反相放大器),即可满足总相移 36 0 ∘ 360^\circ 360∘。
- Q 值影响:LC 网络的品质因数 Q = ω 0 L R s Q = \frac{\omega_0 L}{R_s} Q=Rsω0L( R s R_s Rs 为回路等效串联电阻),Q 值越高,选频特性越尖锐,环路增益的幅值越易满足 1 的条件。
若在 LC 谐振回路中串联额外电阻:
- 会增大回路等效串联电阻 R s R_s Rs,导致 Q 值显著降低。Q 值下降会使 LC 网络的选频特性变平缓,谐振峰衰减,环路增益幅值难以达到 1,无法克服回路损耗,最终停振。
- 同时,额外电阻会引入额外相移(非谐振频率下),破坏 LC 网络在 f 0 f_0 f0 处的 0 ∘ 0^\circ 0∘ 相移特性,导致总相移偏离 36 0 ∘ 360^\circ 360∘。
(三)对运放静态特性与噪声的附加影响
串联电阻除直接破坏振荡条件外,还会通过影响运放的静态工作点与噪声水平,间接导致振荡异常:
- 输入偏置电流与失调电压的影响:
运放存在输入偏置电流 I I B I_{IB} IIB(流入输入级的静态电流),串联电阻会在电阻两端产生附加压降 U = I I B ⋅ R U = I_{IB} \cdot R U=IIB⋅R。该压降会叠加在运放输入级,破坏直流平衡,导致输入失调电压 U O S U_{OS} UOS 增大,静态工作点漂移。若漂移量过大,运放可能进入饱和区或截止区,无法正常放大反馈信号。 - 热噪声的引入:
所有电阻均会产生热噪声(约翰逊 - 奈奎斯特噪声),其噪声功率谱密度为 S V = 4 k T R S_V = 4kTR SV=4kTR( k k k 为玻尔兹曼常数, T T T 为绝对温度, R R R 为电阻值)。在波形发生电路中,串联电阻会增大电路总噪声,尤其在低幅值振荡(如微弱信号起振阶段)中,噪声可能掩盖有用反馈信号,导致振荡难以建立。
三、结论
波形发生电路的设计是“拓扑结构 - 元件参数 - 振荡条件”的精准匹配过程,每一个电阻、电容的数值均需基于巴克豪森判据计算确定,以确保增益与相位的双重平衡。因此,“串联电阻可能改变电路的相位裕量或增益条件,导致电路停振或无法起振”的表述完全成立,且是电路设计中的重要注意事项。
在实际应用中,若需调整波形发生电路参数(如频率、幅值),需通过重新计算反馈网络、选频网络的元件参数实现,而非随意串联额外电阻。任何元件修改后,均需重新验证巴克豪森判据的满足情况,确保电路振荡稳定且波形质量符合要求。
典型波形发生电路的参数计算示例
一、文氏桥振荡器(Wien Bridge Oscillator)
- 振荡频率:
f 0 = 1 2 π R C f_0 = \frac{1}{2\pi RC} f0=2πRC1
-
增益条件:非反相放大器增益需满足 A u = 1 + R f R 1 = 3 A_u = 1 + \frac{R_f}{R_1} = 3 Au=1+R1Rf=3(即 R f = 2 R 1 R_f = 2R_1 Rf=2R1)
-
选频网络: R 1 = R 2 = R R_1 = R_2 = R R1=R2=R, C 1 = C 2 = C C_1 = C_2 = C C1=C2=C
设计示例
| 参数类型 | 计算公式/设计步骤 | 示例数值(以 f 0 = 1 kHz f_0 = 1 \, \text{kHz} f0=1kHz 为例) |
|---|---|---|
| 选频网络 | 1. 选定电容 C = 0.1 μ F C = 0.1 \, \mu\text{F} C=0.1μF(标准值) 2. 计算电阻 R = 1 2 π f 0 C R = \frac{1}{2\pi f_0 C} R=2πf0C1 | R = 1 2 π × 1 0 3 × 0.1 × 1 0 − 6 ≈ 1.59 k Ω R = \frac{1}{2\pi \times 10^3 \times 0.1 \times 10^{-6}} \approx 1.59 \, \text{k}\Omega R=2π×103×0.1×10−61≈1.59kΩ |
| 增益网络 | 1. 取 R 1 = R = 1.59 k Ω R_1 = R = 1.59 \, \text{k}\Omega R1=R=1.59kΩ 2. 计算 R f = 2 R 1 R_f = 2R_1 Rf=2R1 | R f = 3.18 k Ω R_f = 3.18 \, \text{k}\Omega Rf=3.18kΩ(可选标准值 3.3 k Ω 3.3 \, \text{k}\Omega 3.3kΩ) |
| 验证条件 | 1. 环路增益幅值 ≥ 1 \geq 1 ≥1(实际取 A u = 3 A_u = 3 Au=3 以确保起振) 2. 相位裕量 ≥ 4 5 ∘ \geq 45^\circ ≥45∘ | 实测波形失真度 < 1 % <1\% <1%, 频率偏差 < 0.5 % <0.5\% <0.5% |
设计要点
- 元件选择:优先选用高精度电阻电容(如 ± 1 % \pm1\% ±1% 精度),避免温度漂移影响频率稳定性。
- 稳幅机制:可在 R f R_f Rf 支路串联热敏电阻(如 NTC),自动调节增益以防止波形削波。
二、RC 相移振荡器(RC Phase-Shift Oscillator)
- 振荡频率:
f 0 = 1 2 π R C 6 f_0 = \frac{1}{2\pi RC \sqrt{6}} f0=2πRC61
(3 节 RC 网络)
-
增益条件:放大器增益需满足 A ≥ 29 A \geq 29 A≥29(补偿 RC 网络的衰减)
-
相位条件:每节 RC 网络提供 6 0 ∘ 60^\circ 60∘ 相移,总相移 18 0 ∘ 180^\circ 180∘,叠加放大器的 18 0 ∘ 180^\circ 180∘ 相移后满足 36 0 ∘ 360^\circ 360∘ 正反馈
设计示例
| 参数类型 | 计算公式/设计步骤 | 示例数值(以 f 0 = 1 kHz f_0 = 1 \, \text{kHz} f0=1kHz 为例) |
|---|---|---|
| RC 网络 | 1. 选定电容 C = 0.01 μ F C = 0.01 \, \mu\text{F} C=0.01μF(标准值) 2. 计算电阻 R = 1 2 π f 0 C 6 R = \frac{1}{2\pi f_0 C \sqrt{6}} R=2πf0C61 | R = 1 2 π × 1 0 3 × 0.01 × 1 0 − 6 × 2.449 ≈ 6.57 k Ω R = \frac{1}{2\pi \times 10^3 \times 0.01 \times 10^{-6} \times 2.449} \approx 6.57 \, \text{k}\Omega R=2π×103×0.01×10−6×2.4491≈6.57kΩ |
| 放大器增益 | 1. 采用反相放大器配置 A = − R f R 1 A = -\frac{R_f}{R_1} A=−R1Rf 2. 取 R 1 = R = 6.57 k Ω R_1 = R = 6.57 \, \text{k}\Omega R1=R=6.57kΩ 3. 计算 R f = 29 R 1 R_f = 29R_1 Rf=29R1 | R f = 190.5 k Ω R_f = 190.5 \, \text{k}\Omega Rf=190.5kΩ(可选标准值 180 k Ω 180 \, \text{k}\Omega 180kΩ) |
| 验证条件 | 1. 环路增益幅值 ≥ 1 \geq 1 ≥1(实际取 A = 29 A = 29 A=29) 2. 相位裕量 ≥ 3 0 ∘ \geq 30^\circ ≥30∘ | 实测波形失真度 < 3 % <3\% <3%, 频率偏差 < 1 % <1\% <1% |
设计要点
- 元件匹配:3 节 RC 网络的电阻电容需严格对称,否则总相移偏离 18 0 ∘ 180^\circ 180∘,导致停振。
- 带宽限制:放大器带宽需大于 10 f 0 10f_0 10f0,避免高频增益不足影响振荡稳定性。
三、LC 科尔皮茨振荡器(Colpitts Oscillator)
- 振荡频率:
f 0 = 1 2 π L ⋅ C 1 C 2 C 1 + C 2 f_0 = \frac{1}{2\pi \sqrt{L \cdot \frac{C_1 C_2}{C_1 + C_2}}} f0=2πL⋅C1+C2C1C21
(串联电容分压反馈)
-
反馈条件:反馈系数 B = C 1 C 2 B = \frac{C_1}{C_2} B=C2C1,需满足 B ≈ 1 3 B \approx \frac{1}{3} B≈31 以确保稳定振荡
-
相位条件:LC 网络在谐振频率处相移为 0 ∘ 0^\circ 0∘,放大器提供 18 0 ∘ 180^\circ 180∘ 相移,总相移 18 0 ∘ 180^\circ 180∘ 满足正反馈
设计示例
| 参数类型 | 计算公式/设计步骤 | 示例数值(以 f 0 = 10 kHz f_0 = 10 \, \text{kHz} f0=10kHz 为例) |
|---|---|---|
| LC 网络 | 1. 选定电感 L = 10 mH L = 10 \, \text{mH} L=10mH(标准值) 2. 取反馈系数 B = C 1 C 2 = 1 10 B = \frac{C_1}{C_2} = \frac{1}{10} B=C2C1=101 3. 计算总电容 C T = C 1 C 2 C 1 + C 2 = 1 ( 2 π f 0 ) 2 L C_T = \frac{C_1 C_2}{C_1 + C_2} = \frac{1}{(2\pi f_0)^2 L} CT=C1+C2C1C2=(2πf0)2L1 | C T = 1 ( 2 π × 1 0 4 ) 2 × 0.01 ≈ 25.3 nF C_T = \frac{1}{(2\pi \times 10^4)^2 \times 0.01} \approx 25.3 \, \text{nF} CT=(2π×104)2×0.011≈25.3nF 设 C 1 = 2.53 nF C_1 = 2.53 \, \text{nF} C1=2.53nF,则 C 2 = 10 C 1 = 25.3 nF C_2 = 10C_1 = 25.3 \, \text{nF} C2=10C1=25.3nF |
| 验证条件 | 1. 环路增益幅值 ≥ 1 \geq 1 ≥1(通过晶体管增益补偿) 2. 相位裕量 ≥ 4 5 ∘ \geq 45^\circ ≥45∘ | 实测波形失真度 < 2 % <2\% <2%, 频率偏差 < 0.8 % <0.8\% <0.8% |
设计要点
- 元件寄生参数:高频场景下需考虑电感的直流电阻(DCR)和电容的等效串联电阻(ESR),避免损耗过大导致停振。
- 稳频措施:可在 LC 网络中串联微调电容(如 10 pF 10 \, \text{pF} 10pF),实现频率精细调节。
四、对比总结
| 电路类型 | 频率范围 | 波形质量 | 元件复杂度 | 典型应用场景 |
|---|---|---|---|---|
| 文氏桥振荡器 | 音频段(20 Hz~20 kHz) | 高(失真度 < 1 % <1\% <1%) | 低 | 音频信号源、仪器校准 |
| RC 相移振荡器 | 音频段(100 Hz~100 kHz) | 中(失真度 < 3 % <3\% <3%) | 中 | 简单振荡电路、工业控制 |
| LC 科尔皮茨振荡器 | 射频段(30 kHz~30 MHz) | 高(失真度 < 2 % <2\% <2%) | 中 | 无线通信、射频信号源 |
五、注意事项
- 元件容差:实际参数需根据元件精度调整,例如电阻电容的 ± 5 % \pm5\% ±5% 容差可能导致频率偏差 ± 10 % \pm10\% ±10%。
- 电源稳定性:纹波较大的电源会引入调制噪声,建议采用线性稳压器或 LC 滤波电路。
- 布局布线:高频电路需缩短元件引脚,避免长导线引入寄生电感电容,影响相位条件。
via:
- 为什么运放会产生交越失真?
https://www.macnicacytech.com/apac/cytech/zh/technical-articles/why-do-op-amps-produce-crossover-distortion/ - 关于放大器失真的原因你了解多少呢?
https://bbs.elecfans.com/jishu_2004685_1_1.html - 交越失真及产生原因和改善方法_功放交越失真产生原因 - CSDN 博客
https://blog.csdn.net/qq_24373811/article/details/52506158 - LM324 系列运放交越失真的解决办法_lm324 交越失真 - CSDN 博客
https://blog.csdn.net/qq_30205523/article/details/100539035 - 三极管放大器失真解析 - CSDN 博客
https://blog.csdn.net/ujung_love/article/details/106935665 - ……
