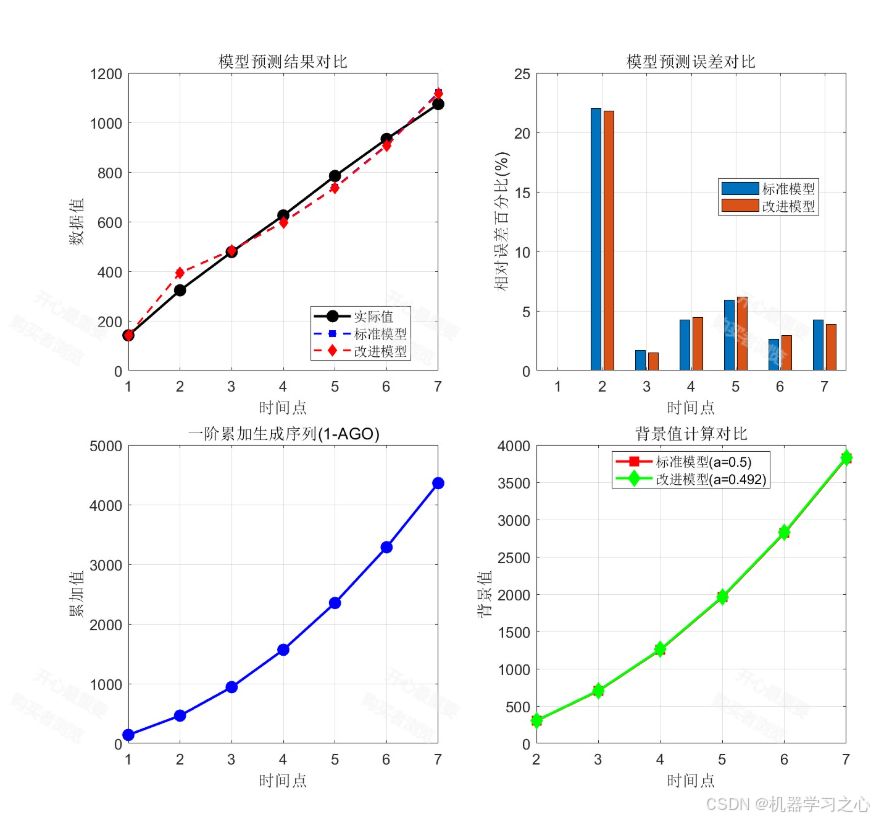
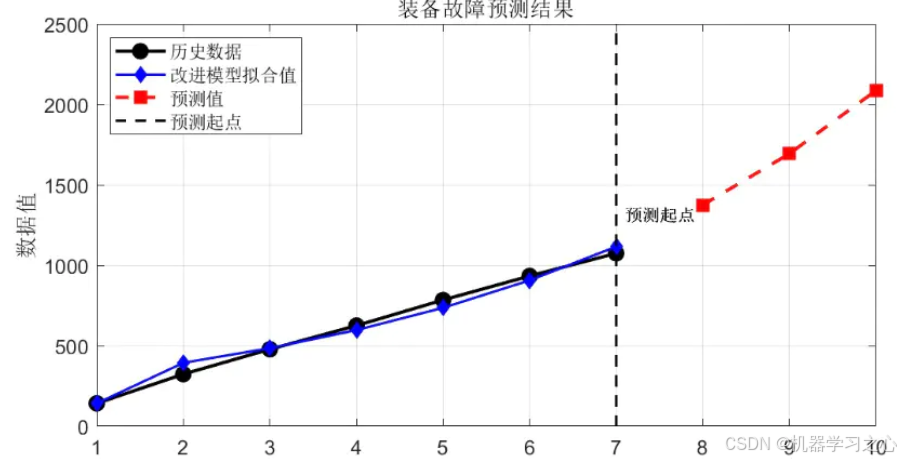
MATLAB基于混合算法改进灰色模型的装备故障预测

---

1. 核心理念：为什么要混合？

传统灰色模型（GM(1,1)）的优缺点：

• 优点：
  • 所需数据量少（通常只需4个以上数据即可建模）。
  • 不考虑数据的概率分布。
  • 计算简单，适用于趋势预测。
• 缺点：
  • 背景值构造固定：传统背景值公式 (z(1)(k) = 0.5x(1)(k) + 0.5x(1)(k-1)) 不一定是最优的，影响了模型精度。
  • 初始值依赖：模型使用第一个数据作为初始值，但理论上序列的最后一个数据包含最多信息。
  • 参数固定：发展系数 a 和灰色作用量 b 通过最小二乘法一次性确定，无法自适应优化。
  • 对波动数据敏感：对于具有较强波动性、非单调性的序列，预测效果较差。

混合算法的目的：
利用其他算法的优势来弥补灰色模型的上述缺点，从而提高预测精度和模型鲁棒性。

---

2. 常见的混合算法改进策略

混合改进主要围绕优化灰色模型的 “参数” 和 “结构” 两方面展开。

• 具体做法：
  1. 将背景值公式重构为 z(1)(k) = α * x(1)(k) + (1-α) * x(1)(k-1)，其中 α 为待优化的背景值系数（不再固定为0.5）。
  2. 将初始值不再固定为 x(0)(1)，而是设为 x(1)(1) = β，β 也为待优化参数。
  3. 构建优化问题：以 平均相对误差（MAPE） 或 均方根误差（RMSE） 最小化为目标函数。
  4. 使用GA、PSO等算法寻找最优的 α 和 β。
• 模型名称： 例如，PSO-GM(1,1)模型，GA-GM(1,1)模型。

---

3. 一个详细的实例：HHO-PSO优化灰色模型（HHO-PSO-GM(1,1)）用于轴承振动趋势预测

背景： 通过监测某装备轴承的振动加速度数据，预测其未来时间点的振动水平，以判断是否需要进行维护。

步骤：

第1步：数据准备
收集轴承从正常到故障一段时间内的振动加速度数据序列 X(0)。
X(0) = (x(0)(1), x(0)(2), ..., x(0)(n))，例如 n=10。

第2步：建立标准GM(1,1)模型框架

1. 一次累加生成（1-AGO）：X(1) = (x(1)(1), x(1)(2), ..., x(1)(n))，其中 x(1)(k) = Σx(0)(i), i=1 to k。
2. 灰微分方程：x(0)(k) + a * z(1)(k) = b。
3. 背景值重构：z(1)(k) = α * x(1)(k) + (1-α) * x(1)(k-1)。
4. 初始值重构：x(1)(1) = β。
5. 参数求解：最小二乘法解 [a, b]^T = (B^T B)^-1 B^T Y，其中矩阵 B 和 Y 由重构后的 z(1)(k) 和 β 构成。
6. 时间响应式：x^(1)(k) = (β - b/a) * exp(-a*(k-1)) + b/a。
7. 还原预测值：x^(0)(k) = x^(1)(k) - x^(1)(k-1)。

第3步：定义HHO-PSO目标函数

1. 优化参数：位置表示为 [α, β]。
2. 搜索空间：α ∈ [0, 1], β ∈ [min(X(0)), max(X(0))]。
3. 目标函数（适应度函数）：f(α, β) = MAPE = (1/n) * Σ | (x^(0)(i) - x(0)(i)) / x(0)(i) | * 100%。
   • 对于每个粒子代表的 [α, β]，都代入第2步的框架中计算一次GM(1,1)模型，并得到预测序列，然后计算其与真实序列的MAPE。MAPE越小，该粒子位置越好。

第4步：执行优化

1. 初始（随机生成一组 [α, β]）。
2. 迭代优化：
   • 计算的适应度（MAPE）。
   • 更新个体最优位置和全局最优位置。
   • 根据速度和位置更新公式，更新所有粒子的位置。
3. 终止条件：达到最大迭代次数或适应度值小于某个阈值。
4. 输出：全局最优参数 [α_opt, β_opt]。

第5步：利用优化后的模型进行预测
将 α_opt 和 β_opt 代入第2步建立的GM(1,1)模型框架中，重新计算模型参数 a 和 b，并利用时间响应式对未来 n+1, n+2, ... 时刻的装备状态进行预测。

第6步：模型评估与应用

• 计算预测结果的均方根误差（RMSE）、平均绝对误差（MAE）等指标，并与传统GM(1,1)模型对比，验证改进效果。
• 当预测的振动值超过预设的安全阈值时，系统发出预警，提示进行装备维护。

---

4. 总结与展望

特性	传统GM(1,1)	混合算法改进GM(1,1)
数据需求	少	少
模型精度	一般，对背景值敏感	高，通过优化自适应
鲁棒性	较弱，怕波动	强，能处理一定波动
计算复杂度	低	中/高（取决于混合算法）
适用性	简单趋势预测	复杂、高精度故障预测

未来研究方向：

• 与深度学习结合：例如利用LSTM捕捉长期依赖，再用优化后的灰色模型进行趋势修正。
• 多变量建模：发展MGM(1,N)模型并与优化算法结合，考虑多个故障特征参数。
• 在线学习：使模型能够随着新数据的到来而动态更新参数，实现自适应预测。
• 与物理模型融合：将数据驱动的灰色模型与装备的物理失效模型相结合，实现机理与数据的统一。

完整源码私信MATLAB基于混合算法改进灰色模型的装备故障预测