15.搜索二叉树(一)

一.内容安排说明

二. 二叉搜索树

1.二叉搜索树概念

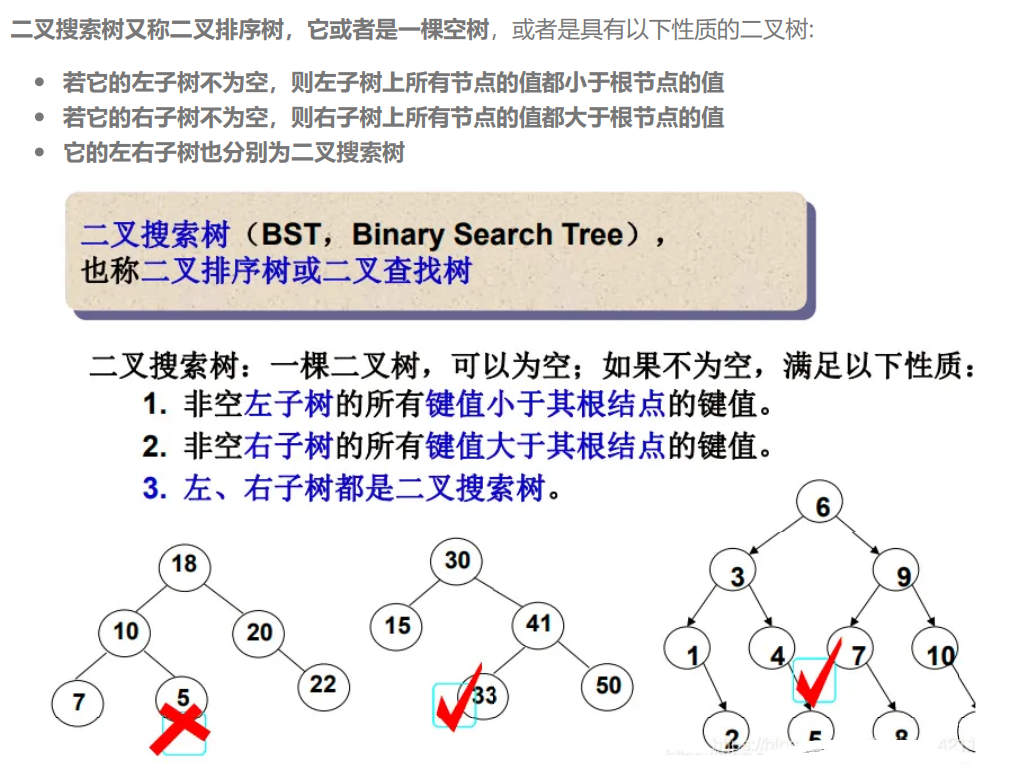
2.二叉搜索树操作

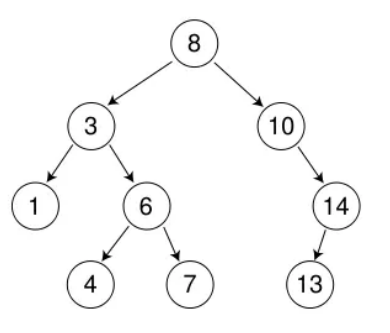
三.搜索二叉树的实现

1.搜索二叉树的定义

#pragma oncetemplate<class K>
struct BSTNode
{K _key;BSTNode<K>* _left;BSTNode<K>* _right;BSTree(const K& key):_key(key),_left(nullptr),_right(nullptr){}
};template<class K>
class BSTree
{typedef BSTNode<K> Node;
public:
private:Node* root = nullptr;
};

2.搜索二叉树的查找(Find())

bool Find(const K& key){Node* cur = _root;while(cur){if(cur->_key < key){cur = cur->_right;}else if(cur->_key > key){cur = cur->_left;}else{return true;}}return false;}

找到就返回true,没找到就返回false

3.搜索二叉树的插入(Insert())

因为我们有cur节点(root),我们根据搜索二叉树的性质进行插入(我们可以复用Find())

bool Insert(const K& key){Node* parent = nullptr;Node* cur = _root;while(cur){if(cur->_key < key){parent = cur;cur = cur->_right;}else if(cur->_key > key){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(key);if(parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}

搜索二叉树无法插入我们的重复的值

所以,搜索二叉树可以进行以下三种功能:

1.查找   2.去重  3.排序

搜索二叉树增删查改的时间复杂度是O(n)

搜索二叉树默认是不支持修改的(但是变种可以进行修改)

4.中序遍历

void InOrder(){_InOrder(_root);}
private://左 中 右void _InOrder(Node* root){if(root == nullptr){return;}_Inorder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}

外面要调用的话,我们就套一层壳

四.搜索二叉树的删除

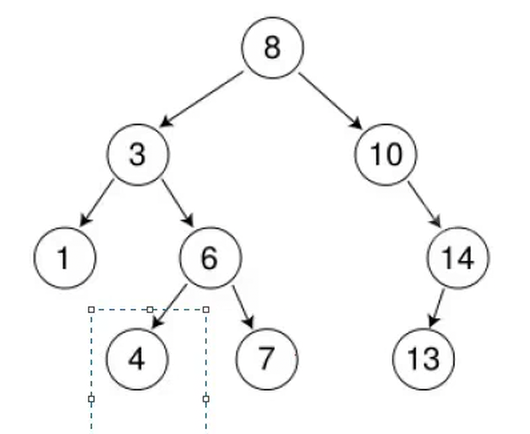
1.叶子节点

直接删除就行了,然后将原来的位置置空

2.单叶子节点

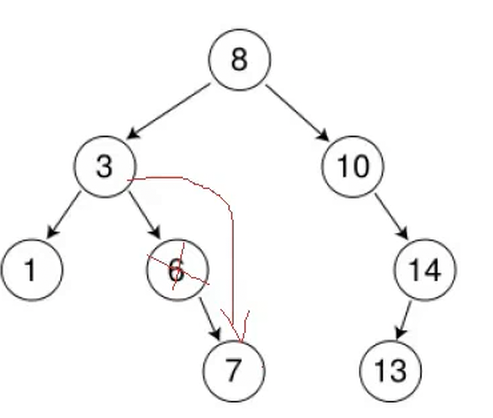
直接将自己的孩子,交给父亲节点即可

3.双孩子节点

要保证我们的二叉树的特性,那么就要找左子树的最大,或者右子树的最小

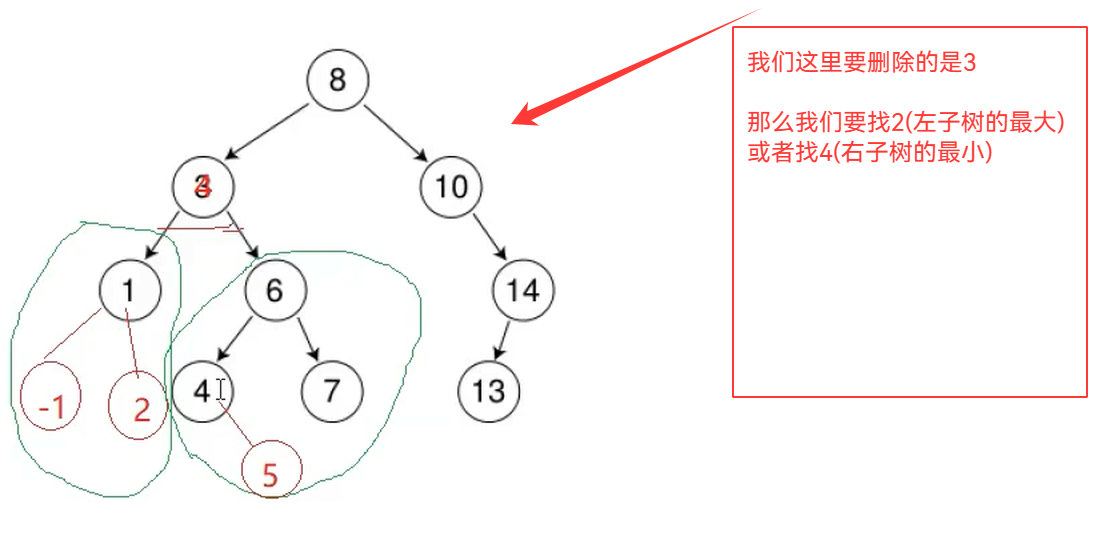
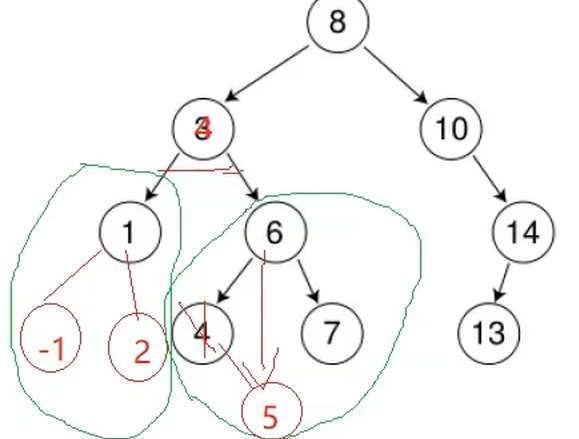
4.总结

我们可以将前两种删除方式看作是一种方式,然后最好一种为另一种方式

五.二叉搜索树删除的实现

大逻辑bool Erase(const K& key){Node* cur = _root;while(cur){if(cur->_key < key){cur = cur->_right;}else if(cur->_key > key){cur = cur->_left;}else{//删除return true;}}return false;}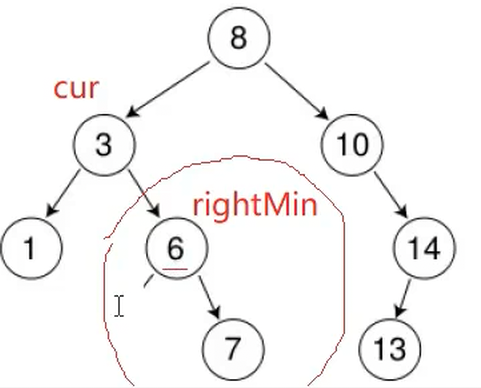

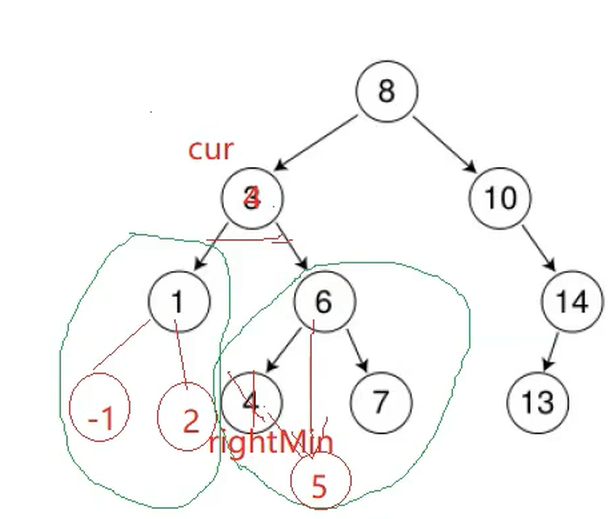
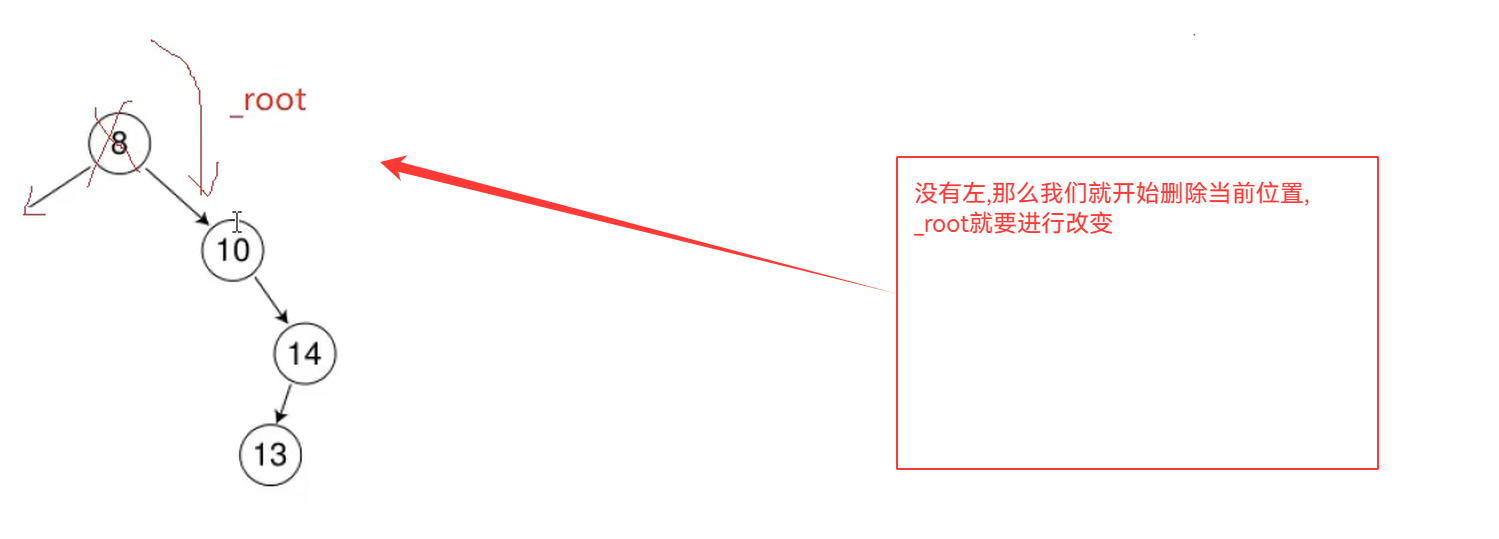
bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while(cur){if(cur->_key < key){parent = cur;cur = cur->_right;}else if(cur->_key > key){parent = cur;cur = cur->_left;}else{//删除//0 - 1 个孩子if(cur->_left == nullptr){if(parent == nullptr){_root = cur->_right;}else{if(parent->_left == cur){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}delete cur;return true;}else if(cur->_right == nullptr){if(parent == nullptr){_root = cur->_left;}else{if(parent->_left == cur){parent->_left = cur->_left;}else{parent->_right = cur->_left;}} delete cur;return true;}else{//2个孩子//右子树最小节点作为替代节点Node* rightMinP = cur;Node* rightMin= cur->_right;while(rightMin->_left){rightMinP = rightMin;rightMin = rightMin->_left;}cur->_key = rightMin->_key;if(rightMinP->_left == rightMin){rightMinP->_left = rightMin->_right;}else{rightMinP->_right = rightMin->_right;}delete rightMin;return true;}}}return false;}