第8章 基于表格型方法的规划和学习(4) 期望更新与采样更新

期望更新与采样更新

价值函数更新

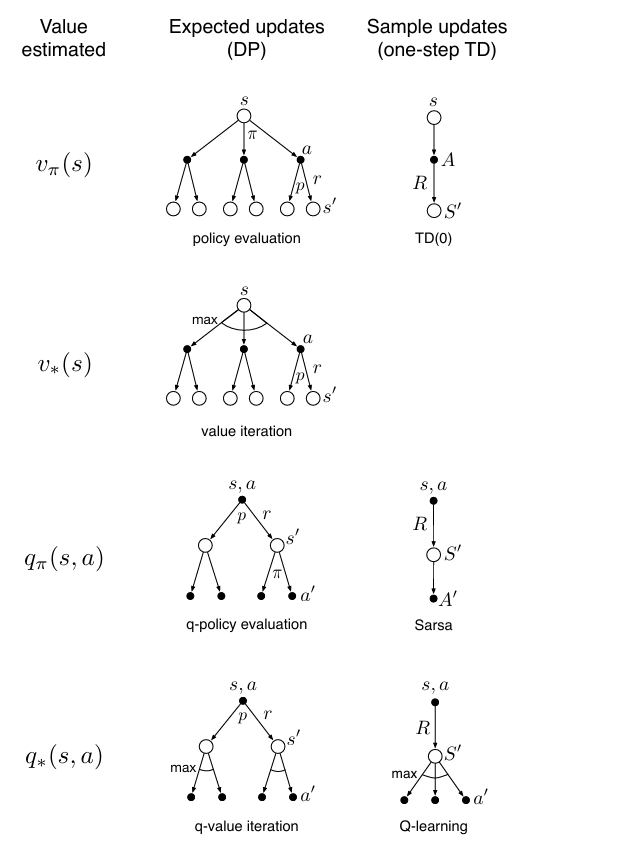
价值函数更新是强化学习中的核心操作。在强化学习中，单步更新方法可以从三个维度进行区分：更新对象（状态价值 $v$ 或动作价值 $q$）、目标策略（给定策略 $\pi$ 或最优策略 $\ast$）、以及更新方式（期望更新或采样更新）。这三个维度组合出八种可能情形，其中七种对应实际存在的算法，广泛用于学习或规划；唯一被排除的是对最优状态价值 $v_{\ast }$ 的采样更新，因其在单步采样框架下难以实现。

[!NOTE]

$v_{\pi }$ 的期望更新

这种方法用于在已知环境模型的前提下，评估一个给定策略 $\pi$ 的状态价值函数。它对应于动态规划中的策略评估过程。更新时，利用模型 $\hat{p}(s^{\prime },r\mid s)$ 对所有可能的后继状态和奖励进行加权平均，计算贝尔曼期望备份：

$$V(s)\leftarrow \sum _{s^{\prime },r}\hat{p}(s^{\prime },r\mid s)\left[r+\gamma V(s^{\prime })\right]$$

该方法完全依赖模型，属于同策略、基于模型的状态价值更新，常用于规划场景。

[!NOTE]

$v_{\pi }$ 的采样更新

当环境模型未知时，可通过与环境交互获得采样轨迹，并以此更新状态价值。这类方法包括蒙特卡洛（MC）方法和时序差分 TD(0)。其中 TD(0) 使用单步回报进行增量更新：

$$V(s)\leftarrow V(s)+\alpha [R_{t+1}+\gamma V(S_{t+1})-V(s)]$$

这里 $R_{t+1}$ 和 $S_{t+1}$ 是从环境中采样得到的。该更新无需模型，仅依赖经验，属于同策略、无模型的状态价值学习方法。

[!NOTE]

$v_{\ast }$ 的期望更新

该方法用于直接求解最优状态价值函数，对应于动态规划中的价值迭代（Value Iteration）。它利用模型对每个状态的所有可能动作进行评估，并取最大值作为更新目标：

$$V(s)\leftarrow \underset{a}{\max }\sum _{s^{\prime },r}\hat{p}(s^{\prime },r\mid s,a)\left[r+\gamma V(s^{\prime })\right]$$

虽然不显式维护策略，但每次更新都隐含一次策略改进。该方法属于基于模型、面向最优策略的状态价值规划。

[!NOTE]

被排除的情形：$v_{\ast }$ 的采样更新

理论上可以设想对最优状态价值 $v_{\ast }$ 进行单步采样更新，但实际中不可行。原因在于要获得从状态 $s$ 出发的最优转移 $(s^{\prime },r)$，必须知道在 $s$ 下应执行哪个动作，即需要知道最优策略 ${\pi }_{\ast }$。然而，若已知 ${\pi }_{\ast }$，则可以直接使用 $q_{\ast }$ 并通过 $v_{\ast }(s)={\max }_a{q}_{\ast }(s,a)$ 间接得到状态价值。因此，不存在独立、实用的 $v_{\ast }$ 单步采样更新算法，该组合通常被排除在标准分类之外。

[!NOTE]

$q_{\pi }$ 的期望更新

这是对动作价值函数 $q_{\pi }$ 的基于模型的评估方法，也属于动态规划范畴。给定策略 $\pi$ 和模型 $\hat{p}(s^{\prime },r\mid s,a)$，更新时对所有可能的转移结果求期望，并根据策略 $\pi$ 选择下一动作：

$$Q(s,a)\leftarrow \sum _{s^{\prime },r}\hat{p}(s^{\prime },r\mid s,a)\left[r+\gamma \sum _{a^{\prime }}\pi (a^{\prime }\mid s^{\prime })Q(s^{\prime },a^{\prime })\right]$$

或者等价地写作：

$$Q(s,a)\leftarrow \sum _{s^{\prime },r}\hat{p}(s^{\prime },r\mid s,a)\left[r+\gamma Q(s^{\prime },a^{\prime })\right],\text{其中 }{a}^{\prime }\sim \pi (\cdot \mid s^{\prime })$$

该方法显式依赖策略 $\pi$，适用于模型已知的规划任务。

[!NOTE]

$q_{\pi }$ 的采样更新

这是SARSA算法的核心更新规则。在无模型设置下，智能体执行策略 $\pi$，观察到状态-动作-奖励-下一状态-下一动作序列 $(S,A,R,S^{\prime },A^{\prime })$，并据此更新动作价值：

$$Q(s,a)\leftarrow Q(s,a)+\alpha [R+\gamma Q(S^{\prime },A^{\prime })-Q(s,a)]$$

其中 $A^{\prime }$ 是根据当前策略 $\pi$ 在 $S^{\prime }$ 中选择的动作。SARSA 是典型的同策略、无模型、动作价值学习算法。

[!NOTE]

$q_{\ast }$ 的期望更新

这是对最优动作价值函数 $q_{\ast }$ 的基于模型的迭代方法，有时称为Q-值动态规划或精确 Q-iteration。更新规则直接实现贝尔曼最优方程：

$$Q(s,a)\leftarrow \sum _{s^{\prime },r}\hat{p}(s^{\prime },r\mid s,a)\left[r+\gamma \underset{a^{\prime }}{\max }Q(s^{\prime },a^{\prime })\right]$$

该方法无需显式策略，最优策略可由 ${\pi }_{\ast }(s)=\arg {\max }_{a}Q(s,a)$ 直接导出，属于基于模型、面向最优策略的动作价值规划。

[!NOTE]

$q_{\ast }$ 的采样更新

这是Q-learning算法的更新规则，也是最著名的无模型离策略算法。它通过采样经验更新动作价值，目标是逼近最优动作价值函数：

$$Q(s,a)\leftarrow Q(s,a)+\alpha [R+\gamma \underset{a^{\prime }}{\max }Q(S^{\prime },a^{\prime })-Q(s,a)]$$

关键在于，更新目标使用 ${\max }_{a^{\prime }}Q(S^{\prime },a^{\prime })$，而非行为策略实际选择的动作。因此，Q-learning 可以在执行任意行为策略的同时学习最优策略，属于离策略、无模型、动作价值学习方法。

案例：用于近似最优动作价值函数 $Q^{\ast }$

在强化学习中，更新价值函数的方式主要分为两类：期望更新和采样更新。二者的核心区别在于是否利用环境的完整模型，以及是否对所有可能的后续结果进行平均。

期望更新

期望更新假设我们拥有一个准确的环境模型 $\hat{p}(s^{\prime },r\mid s,a)$，该模型给出了在状态 $s$ 执行动作 $a$ 后，转移到状态 $s^{\prime }$ 并获得奖励 $r$ 的概率。利用这一模型，期望更新会对所有可能的后继状态和奖励进行加权平均，从而执行一次完整的贝尔曼备份。

当目标是近似最优动作价值函数 $Q^{\ast }$ 时，期望更新的形式为：

$$Q(s,a)\leftarrow \sum _{s^{\prime },r}\hat{p}(s^{\prime },r\mid s,a)\left[r+\gamma \underset{a^{\prime }}{\max }Q(s^{\prime },a^{\prime })\right].\text{\hspace{1em}(8.1)}$$

该公式直接体现了贝尔曼最优方程。更新过程中，对每个可能的 $(s^{\prime },r)$ 组合，以其发生概率 $\hat{p}(s^{\prime },r\mid s,a)$ 作为权重，计算折扣后的最优后续价值 ${\max }_{a^{\prime }}Q(s^{\prime },a^{\prime })$，再与即时奖励 $r$ 相加。这种方式是确定性的、精确的，但前提是模型 $\hat{p}$ 已知，因此主要用于规划场景。

采样更新

采样更新则不需要完整的环境模型。它仅依赖一次实际或模拟的经验转移 $(s,a,R,S^{\prime })$，即在状态 $s$ 执行动作 $a$ 后，观察到奖励 $R$ 和下一状态 $S^{\prime }$。基于这一单一样本，算法通过时序差分误差对价值函数进行增量调整。

针对 $Q^{\ast }$ 的采样更新（即 Q-learning 的核心规则）为：

$$Q(s,a)\leftarrow Q(s,a)+\alpha [R+\gamma \underset{a^{\prime }}{\max }Q(S^{\prime },a^{\prime })-Q(s,a)],\text{\hspace{1em}(8.2)}$$

其中 $\alpha >0$ 是步长参数，控制更新的幅度。

此更新使用采样得到的 $R$ 和 $S^{\prime }$ 构造一个对目标价值 $r+\gamma {\max }_{a^{\prime }}Q(s^{\prime },a^{\prime })$ 的随机估计。尽管单次更新带有噪声，但在适当条件下（如步长满足 Robbins-Monro 条件），多次更新的期望会收敛到最优动作价值函数。该方法不依赖模型，适用于无模型学习，是在线强化学习的典型代表。

比较

基本差异

在随机环境中，期望更新和采样更新的根本区别在于如何处理后继状态的不确定性。期望更新依赖环境模型 $\hat{p}(s^{\prime },r\mid s,a)$，对所有可能的后继状态和奖励进行加权平均，从而实现一次精确的贝尔曼备份。其误差仅来源于后继状态价值估计的不准确。采样更新则仅使用单次观测到的转移 $(s,a,R,S^{\prime })$，因此除了后继价值误差外，还会引入采样噪声。

计算代价的对比

对于一个状态-动作对 $(s,a)$，若其分支因子为 $b$（即存在 $b$ 个满足 $\hat{p}(s^{\prime }\mid s,a)>0$ 的后继状态），则完成一次期望更新所需的计算量大约是单次采样更新的 $b$ 倍。这意味着，在相同的计算预算下，执行一次期望更新所消耗的资源足以完成 $b$ 次采样更新。

精度与资源的权衡

当计算资源非常充裕且问题规模较小时，期望更新因其无采样误差的特性，通常能提供比 $b$ 次采样更新更准确的估计。然而，在大规模强化学习问题中，状态-动作对的数量极其庞大，对每个对执行高开销的期望更新往往不可行。此时，将有限的计算资源分散用于多个状态-动作对的采样更新，通常能带来更高效的全局改进。

单位计算量下的性能分析

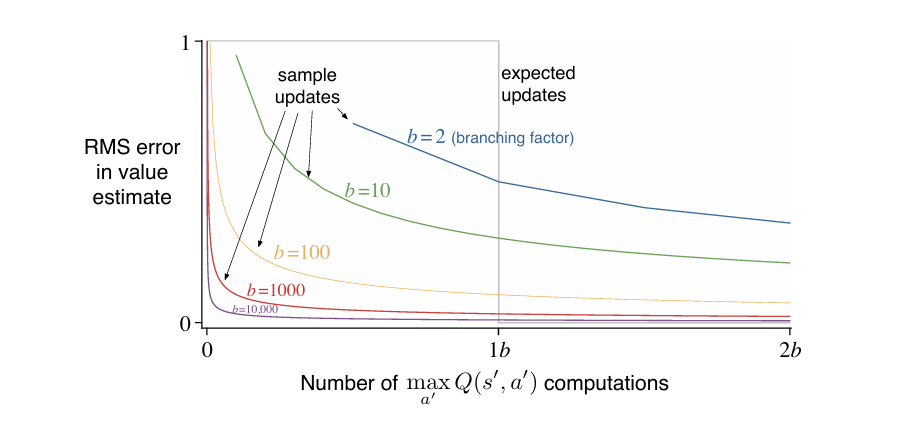
上图所示实验基于以下理想化设定：所有 $b$ 个后继状态等概率出现，后继状态的价值已准确已知，初始估计误差为 1。

横轴表示的是对后继状态动作价值取最大值的操作次数，即计算 ${\max }_{a^{\prime }}Q(s^{\prime },a^{\prime })$ 的总次数。这个指标被选为衡量计算量的核心标准，因为在期望更新中，对一个 $(s,a)$ 对进行一次完整更新，需要遍历所有 $b$ 个可能的后继状态 $s^{\prime }$，并对每个 $s^{\prime }$ 计算 ${\max }_{a^{\prime }}Q(s^{\prime },a^{\prime })$ ，因此一次期望更新对应 $b$ 次 ${\max }_{a^{\prime }}Q(s^{\prime },a^{\prime })$ 计算。在采样更新中，每次只访问一个采样到的 $S^{\prime }$，只需计算一次 ${\max }_{a^{\prime }}Q(S^{\prime },a^{\prime })$ ，因此一次采样更新对应 1 次 ${\max }_{a^{\prime }}Q(s^{\prime },a^{\prime })$ 计算。因此，横轴统一了两种更新方式的计算代价。无论是期望更新还是采样更新，都以“执行了多少次 ${\max }_{a^{\prime }}Q(s^{\prime },a^{\prime })$”作为衡量标准。这样就能公平地比较在相同计算开销下，哪种方法能更快降低误差。

纵轴是价值估计的均方根误差，用于衡量当前估计的 $Q(s,a)$ 与真实最优值 $Q^{\ast }(s,a)$ 之间的差距。初始时，误差设为 1（归一化处理），随着更新进行，误差下降，误差越低，说明价值函数估计越准确。该指标反映的是单个状态-动作对 $(s,a)$ 的估计精度。。

在此条件下，期望更新一次即可将误差降至零，而采样更新的误差随更新次数 $t$ 按比例 $\sqrt{\frac{b-1}{bt}}$ 衰减（采用平均步长 $\alpha =1/t$）。

尽管期望更新在单个状态-动作对上更精确，但其高计算成本限制了其覆盖范围。相同计算量下，采样更新可作用于多个不同的状态-动作对。上图显示，对于中等大小的分支因子 $b$，仅需少量采样更新即可显著降低整体估计误差。这种广撒网式的更新策略在整体价值函数收敛速度上更具优势。

**综合来看，在具有较大随机分支因子且需要处理大量状态-动作对的实际问题中，采样更新在单位计算量下的效率通常优于期望更新。**其低计算开销、良好的可扩展性，以及对价值改进的快速传播能力，使其成为大规模强化学习系统中的更优选择。