高阶数据结构 --- Trie 树

大家好，我们又见面了。这一期，我来给大家介绍一个高阶数据结构：Trie 树。

字典树在计算机领域还是非常常见的，相信这篇文章一定会对大家有所帮助。

创作不易！！！别忘了一键三连~~~

废话不多说，我们直接开启这一期的内容。

一：字典树的概念

Trie 树又叫字典树或前缀树，是一种能够快速处理插入和查询字符串的数据结构。它利用字符串的公共前缀，将字符串组织成一颗树形结构，从而大大提高了存储以及查询的效率。

注：哈希表和红黑树也可以做到快速处理插入和查询字符串的操作。但这并不能说明字典树的设计是多余的，字典树可以做到一些它们做不到的事情。

我们可以把字典树想象成为一颗多叉树，其中每一条边代表一个字符，从根节点到某个节点的路径就代表了一个字符串。例如，要存储 "abc" "abd" "acde" 以及 "cd" 时，构建的字典树如下：

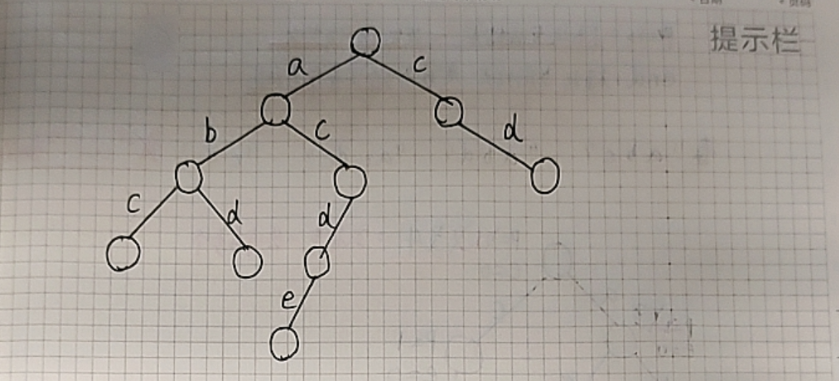
上述字典树构建过程：（自己多模拟几遍）

1. 一个字符串一个字符串遍历，当遍历到某一个字符串时，遍历它的每一个字符。

2. 第一个字符对应树的第一二层之间的边，第二个字符对应树的第二三层之间的边，依次类推。

3. 初始状态下，字典树只有一个根节点（第一层）。

2. 从根节点开始，如果有对应这一个字符的路径，就复用，走下去，如果没有，就创建路径。

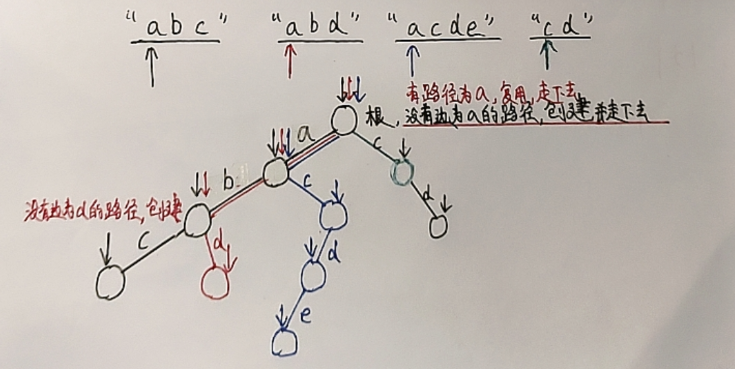
这样创建完毕之后，处理查询字符串的逻辑也与插入字符串类似。一层一层往下走。

比如：查询字符串 "acde" "ad" ，一层一层往下走，发现 "acde" 存在，"ad" 并不存在。

自己下去模拟，详细过程这里不赘述了。

但是按照上面方式创建出的字典树是有一定问题的。比如：

1. 我们我们想要查询字符串 "ac" 是否存在，按照上述方式是会判断它存在的，但是实际并没有插入 "ac" 字符串。

2. 再比如，如果我们之前插入了 "acde"，现在又要插入 "ac"，这时实际就存在 "ac" 字符串了。

3. 再比如，如果我们插入了很多个 "ac" 字符串，查询的时候怎么才能知道插入了多少个呢？？？

基于上述问题，我们在字典树的每一个结点上多维护两个变量：

1. pass：标记当前结点一共出现 / 经过了多少次。

2. end：标记当前结点是以多少个字符串为结尾。

然后我们在插入字符串的同时维护好每一个节点的信息，就可以解决上面的问题了。

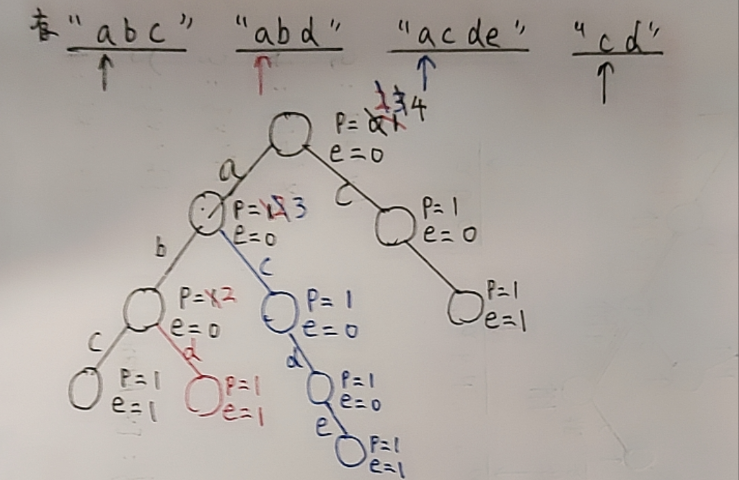
这样的话，就很好的解决了上面的问题。

二：字典树的作用

当我们在字典树的每一个节点位置，额外维护一些信息时，就可以做到很多事情：

1. 查询某一个单词是否出现过，并且出现过几次。

2. 查询有多少个单词是以某一个字符串为前缀。

3. 查询所有以某个前缀开头的单词。（dfs 子树）

三：字典树的模拟实现

我们实现一个能够查询某单词出现次数以及查询有多少个单词是以某个字符串为前缀的字典树。

默认全是小写字母 a~z：

1. 准备工作

#include <iostream>
#include <cstring>using namespace std;
const int N = 1e6 + 10;int tree[N][26], p[N], e[N];
int idx;

N：表示所有的字符串中一共出现了多少个字符。（字典树的节点个数最差情况都不复用）

tree[i]：表示 i 号结点的孩子信息

tree[i][0]：表示 'a' 的路径信息

tree[i][1]：表示 'b' 的路径信息

tree[i][2]：表示 'c' 的路径信息

…………

p[i]：表示 i 号结点的 pass 信息

e[i]：表示 i 号结点的 end 信息

idx：新来一个字符之后，为它分配位置。

接下来通过一张图深刻理解一下 tree 数组的作用：

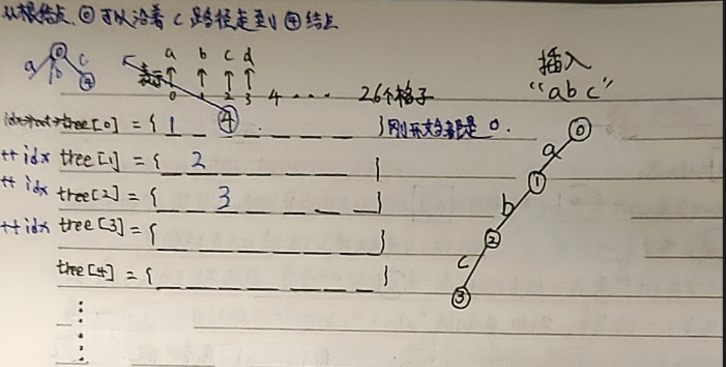
2. 插入字符串

void insert(string& s)
{int cur = 0; // 从根节点开始考虑p[cur]++;    // 这个格子经过一次for (auto ch : s){int path = ch - 'a'; // 对应路径编号// 如果没有路,自己开辟一条路if (tree[cur][path] == 0) tree[cur][path] = ++idx;cur = tree[cur][path]; // 走下去p[cur]++; // 维护节点的 pass 信息}e[cur]++; // 最后别忘了维护 e 信息
}

3. 查询字符串出现的次数

int find(string& s)
{int cur = 0; // 从根节点开始for (auto ch : s){int path = ch - '0'; // 路径编号if (tree[cur][path] == 0) return 0; // 没有路，找不到cur = tree[cur][path]; // 走下去}return e[cur]; // 找到了，返回出现的次数
}

4. 查询有多少个单词以字符串 s 为前缀

int find_pre(string& s)
{int cur = 0;for (auto ch : s){int path = ch - '0';if (tree[cur][path] == 0) return 0;cur = tree[cur][path];}return p[cur];
}

建议：一定要下去之后自己多找几个字符串模拟几遍，只要明白了原理，代码是很简单的。

好的，这一期的分享就到这里了，我们下一期再见。