LeetCode算法日记 - Day 73: 最小路径和、地下城游戏

目录

1. 最小路径和

1.1 题目解析

1.2 解法

1.3 代码实现

2. 地下城游戏

2.1 题目解析

2.2 解法

2.3 代码实现

---

1. 最小路径和

https://leetcode.cn/problems/minimum-path-sum/description/

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

示例 1：

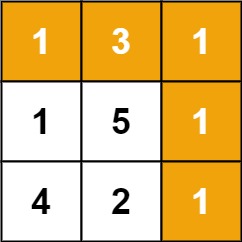
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

示例 2：

输入：grid = [[1,2,3],[4,5,6]]
输出：12

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 200
• 0 <= grid[i][j] <= 200

1.1 题目解析

题目本质
这是"选择最小值"问题，不是"加最小值"问题。对比下降路径最小和，那道题第一行的三个方向都来自 dp[0][]，全是 0，加起来还是当前格子值，不影响结果。但最小路径和的第一行会从左边累加（dp[1][1] → dp[1][2] → dp[1][3]），如果 dp[0][j] = 0，会被 Math.min 错误选中

常规解法
最直观的想法是用递归/DFS枚举所有路径：从起点开始，每个位置尝试向右和向下两个方向，递归到终点时记录路径和，最后取最小值。

问题分析
纯递归会超时。对于 200×200 的网格，最坏情况时间复杂度接近 O(2^400)，且存在大量重复计算。比如计算到达 (10,10) 的最小路径和会被多次重复计算。

思路转折
要想高效 → 必须消除重复计算 → 使用动态规划。
关键观察：到达某个格子 (i,j) 的最小路径和 = 当前格子的值 + min(从左边来的最小路径和, 从上边来的最小路径和)。注意这里是"选择"左边或上边中更小的那个，而不是"累加"。通过自底向上填表，每个状态只计算一次。

1.2 解法

算法思想

使用二维 DP，定义 dp[i][j] 表示从起点到达位置 (i,j) 的最小路径和。

递推公式：

dp[i][j] = grid[i-1][j-1] + min(dp[i-1][j], dp[i][j-1])

边界条件：

• dp[1][1] = grid[0][0]（起点）

• 第 0 行和第 0 列初始化为 MAX_VALUE（不可达）

i）创建 (m+1) × (n+1) 的 dp 数组，使用 1-索引

ii）关键：将整个 dp 数组初始化为 Integer.MAX_VALUE

iii）单独初始化起点 dp[1][1] = grid[0][0]

iv）双层循环遍历所有格子，按递推公式取最小值

v）返回 dp[m][n] 作为答案

易错点

• 索引映射混淆：dp 数组用 1-索引，原数组用 0-索引。访问原数组时要用 grid[i-1][j-1]

• 起点处理：必须跳过起点单独赋值，否则会尝试从"上边"或"左边"取值，导致错误

1.3 代码实现

static class Solution {int[][] dp;public int minPathSum(int[][] grid) {int m = grid.length, n = grid[0].length;dp = new int[m + 1][n + 1];// 核心：全部初始化为无穷大// 原因：这是"选择最小值"问题，0 会被 Math.min 错误选中for (int i = 0; i <= m; i++) {for (int j = 0; j <= n; j++) {dp[i][j] = Integer.MAX_VALUE;}}for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {if (i == 1 && j == 1) {dp[i][j] = grid[0][0];  // 起点直接赋值continue;}// 当前最小路径和 = 当前格子 + min(上边来, 左边来)dp[i][j] = grid[i - 1][j - 1] + Math.min(dp[i][j - 1], dp[i - 1][j]);}}return dp[m][n];}
}

复杂度分析

• 时间复杂度：O(m × n)，需要遍历整个网格一次

• 空间复杂度：O(m × n)，使用了二维 dp 数组

2. 地下城游戏

https://leetcode.cn/problems/dungeon-game/description/

恶魔们抓住了公主并将她关在了地下城 dungeon 的 右下角 。地下城是由 m x n 个房间组成的二维网格。我们英勇的骑士最初被安置在 左上角 的房间里，他必须穿过地下城并通过对抗恶魔来拯救公主。

骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下，他会立即死亡。

有些房间由恶魔守卫，因此骑士在进入这些房间时会失去健康点数（若房间里的值为负整数，则表示骑士将损失健康点数）；其他房间要么是空的（房间里的值为 0），要么包含增加骑士健康点数的魔法球（若房间里的值为正整数，则表示骑士将增加健康点数）。

为了尽快解救公主，骑士决定每次只 向右 或 向下 移动一步。

返回确保骑士能够拯救到公主所需的最低初始健康点数。

注意：任何房间都可能对骑士的健康点数造成威胁，也可能增加骑士的健康点数，包括骑士进入的左上角房间以及公主被监禁的右下角房间。

示例 1：

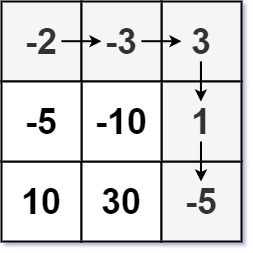
输入：dungeon = [[-2,-3,3],[-5,-10,1],[10,30,-5]]
输出：7
解释：如果骑士遵循最佳路径：右 -> 右 -> 下 -> 下 ，则骑士的初始健康点数至少为 7 。

示例 2：

输入：dungeon = [[0]]
输出：1

提示：

• m == dungeon.length
• n == dungeon[i].length
• 1 <= m, n <= 200
• -1000 <= dungeon[i][j] <= 1000

2.1 题目解析

题目本质
骑士从左上角到右下角救公主，每个房间会增减血量，关键是任何时刻血量都不能 ≤ 0。目标是求初始最少需要多少血才能保证全程存活，不同于普通的路径和问题。

常规解法
最直观的想法是正向 DP：定义 dp[i][j] 表示到达 (i,j) 时的最大剩余血量，然后选择剩余血量最大的路径，最后倒推初始需要多少血。

问题分析
正向 DP 无法解决这道题。
你在中间没法判断：

• 不知道"现在血多"是因为"起点带得多"还是"一路加得多"

• 不知道"后面需要多少血"才能不死

思路转折
从终点倒推：下一步要X血，这里加/扣Y血，那我现在要max(1, X-Y)血，推到起点就是答案。

2.2 解法

用二维 DP 从右下往左上逆向推导，定义 dp[i][j] 表示从位置 (i,j) 出发到达终点所需的最少血量。

递推公式：

next = min(dp[i+1][j], dp[i][j+1])  // 选择右边或下边需求更少的路径dp[i][j] = max(1, next - dungeon[i][j])

边界条件：

• 数组大小：(m+2) × (n+2)，为右边和下边留出边界

• 边界初始化为 MAX_VALUE（不可达）

• 终点的右边和下边设为 1：dp[m][n+1] = dp[m+1][n] = 1

i）创建 (m+2) × (n+2) 的 dp 数组，使用 1-索引，多留一行一列给右边和下边

ii）将整个 dp 数组初始化为 Integer.MAX_VALUE（表示不可达）

iii）设置虚拟边界：dp[m][n+1] = 1 和 dp[m+1][n] = 1，表示"通关后"至少要 1 点血

iv）从右下往左上遍历：外层循环 i 从 m 到 1，内层循环 j 从 n 到 1

v）每个位置取右边和下边的最小需求，倒推当前位置的需求

vi）返回 dp[1][1]（起点需要的血量）

易错点

• DP 方向错误：这道题必须从右下往左上推，正向 DP 无法得到正确答案。循环必须是 i = m → 1 和 j = n → 1

• 边界设置方向错误：要设置终点的右边 dp[m][n+1] 和下边 dp[m+1][n]，不是左边或上边。因为逆向推导时，终点会访问 dp[i][j+1] 和 dp[i+1][j]

• 数组大小不够：必须开 [m+2][n+2]，不能是 [m+1][n+1]，否则访问 dp[m][n+1] 和 dp[m+1][n] 会越界

• 忘记 max(1, ...)：即使当前房间加血很多（如 +100），理论计算可能得到 ≤0 的值，但必须保证进入任何房间前至少 1 点血。公式中的 max(1, ...) 不能省略

• 减法的理解：next - dungeon[i][j] 中，如果当前房间是正数（加血），需求会减少；如果是负数（扣血），需求会增加。当 next - dungeon[i][j] ≤ 0 时，说明当前房间加的血 ≥ 后面需要的血，带 1 点血进入就够了

2.3 代码实现

static class Solution {// 核心逻辑：你当前格子是 Y，下一个格子需要 X 点血// 那你进入当前格子前需要：max(1, X - Y)int[][] dp;public int calculateMinimumHP(int[][] num) {int m = num.length, n = num[0].length;dp = new int[m + 2][n + 2];  // 多开一行一列给右边和下边// 边界初始化为无穷大（不可达区域）for (int i = 0; i <= m + 1; i++) {for (int j = 0; j <= n + 1; j++) {dp[i][j] = Integer.MAX_VALUE;}}// 终点的右边和下边设为 1// 意思：通关后的"虚拟下一步"需要 1 点血（保证终点计算正确）dp[m][n + 1] = 1;dp[m + 1][n] = 1;// 从右下往左上推导for (int i = m; i >= 1; i--) {for (int j = n; j >= 1; j--) {// 下一步需求：选择右边或下边需求更少的int next = Math.min(dp[i][j + 1], dp[i + 1][j]);// 当前需求 = max(1, 下一步需求 - 当前房间值)dp[i][j] = Math.max(1, next - num[i - 1][j - 1]); }}return dp[1][1];  // 起点需要的血量}
}

复杂度分析

• 时间复杂度：O(m × n)，需要遍历整个网格一次

• 空间复杂度：O(m × n)，使用了二维 dp 数组