算法训练之BFS解决最短路径问题

♥♥♥~~~~~~欢迎光临知星小度博客空间~~~~~~♥♥♥
♥♥♥零星地变得优秀~也能拼凑出星河~♥♥♥
♥♥♥我们一起努力成为更好的自己~♥♥♥
♥♥♥如果这一篇博客对你有帮助~别忘了点赞分享哦~♥♥♥
♥♥♥如果有什么问题可以评论区留言或者私信我哦~♥♥♥
✨✨✨✨✨✨ 个人主页✨✨✨✨✨✨
这一篇博客我们继续来应用BFS算法解决一些具体问题,准备好了吗~我们发车去探索BFS的奥秘啦~🚗🚗🚗🚗🚗🚗
目录
迷宫中离入口最近的出口😁
最小基因变化😊
单词接龙😝
为高尔夫比赛砍树🙃
迷宫中离入口最近的出口😁
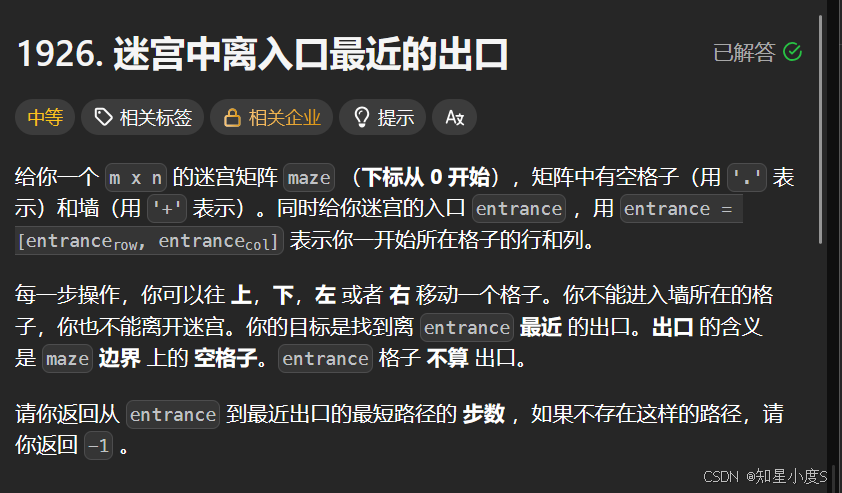
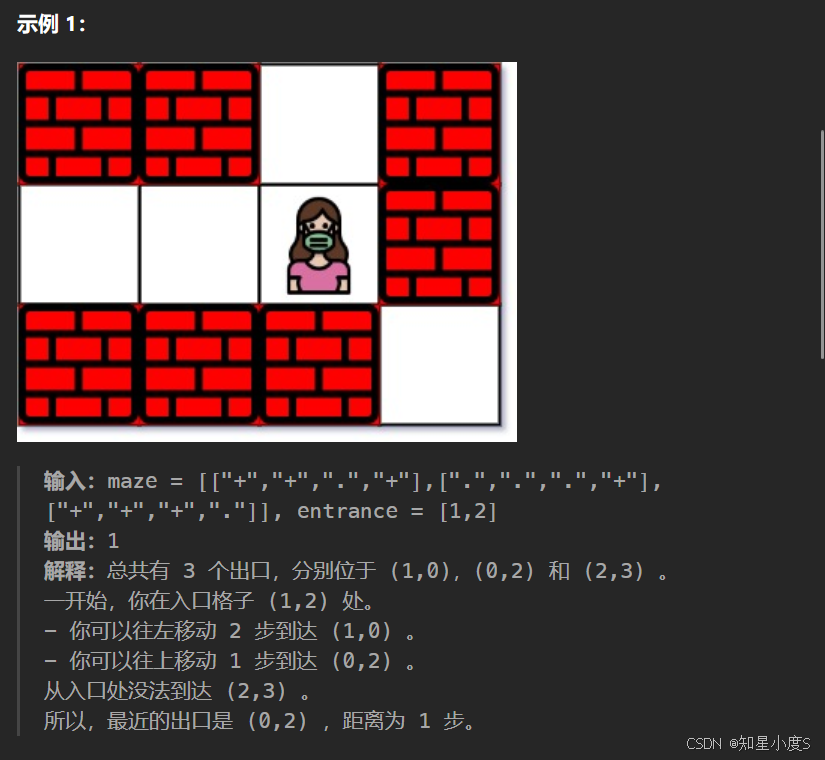
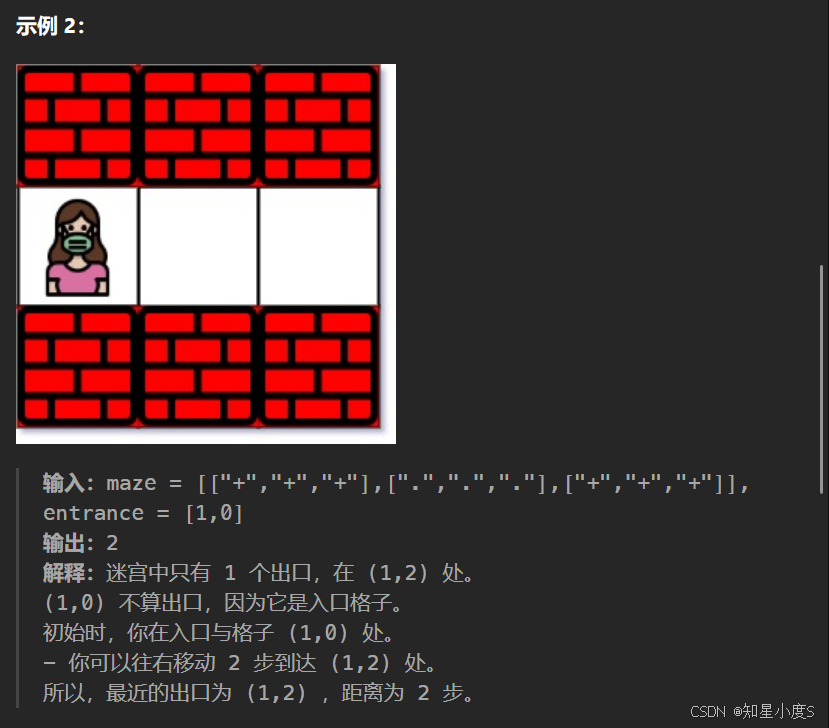
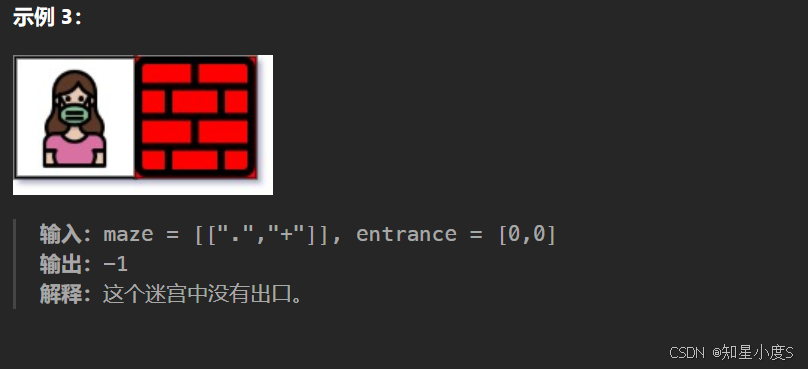
迷宫中离入口最近的出口
🧠 算法思路:
①BFS 初始化:从入口开始,步数初始为 0
②逐层扩展:每次处理一层的所有节点,步数 +1
③判断出口:
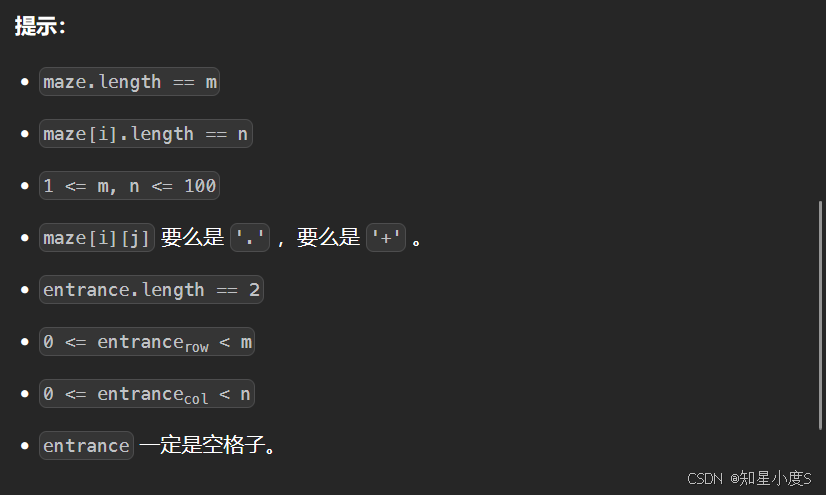
出口是边界上的空格子(maze[cx][cy] == '.')
出口不能是入口
④剪枝:
遇到墙('+')跳过,已访问的格子不再处理~
⑤结果:
找到出口 → 返回当前步数
队列为空仍未找到 → 返回 -1
代码实现:
//迷宫中离入口最近的出口
class Solution
{typedef pair<int, int> PII;//方便写类型//方便遍历某一个位置上下左右四个方向int dx[4] = { 0,0,-1,1 };int dy[4] = { -1,1,0,0 };bool vis[101][101];//记录是否被访问int m = 0, n = 0;//记录行列
public:int nearestExit(vector<vector<char>>& maze, vector<int>& entrance){//获取行列m = maze.size();n = maze[0].size();queue<PII> q;//队列保存位置q.push({ entrance[0],entrance[1] });//入口入队列标记为被访问,不会成为出口vis[entrance[0]][entrance[1]] = true;int step = 0;//记录步数while (q.size()){step++;int sz = q.size();//处理当前层for (int i = 0; i < sz; i++){auto [qx, qy] = q.front();q.pop();for (int k = 0; k < 4; k++){int cx = qx + dx[k], cy = qy + dy[k];if (cx >= 0 && cx < m && cy >= 0 && cy < n && maze[cx][cy] == '.' && !vis[cx][cy]){//到达边界,返回步数if (cx == 0 || cx == m - 1 || cy == 0 || cy == n - 1){return step;}q.push({ cx,cy });vis[cx][cy] = true;}}}}//不存在路径,返回-1return -1;}
};
顺利通过~
最小基因变化😊
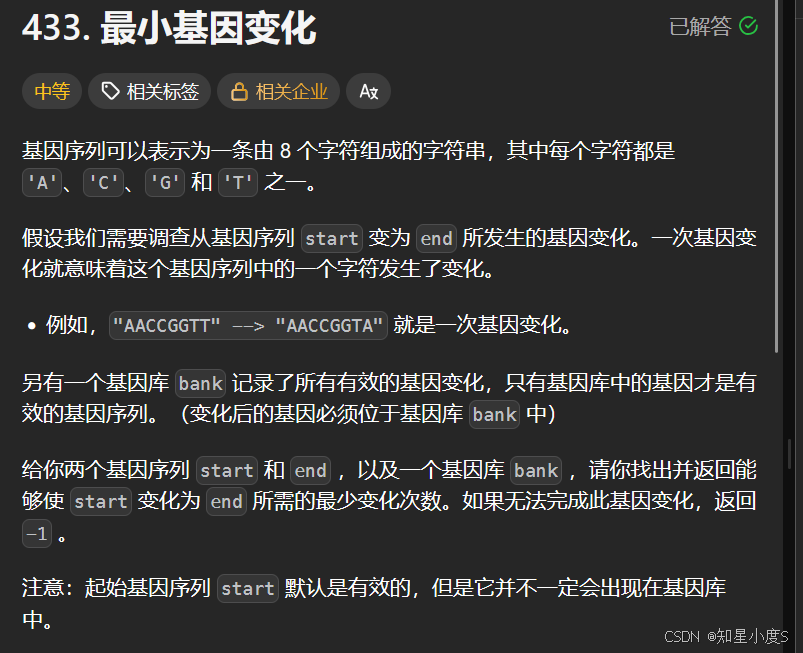
最小基因变化
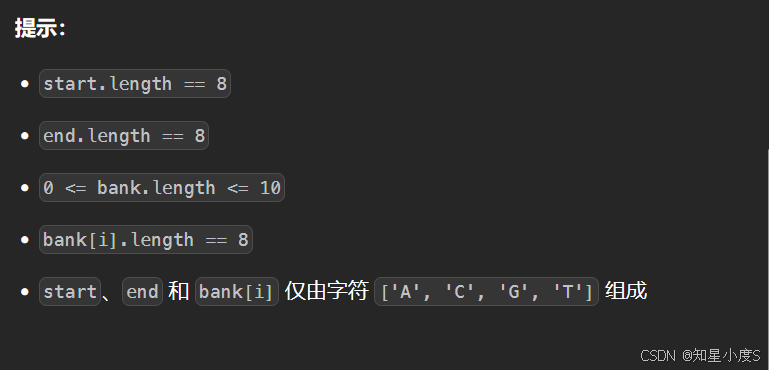
🧠算法思路:
1. 预处理与边界检查
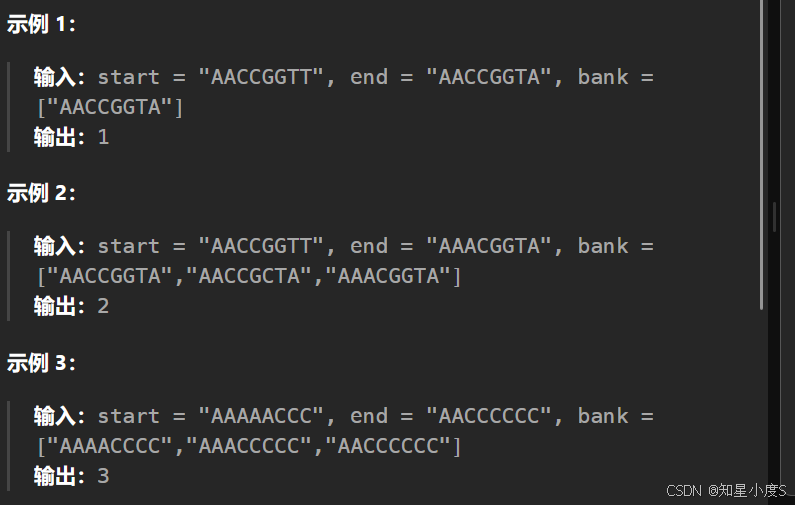
检查起始基因是否等于目标基因(直接返回0)
验证目标基因是否存在于基因库中(不存在则返回-1)
将基因库转换为哈希集合以提高查找效率
2. BFS初始化
创建队列并将起始基因加入队列
建立已访问集合,记录已处理过的基因序列
初始化步数计数器为0
3. 层序遍历策略
按层处理队列中的基因序列
每处理完一层,步数增加1
确保找到的路径是最短路径
4. 基因变化生成
对当前基因序列的每个位置(共8个)
尝试替换为其他三种可能的碱基(A/C/G/T)
生成所有可能的单次突变结果
5. 有效性验证
检查新生成的基因是否在基因库中
验证该基因是否已被访问过
避免重复处理相同状态
6. 目标检测
比较新生成的基因与目标基因
若匹配则立即返回当前步数
否则加入队列继续搜索
7. 终止条件
成功找到目标基因 → 返回变化次数
队列耗尽仍未找到 → 返回-1(无解)
代码实现:
//最小基因变化
class Solution
{
public:int minMutation(string startGene, string endGene, vector<string>& bank){//记录已经生成的字符串unordered_set<string> vis;//使用unordered_set保存基因库,方便查找unordered_set<string> ban(bank.begin(), bank.end());//处理边界特殊情况if (startGene == endGene)return 0;if (!ban.count(endGene))return -1;//变化字符string change = "AGCT";//记录变化次数int step = 0;queue<string> q;q.push(startGene);vis.insert(startGene);while (q.size()){int sz = q.size();step++;while (sz--){string qs = q.front();q.pop();//逐个修改当前字符串每一个字符for (int i = 0; i < 8; i++){string tmp = qs;for (int k = 0; k < 4; k++){tmp[i] = change[k];//没有被访问并且在基因库中if (!vis.count(tmp) && ban.count(tmp)){if (tmp == endGene)return step;q.push(tmp);vis.insert(tmp);}}}}}//没有结果,返回-1return -1;}
};
顺利通过~
单词接龙😝
单词接龙
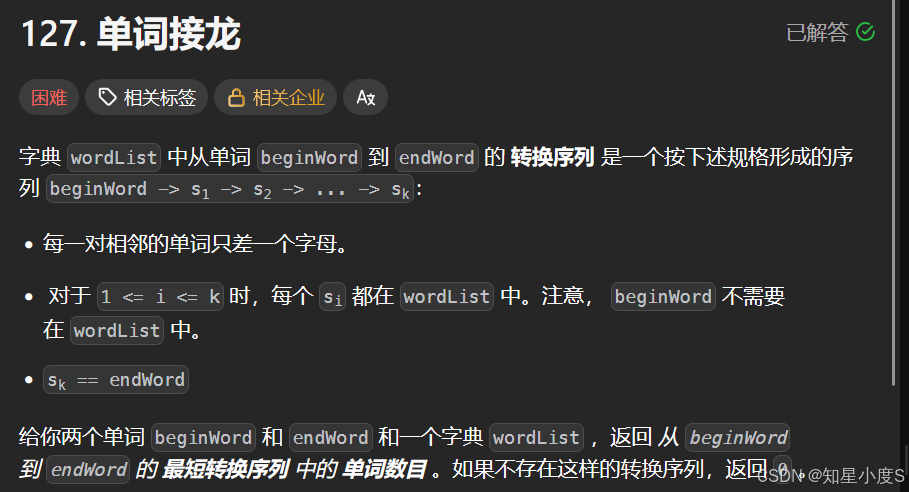

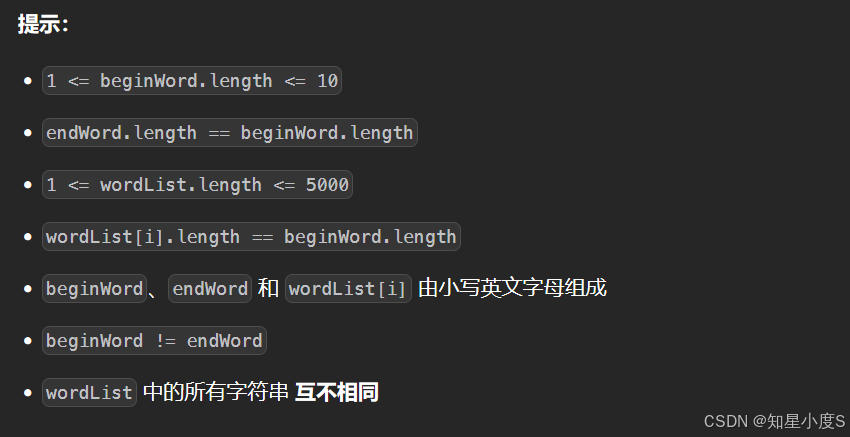
这一个题目与前面一个题目是类似的,我们一样首先来看看算法思路~
🧠算法思路:
1. 数据预处理
将 wordList 转换为哈希集合,实现O(1)时间复杂度的查找
创建已访问集合,避免重复处理相同单词
2. 边界条件检查
检查 endWord 是否在单词列表中(不在则直接返回0)
题目提示 beginWord ≠ endWord,可选择性处理相等情况
3. BFS初始化
初始化步数计数器为1(包含起始单词)
将 beginWord 加入队列和已访问集合
4. 分层遍历策略
按层处理队列中的单词
每处理完一层,步数增加1
确保找到的路径是最短的
5. 单词变换生成
对当前单词的每个位置
尝试替换为26个小写字母中的每一个
生成所有可能的单字母差异单词
6. 有效性验证
检查新单词是否在单词列表中
验证该单词是否已被访问过
7. 目标检测与终止
如果新单词等于 endWord,立即返回当前步数
否则将有效新单词加入队列继续搜索
代码实现:
//单词接龙
class Solution
{
public:int ladderLength(string beginWord, string endWord, vector<string>& wordList){//记录是否被访问unordered_set<string> vis;//记录字典中的单词unordered_set<string> words(wordList.begin(), wordList.end());//处理边界特殊情况if (beginWord == endWord)return 0;//这种特殊情况可以不处理,题目提示beginWord!=endWordif (!words.count(endWord))return 0;//记录变化字符串个数int step = 0;//获取字符串长度int sn = beginWord.size();//队列进行BFS遍历保存queue<string> q;q.push(beginWord);vis.insert(beginWord);step++;//第一个字符串也进行计数while (q.size()){step++;//字符串个数++int sz = q.size();while (sz--){string qs = q.front();q.pop();//依次修改当前字符串的每一个字符for (int i = 0; i < sn; i++){string tmp = qs;for (char c = 'a'; c <= 'z'; c++){tmp[i] = c;if (!vis.count(tmp) && words.count(tmp)){if (tmp == endWord)return step;q.push(tmp);vis.insert(tmp);}}}}}//没有结果,返回0return 0;}
};
顺利通过~
为高尔夫比赛砍树🙃
为高尔夫比赛砍树

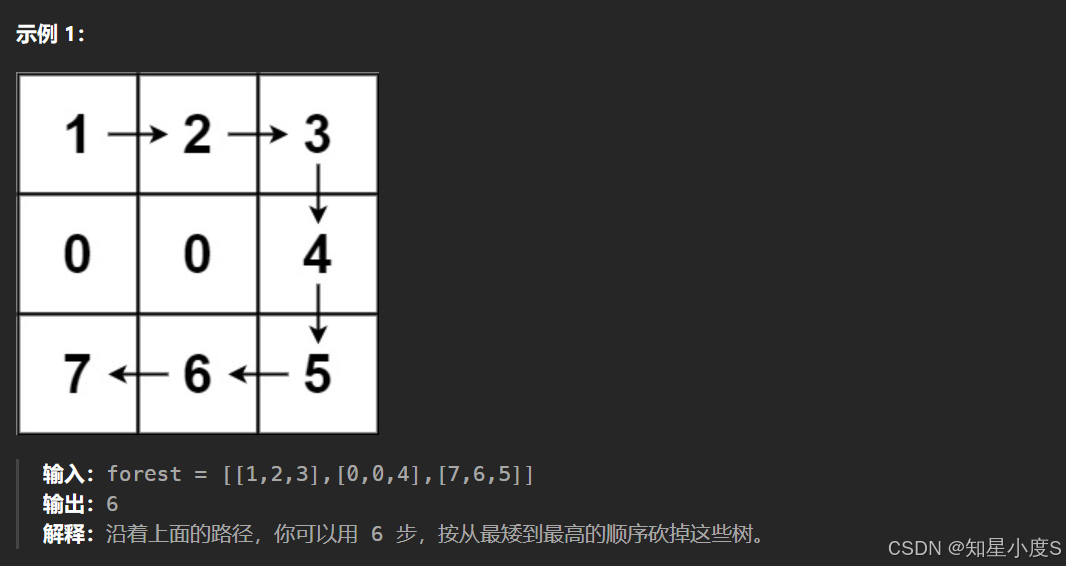


🧠算法思路:
1. 数据预处理
收集所有树的位置:遍历整个网格,记录所有高度大于1的树的位置
按高度排序:根据树的高度值对位置进行升序排序,确定砍树顺序
2. 路径计算
起点初始化:从(0,0)位置开始
顺序访问树木:按照排序后的顺序依次访问每棵树
累计步数:计算从当前位置到下一棵树的最短路径,并累加步数
BFS执行步骤
初始化:
重置访问标记数组
起点入队并标记为已访问
步数计数器初始化为0
分层遍历:
每次处理一层的所有节点
每进入新的一层,步数增加1
使用sz变量控制当前层节点数量
邻居扩展:
对每个节点的四个方向进行探索
检查边界条件、障碍物和访问状态
发现目标立即返回当前步数
终止条件:
找到目标位置 → 返回步数
队列为空未找到 → 返回-1
3. 异常处理
可达性检查:如果任何一棵树无法到达,立即返回-1
起点终点相同:特殊处理,步数为0
代码实现:
//为高尔夫比赛砍树
class Solution
{//方便写类型typedef pair<int, int> PII;//方便访问某一个位置上下左右四个方向int dx[4] = { 0,0,1,-1 };int dy[4] = { -1,1,0,0 };//记录行列int m = 0, n = 0;
public:int cutOffTree(vector<vector<int>>& forest){//获取行列m = forest.size();n = forest[0].size();//1、按照树的高度进行排序vector<PII> trees;for (int i = 0; i < m; i++){for (int j = 0; j < n; j++){if (forest[i][j] > 1){trees.push_back({ i,j });}}}//根据高度对位置进行排序sort(trees.begin(), trees.end(), [&](const PII& p1, const PII& p2) {return forest[p1.first][p1.second] < forest[p2.first][p2.second];});//2、根据排序顺序依次找到最短路径int step = 0;//记录步数int bx = 0, by = 0;//起点【0,0】for (auto& [ex, ey] : trees){int ret = bfs(forest, bx, by, ex, ey);//无法到达,不存在路径if (ret == -1)return -1;//可以到达累积步数step += ret;//更新起点bx = ex, by = ey;}//3、返回结果return step;}//记录是否被访问bool vis[51][51] = { false };//BFS计算两个位置最短路径int bfs(vector<vector<int>>& forest, int bx, int by, int ex, int ey){//处理边界特殊情况——起点就是指定位置if (bx == ex && by == ey)return 0;memset(vis, 0, sizeof vis);//清除之前的记录queue<PII> q;q.push({ bx,by });vis[bx][by] = true;int ret = 0;//记录最小步数while (q.size()){ret++;int sz = q.size();while (sz--){auto [qx, qy] = q.front();q.pop();for (int i = 0; i < 4; i++){int cx = qx + dx[i], cy = qy + dy[i];if (cx >= 0 && cx < m && cy >= 0 && cy < n && !vis[cx][cy] && forest[cx][cy])//不越界,不是墙,未被访问——三者同时满足{//到达指定位置(下一个位置)返回步数if (cx == ex && cy == ey)return ret;//否则入队列,标记被访问,继续后续操作q.push({ cx,cy });vis[cx][cy] = true;}}}}//不能到达指定位置,返回-1return -1;}
};
顺利通过~
♥♥♥本篇博客内容结束,期待与各位优秀程序员交流,有什么问题请私信♥♥♥
♥♥♥如果这一篇博客对你有帮助~别忘了点赞分享哦~♥♥♥
✨✨✨✨✨✨个人主页✨✨✨✨✨✨
