当前位置： 首页 > news >正文

卷积值提取

news 2025/10/17 8:03:12

【1】引言

前序学习进程中，初步了解了CNN卷积计算组件，点击链接直达：

https://blog.csdn.net/weixin_44855046/article/details/152836857

实践出真知，今天就更进一步，尝试改一改代码。

改之前，先给出上一篇文章中的完整代码：

# 引入模块
# 为了实现计算过程详细展示，只使用了数学计算模块numpy和画图模块matplotlib
import numpy as np
import matplotlib.pyplot as plt# --------------------------
# 1. 定义输入和卷积核（简化尺寸便于观察）
# --------------------------
# 输入图像：4x4的简单矩阵（模拟灰度图）
input_image = np.array([[1, 2, 3, 0],[4, 5, 6, 0],[7, 8, 9, 0],[0, 0, 0, 0]
], dtype=np.float32)
# 先输出一下原始图像
plt.imshow(input_image, cmap='gray', vmin=0, vmax=9)
# 卷积核：2x2（用于提取简单特征）
kernel = np.array([[1, 0],[0, -1]
], dtype=np.float32)# 步长手动设置，可以改变
stride = 1  # 步长为1# --------------------------
# 2. 手动计算卷积过程并记录每一步
# --------------------------
# 用input_h, input_w分别提取原始图像input_image的高度和长度
input_h, input_w = input_image.shape
# 用kernel_h, kernel_w分别提取卷积核kernel的高度和长度
kernel_h, kernel_w = kernel.shape
# 先计算差分，可以知道原始矩阵和卷积核的大小差多少
# 实际上差多少，卷积核就要滑动多少步
# 但在最开始的时候，卷积核天然的就可以覆盖原始矩阵的一部分，因为覆盖，所以差分=0
# 所以这一步已经存在了，所以实际的步骤还要+1
out_h = (input_h - kernel_h) // stride + 1  # 输出高度：3
out_w = (input_w - kernel_w) // stride + 1  # 输出宽度：3# 存储每一步的滑动窗口和计算结果
steps = []  # 每个元素是 (窗口区域, 计算过程字符串, 结果值)# 卷积计算过程
for i in range(out_h):for j in range(out_w):# 提取当前滑动窗口（输入的局部区域）start_i, start_j = i * stride, j * stride# 因为+ kernel_h和+ kernel_w，实现真正的滑动# 这里实际上将每一小块元素都单独取出来了，就是windowswindow = input_image[start_i:start_i + kernel_h, start_j:start_j + kernel_w]# 计算卷积：元素相乘再求和product = window * kernel  # 元素相乘result = np.sum(product)  # 求和# 记录计算过程（用于可视化）# 由于取出来的windows大小都是2行2列，所以实现计算的过程中只需要关注[0,0],[0,1],[1,0]和[1,1]这四个位置# 先算第一行calc_str = f"({window[0, 0]}×{kernel[0, 0]}) + ({window[0, 1]}×{kernel[0, 1]}) + \n"# 再算第二行calc_str += f"({window[1, 0]}×{kernel[1, 0]}) + ({window[1, 1]}×{kernel[1, 1]}) = \n"# 将前两步计算获得的结果相加calc_str += f"({product[0, 0]}) + ({product[0, 1]}) + ({product[1, 0]}) + ({product[1, 1]}) = {result}"# 保存所有元素steps.append((window, calc_str, result))# --------------------------
# 3. 可视化卷积全过程（修正子图布局为4x3）
# --------------------------
plt.figure(figsize=(15, 12))  # 增大画布尺寸# 显示输入图像和卷积核
plt.subplot(4, 3, 1)  # 第1个位置
plt.title("input_image (4x4)")
plt.imshow(input_image, cmap='gray', vmin=0, vmax=9)
for i in range(input_h):for j in range(input_w):plt.text(j, i, f"{input_image[i, j]}", ha='center', va='center', color='red')plt.subplot(4, 3, 2)  # 第2个位置
plt.title("CNN_kernel (2x2)")
plt.imshow(kernel, cmap='gray', vmin=-1, vmax=1)
for i in range(kernel_h):for j in range(kernel_w):plt.text(j, i, f"{kernel[i, j]}", ha='center', va='center', color='blue')# 显示输出特征图（3x3）
feature_map = np.array([s[2] for s in steps]).reshape(out_h, out_w)
plt.subplot(4, 3, 3)  # 第3个位置
plt.title("output_image (3x3)")
plt.imshow(feature_map, cmap='gray')
for i in range(out_h):for j in range(out_w):plt.text(j, i, f"{feature_map[i, j]:.0f}", ha='center', va='center', color='green')# 显示每一步的滑动窗口和计算过程（共9步，从第4个位置开始）
for idx, (window, calc_str, result) in enumerate(steps, start=4):plt.subplot(4, 3, idx)  # 4x3网格支持到第12个位置，足够容纳9步plt.title(f"steps{idx - 3}:location ({(idx - 4) // 3}, {(idx - 4) % 3})")plt.imshow(window, cmap='gray', vmin=0, vmax=9)for i in range(kernel_h):for j in range(kernel_w):plt.text(j, i, f"{window[i, j]}", ha='center', va='center', color='red')plt.text(1.5, 0.5, calc_str, ha='left', va='center', fontsize=8, color='purple')plt.tight_layout()
plt.show()

【2】卷积值

尝试输出卷积值是一个好的方法，可以辅助我们理解卷积究竟卷了啥。

这一步非常简单，在基础型代码中，为了展示过程，我们其实重复定义了计算过程：

for i in range(out_h):for j in range(out_w):# 提取当前滑动窗口（输入的局部区域）start_i, start_j = i * stride, j * stride# 因为+ kernel_h和+ kernel_w，实现真正的滑动# 这里实际上将每一小块元素都单独取出来了，就是windowswindow = input_image[start_i:start_i + kernel_h, start_j:start_j + kernel_w]# 计算卷积：元素相乘再求和product = window * kernel  # 元素相乘result = np.sum(product)  # 求和

这是第一部分的计算，非常的简洁高效。

然后为了展示每一次卷积计算，又换了一种方式写代码：

# 卷积计算过程
for i in range(out_h):for j in range(out_w):# 提取当前滑动窗口（输入的局部区域）start_i, start_j = i * stride, j * stride# 因为+ kernel_h和+ kernel_w，实现真正的滑动# 这里实际上将每一小块元素都单独取出来了，就是windowswindow = input_image[start_i:start_i + kernel_h, start_j:start_j + kernel_w]# 计算卷积：元素相乘再求和product = window * kernel  # 元素相乘result = np.sum(product)  # 求和        # 记录计算过程（用于可视化）# 由于取出来的windows大小都是2行2列，所以实现计算的过程中只需要关注[0,0],[0,1],[1,0]和[1,1]这四个位置# 先算第一行calc_str = f"({window[0, 0]}×{kernel[0, 0]}) + ({window[0, 1]}×{kernel[0, 1]}) + \n"# 再算第二行calc_str += f"({window[1, 0]}×{kernel[1, 0]}) + ({window[1, 1]}×{kernel[1, 1]}) = \n"# 将前两步计算获得的结果相加calc_str += f"({product[0, 0]}) + ({product[0, 1]}) + ({product[1, 0]}) + ({product[1, 1]}) = {result}"# 保存所有元素steps.append((window, calc_str, result))

我们现在就对这两种计算都提取一下计算结果。

由于steps已经把result统一提取，不利于区分，所以我们稍微改一改代码：

# 引入模块
# 为了实现计算过程详细展示，只使用了数学计算模块numpy和画图模块matplotlib
import numpy as np
import matplotlib.pyplot as plt# --------------------------
# 1. 定义输入和卷积核（简化尺寸便于观察）
# --------------------------
# 输入图像：4x4的简单矩阵（模拟灰度图）
input_image = np.array([[1, 2, 3, 0],[4, 5, 6, 0],[7, 8, 9, 0],[0, 0, 0, 0]
], dtype=np.float32)
# 先输出一下原始图像
plt.imshow(input_image, cmap='gray', vmin=0, vmax=9)
# 卷积核：2x2（用于提取简单特征）
kernel = np.array([[1, 0],[0, -1]
], dtype=np.float32)# 步长手动设置，可以改变
stride = 1  # 步长为1# --------------------------
# 2. 手动计算卷积过程并记录每一步
# --------------------------
# 用input_h, input_w分别提取原始图像input_image的高度和长度
input_h, input_w = input_image.shape
# 用kernel_h, kernel_w分别提取卷积核kernel的高度和长度
kernel_h, kernel_w = kernel.shape
# 先计算差分，可以知道原始矩阵和卷积核的大小差多少
# 实际上差多少，卷积核就要滑动多少步
# 但在最开始的时候，卷积核天然的就可以覆盖原始矩阵的一部分，因为覆盖，所以差分=0
# 所以这一步已经存在了，所以实际的步骤还要+1
out_h = (input_h - kernel_h) // stride + 1  # 输出高度：3
out_w = (input_w - kernel_w) // stride + 1  # 输出宽度：3# 存储每一步的滑动窗口和计算结果
steps1 = []  # 每个元素是 (窗口区域, 计算过程字符串, 结果值)
steps2 = []  # 每个元素是 (窗口区域, 计算过程字符串, 结果值)
# 卷积计算过程
for i in range(out_h):for j in range(out_w):# 提取当前滑动窗口（输入的局部区域）start_i, start_j = i * stride, j * stride# 因为+ kernel_h和+ kernel_w，实现真正的滑动# 这里实际上将每一小块元素都单独取出来了，就是windowswindow = input_image[start_i:start_i + kernel_h, start_j:start_j + kernel_w]# 计算卷积：元素相乘再求和product = window * kernel  # 元素相乘result1 = np.sum(product)  # 求和# 记录计算过程（用于可视化）# 由于取出来的windows大小都是2行2列，所以实现计算的过程中只需要关注[0,0],[0,1],[1,0]和[1,1]这四个位置# 先算第一行calc_str = f"({window[0, 0]}×{kernel[0, 0]}) + ({window[0, 1]}×{kernel[0, 1]}) + \n"# 再算第二行calc_str += f"({window[1, 0]}×{kernel[1, 0]}) + ({window[1, 1]}×{kernel[1, 1]}) = \n"# 将前两步计算获得的结果相加calc_str += f"({product[0, 0]}) + ({product[0, 1]}) + ({product[1, 0]}) + ({product[1, 1]}) ="result2=calc_str# 保存所有元素steps1.append(result1)steps2.append(result2)print('result1=',steps1)
print('result2=',steps2)

代码的运行效果也很有趣：

result1= [np.float32(-4.0), np.float32(-4.0), np.float32(3.0), np.float32(-4.0), np.float32(-4.0), np.float32(6.0), np.float32(7.0), np.float32(8.0), np.float32(9.0)]
result2= ['(1.0×1.0) + (2.0×0.0) + \n(4.0×0.0) + (5.0×-1.0) = \n(1.0) + (0.0) + (0.0) + (-5.0) =', '(2.0×1.0) + (3.0×0.0) + \n(5.0×0.0) + (6.0×-1.0) = \n(2.0) + (0.0) + (0.0) + (-6.0) =', '(3.0×1.0) + (0.0×0.0) + \n(6.0×0.0) + (0.0×-1.0) = \n(3.0) + (0.0) + (0.0) + (-0.0) =', '(4.0×1.0) + (5.0×0.0) + \n(7.0×0.0) + (8.0×-1.0) = \n(4.0) + (0.0) + (0.0) + (-8.0) =', '(5.0×1.0) + (6.0×0.0) + \n(8.0×0.0) + (9.0×-1.0) = \n(5.0) + (0.0) + (0.0) + (-9.0) =', '(6.0×1.0) + (0.0×0.0) + \n(9.0×0.0) + (0.0×-1.0) = \n(6.0) + (0.0) + (0.0) + (-0.0) =', '(7.0×1.0) + (8.0×0.0) + \n(0.0×0.0) + (0.0×-1.0) = \n(7.0) + (0.0) + (0.0) + (-0.0) =', '(8.0×1.0) + (9.0×0.0) + \n(0.0×0.0) + (0.0×-1.0) = \n(8.0) + (0.0) + (0.0) + (-0.0) =', '(9.0×1.0) + (0.0×0.0) + \n(0.0×0.0) + (0.0×-1.0) = \n(9.0) + (0.0) + (0.0) + (-0.0) =']

result1是直接的计算结果，result2是每一步的计算过程。

【3】卷积值绘图

既然新的卷积值也是好几个数，那就用一种简单的办法，把这几个数组合一下，展示为图像。

由于代码已经告诉我们，卷积核横向上会卷积计算out_h = (input_h - kernel_h) // stride + 1 次，纵向上会卷积计算out_w = (input_w - kernel_w) // stride + 1，很简单，我们就直接定义一个out_w列，out_h行的矩阵存储卷积计算值，然后用这个矩阵输出一张图像。

# 先定义一个纯0矩阵
output_image = np.zeros((out_h,out_w),dtype=np.float32)

然后在每一次计算的过程中，都直接把计算结果存储在纯0矩阵中：

# 卷积计算过程
for i in range(out_h):for j in range(out_w):# 提取当前滑动窗口（输入的局部区域）start_i, start_j = i * stride, j * stride# 因为+ kernel_h和+ kernel_w，实现真正的滑动# 这里实际上将每一小块元素都单独取出来了，就是windowswindow = input_image[start_i:start_i + kernel_h, start_j:start_j + kernel_w]# 计算卷积：元素相乘再求和product = window * kernel  # 元素相乘result1 = np.sum(product)  # 求和# 对于每次卷积计算，都把计算结果赋值给对应位置的纯0矩阵output_image[i,j]=result1

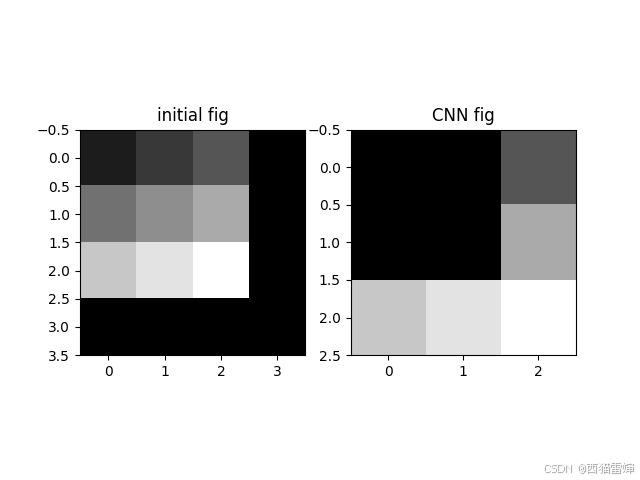
最后把原始图像和卷积计算的图像并列展示：

plt.figure()
plt.subplot(121)
# 先输出一下原始图像
plt.imshow(input_image, cmap='gray', vmin=0, vmax=9)
plt.title('initial fig')
plt.subplot(122)
# 先输出一下原始图像
plt.imshow(output_image, cmap='gray', vmin=0, vmax=9)
plt.title('CNN fig')plt.show()

效果为：

此时的完整代码为：

# 引入模块
# 为了实现计算过程详细展示，只使用了数学计算模块numpy和画图模块matplotlib
import numpy as np
import matplotlib.pyplot as plt# --------------------------
# 1. 定义输入和卷积核（简化尺寸便于观察）
# --------------------------
# 输入图像：4x4的简单矩阵（模拟灰度图）
input_image = np.array([[1, 2, 3, 0],[4, 5, 6, 0],[7, 8, 9, 0],[0, 0, 0, 0]
], dtype=np.float32)# 卷积核：2x2（用于提取简单特征）
kernel = np.array([[1, 0],[0, -1]
], dtype=np.float32)# 步长手动设置，可以改变
stride = 1  # 步长为1# --------------------------
# 2. 手动计算卷积过程并记录每一步
# --------------------------
# 用input_h, input_w分别提取原始图像input_image的高度和长度
input_h, input_w = input_image.shape
# 用kernel_h, kernel_w分别提取卷积核kernel的高度和长度
kernel_h, kernel_w = kernel.shape
# 先计算差分，可以知道原始矩阵和卷积核的大小差多少
# 实际上差多少，卷积核就要滑动多少步
# 但在最开始的时候，卷积核天然的就可以覆盖原始矩阵的一部分，因为覆盖，所以差分=0
# 所以这一步已经存在了，所以实际的步骤还要+1
out_h = (input_h - kernel_h) // stride + 1  # 输出高度：3
out_w = (input_w - kernel_w) // stride + 1  # 输出宽度：3# 先定义一个纯0矩阵
output_image = np.zeros((out_h,out_w),dtype=np.float32)
# 存储每一步的滑动窗口和计算结果
steps1 = []  # 每个元素是 (窗口区域, 计算过程字符串, 结果值)
steps2 = []  # 每个元素是 (窗口区域, 计算过程字符串, 结果值)
# 卷积计算过程
for i in range(out_h):for j in range(out_w):# 提取当前滑动窗口（输入的局部区域）start_i, start_j = i * stride, j * stride# 因为+ kernel_h和+ kernel_w，实现真正的滑动# 这里实际上将每一小块元素都单独取出来了，就是windowswindow = input_image[start_i:start_i + kernel_h, start_j:start_j + kernel_w]# 计算卷积：元素相乘再求和product = window * kernel  # 元素相乘result1 = np.sum(product)  # 求和# 对于每次卷积计算，都把计算结果赋值给对应位置的纯0矩阵output_image[i,j]=result1# 记录计算过程（用于可视化）# 由于取出来的windows大小都是2行2列，所以实现计算的过程中只需要关注[0,0],[0,1],[1,0]和[1,1]这四个位置# 先算第一行calc_str = f"({window[0, 0]}×{kernel[0, 0]}) + ({window[0, 1]}×{kernel[0, 1]}) + \n"# 再算第二行calc_str += f"({window[1, 0]}×{kernel[1, 0]}) + ({window[1, 1]}×{kernel[1, 1]}) = \n"# 将前两步计算获得的结果相加calc_str += f"({product[0, 0]}) + ({product[0, 1]}) + ({product[1, 0]}) + ({product[1, 1]}) ="result2=calc_str# 保存所有元素steps1.append(result1)steps2.append(result2)print('result1=',steps1)
print('result2=',steps2)plt.figure()
plt.subplot(121)
# 先输出一下原始图像
plt.imshow(input_image, cmap='gray', vmin=0, vmax=9)
plt.title('initial fig')
plt.subplot(122)
# 先输出一下原始图像
plt.imshow(output_image, cmap='gray', vmin=0, vmax=9)
plt.title('CNN fig')plt.show()

【4】细节说明

提取图像的像素使，其实得到的数第一个是行数，第二个是列数，行数对应图像的高，列数对应图像的宽，一定要小心辨别，以免用反。

【5】总结

学习了对卷积值进行提取的基本技巧。

http://www.dtcms.com/a/491009.html

相关文章：

  • [Android] Alarm Clock Pro 11.1.0一款经典简约个性的时钟
  • 【机器学习算法篇】K-近邻算法
  • K8S高可用集群-二进制部署 + nginx-proxy静态Pod版本
  • 使用Open CASCADE和BRepOffsetAPI_MakePipeShell创建螺旋槽钻头三维模型
  • 邯郸网站制作多少钱网站如何收录
  • 如何区分Android、Android Automotive、Android Auto
  • 企业融资方式有哪几种淄博网站seo价格
  • python - 第五天
  • 凡科网的网站建设怎么做网站 建设 公司
  • 透过浏览器原理学习前端三剑客：HTML、CSS与JavaScript
  • 镇江市网站建设江西省建设厅教育网站上查询
  • dede网站怎么设置首页相亲网站透露自己做理财的女生
  • Docker在已经构建好的镜像中安装包
  • 智慧物流赛项竞赛内容与技能要求深度解析
  • GPU散热革命：NVIDIA微通道液冷板（MLCP）技术深度解析
  • Docker安装部署MySQL一主二从集群
  • 搭建网站服务器多少钱网站在建设中是什么意思
  • Java 11对集合类做了哪些增强？
  • SQLSugar框架数据库优先
  • 工程建设教育网站北京网站建设cnevo
  • Vector数据库性能大比武：Pinecone、Weaviate、Chroma速度与准确率实测
  • 天津老区建设促进会网站移动开发的现状和前景
  • 笔试强训(六)
  • Iterator迭代器 【ES6】
  • spring boot实现接口数据脱敏，整合jackson实现敏感信息隐藏脱敏
  • 基于单片机的汽车多参数安全检测与报警系统设计
  • C++设计模式_行为型模式_备忘录模式Memento
  • 温州h5建站关于网站建设的文章
  • 大连专业做网站wordpress 4.5 汉化主题
  • Spring Boot 3零基础教程，Spring Boot 日志分组，笔记20