当前位置：首页 > news >正文

【数据结构——最小生成树与Kruskal】

news 2025/10/15 11:21:31

引入

最小生成树（Minimum Spanning Tree, MST）是无向连通图中一棵包含所有顶点的生成树，且其边的权值之和最小。

最小生成树的性质
连通性：包含图中所有顶点。
无环性：是一棵树，不包含任何环路。
最小权值和：所有边的权值总和在所有可能的生成树中最小。

简单来说就是：边是无向连通全部顶点且不成环,顶点n个边(n-1)个,权和最低。
注意：最小生成树的结构不唯一。

加边细则

选边要求：优先加权值最小的边，直到加够(n-1)条边为止。
加边要求：加上边不成环。
判断是否成环（验证）：

边与边通过顶点形成一条连线，将此线经由的所有顶点都看成是一个集合的
集合与集合之间若不相通，则两集合之间可以添加一条边（每次添加一条）

判断加边后是否成环（加边判断）：
利用并查集（quickUnion）的思想（回顾quickUnion）:找每个节点的根节点，同根不连（不加边）。

实现

首先为了方便存储无向图的权值，图用邻接矩阵表示；其次利用邻接矩阵创建边集数组；最后是利用边集数组完成Kruskal算法的实现。
实现思路：

进行加边操作前要以权值大小为标准从小到大排序
依次判断加上边是否成环：
不成的话这条边就归入生成树的组成部分；
成环就再找下一条边再次判断。

头文件

common.h

//边集数组结构
typedef struct {int begin;   //起点int end;     //终点int weight;  //权值
}EdgeSet;

Kruskal.h

#include"common.h"
#include"matrixGraph.h"//从邻接矩阵中初始化边集数组
void InitEdgeSet(const MGraph* graph, EdgeSet* edges);//排序边集数组
void sortEdgeSet(EdgeSet* edges, int num);//Kruskal算法
int KruskalMGraph(const EdgeSet* edges, int num, int node_num, EdgeSet* result);

功能实现

补充：
memcpy 与 strcpy 的区别

功能差异
memcpy 用于复制任意内存块，不关心数据内容（如字符串、结构体、数组等）。strcpy 专门用于复制以 \0 结尾的字符串，遇到 \0 自动停止。
参数差异
memcpy(void* dest, const void* src, size_t n)：需指定复制的字节数 n。
strcpy(char* dest, const char* src)：无需指定长度，自动根据 \0 判断结束。
安全性
memcpy 需手动确保目标缓冲区足够大，否则可能溢出。strcpy 同样存在溢出风险，但更易因缺失 \0 导致问题。

#include"Kruskal.h"
#include<stdio.h>
#include<stdlib.h>
#include<string.h>

初始化边集数组

void InitEdgeSet(const MGraph* graph, EdgeSet* edges) {int k = 0;for (int i = 0; i < graph->nodeNum; ++i) {for (int j = i + 1; j < graph->nodeNum; ++j) {if (graph->edge[i][j] > 0) {edges[k].begin = i;edges[k].end = j;edges[k].weight = graph->edge[i][j];k++;}}}
}

边集数组排序

void sortEdgeSet(EdgeSet* edges, int num) {EdgeSet tmp;for (int i = 0; i < num; ++i) {for (int j = i + 1; j < num; ++j) {if (edges[j].weight < edges[i].weight) {memcpy(&tmp, &edges[i], sizeof(EdgeSet));memcpy(&edges[i], &edges[j], sizeof(EdgeSet));memcpy(&edges[j], &tmp, sizeof(EdgeSet));}}}
}

代码通过循环不断向上追溯父节点，直到找到根节点：
初始化时传入参数 a，表示需要查找根节点的元素。
检查当前元素 a 的父节点是否等于自身。若不等，则将 a 更新为其父节点，继续循环。
当 uSet[a] == a 时，说明已到达根节点，退出循环并返回 a。

找根

static int getRoot(const int* uSet, int a) {if (uSet == NULL) {printf("malloc failed!\n");return -1;}while (uSet[a] != a) {a = uSet[a];}// 退出循环时，uSet[a] == a，即 a 是根节点return a;
}

Kruskal实现

int KruskalMGraph(const EdgeSet* edges, int num, int node_num, EdgeSet* result) {int* uSet;int count = 0;int sum = 0;//1.初始化并查集uSet =(int*) malloc(sizeof(int) * node_num);if (uSet == NULL) {printf("malloc failed!\n");return -1;}for (int i = 0; i < node_num; ++i) {uSet[i] = i;}//2.从已经排列好的边集中找边的起始节点的根，判断是否成环for (int i = 0; i < num; ++i) {int a = getRoot(uSet, edges[i].begin);int b = getRoot(uSet, edges[i].end);if (a != b) {uSet[a] = b; //将a的父节点设为bresult[count].begin = edges[i].begin;result[count].end = edges[i].end;result[count].weight = edges[i].weight;sum += edges[i].weight;count++;if (count == node_num - 1) {break;}}}free(uSet);return sum;
}

main函数

图的创建

void setupMGraph(MGraph* graph) {//                  0    1    2    3    4    5    6const char* names[] = {"A", "B", "C", "D", "E", "F", "G"};initMGraph(graph, names, sizeof(names) / sizeof(names[0]), 0, 0);addMGraphEdge(graph, 0, 1, 12);addMGraphEdge(graph, 0, 5, 16);addMGraphEdge(graph, 0, 6, 14);addMGraphEdge(graph, 1, 2, 10);addMGraphEdge(graph, 1, 5, 7);addMGraphEdge(graph, 2, 3, 3);addMGraphEdge(graph, 2, 4, 5);addMGraphEdge(graph, 2, 5, 6);addMGraphEdge(graph, 3, 4, 4);addMGraphEdge(graph, 4, 5, 2);addMGraphEdge(graph, 4, 6, 8);addMGraphEdge(graph, 5, 6, 9);
}

功能调用

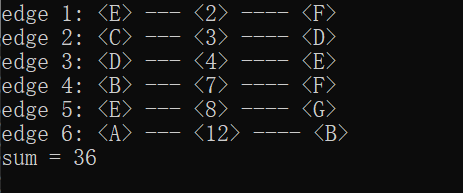
void test251014() {MGraph graph;EdgeSet* edges;EdgeSet* result;setupMGraph(&graph);edges = (EdgeSet*)malloc(sizeof(EdgeSet) * graph.edgeNum);if (edges == NULL) {return;}InitEdgeSet(&graph, edges);sortEdgeSet(edges, graph.edgeNum);result = (EdgeSet*)malloc(sizeof(EdgeSet) * (graph.nodeNum - 1));if (result == NULL) {//edges是先前malloc分配的边集数组,属于中间结果。// 若后续关键内存分配（如result）失败，整个操作无法完成，中间结果便失去意义。// 释放edges符合“申请失败即回滚”的防御性编程原则。free(edges);   //回滚return;}int sum = KruskalMGraph(edges, graph.edgeNum, graph.nodeNum, result);for (int i = 0; i < graph.nodeNum - 1; i++) {printf("edge %d: <%s> --- <%d> ---- <%s>\n", i + 1,graph.vex[result[i].begin].show, result[i].weight, graph.vex[result[i].end].show);}printf("sum = %d\n", sum);free(result);free(edges);
}