【数值分析】非线性方程与方程组的数值解法的经典算法(附MATLAB代码)
1. 二分法
算法原理:确定 f(x) 的有根区间 [a,b] 后,反复二分区间并缩小有根区间长度;当区间长度或中点函数值满足精度时停止。
算法步骤:
a. 给定有根区间 [a,b] 及精度 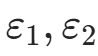 ;
;
b. 若 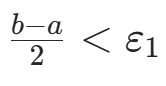 ,取
,取 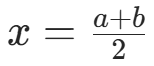 ,结束;
,结束;
c. 取 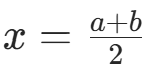 ,若
,若 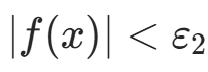 ,结束;
,结束;
d. 若 f(a)⋅f(x)<0,则 b=x,否则 a=x,转 b。
MATLAB 程序:
function [x, it] = bisect(fun, a, b, ep1, ep2)
if nargin < 4ep1 = 1e-5; ep2 = 1e-5;
end
fa = feval(fun, a); fb = feval(fun, b);
if fa * fb > 0x = [fa, fb]; it = 0; return;
end
k = 1;
while abs(b - a)/2 > ep1x = (a + b)/2; fx = feval(fun, x);if abs(fx) < ep2 return; endif fx * fa < 0b = x; fb = fx;elsea = x; fa = fx;endk = k + 1;
end
it = k;
数值实验
例 1:求 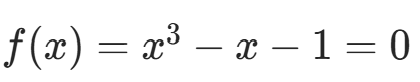 在 (1.0,1.5) 内的实根。
在 (1.0,1.5) 内的实根。
>> fun = inline('x^3 - x - 1'); [x, it] = bisect(fun, 1, 1.5)
2. 不动点迭代法
算法原理:由迭代函数 φ(x) 及初始值 ![]() ,通过
,通过 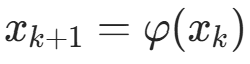 迭代,直到满足精度或达到最大迭代次数。
迭代,直到满足精度或达到最大迭代次数。
算法步骤:
a. 给定 φ(x)、初始值 ![]() 、精度 ε、最大迭代次数 it_max;
、精度 ε、最大迭代次数 it_max;
b. 计算 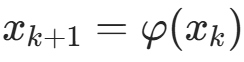 ;
;
c. 若 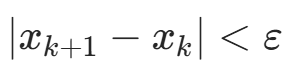 ,结束;
,结束;
d. 否则 k=k+1,转 b(若达最大次数则结束)。
MATLAB 程序:
function [x, it] = iterate(phi, x0, ep, it_max)
if nargin < 4 it_max = 100; end
if nargin < 3 ep = 1e-5; end
k = 1;
while k < it_maxx1 = feval(phi, x0);if abs(x0 - x1) < ep break; endk = k + 1; x0 = x1;
end
x = x1; it = k;
数值实验
例 2:求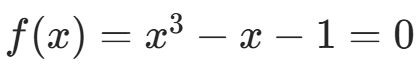 在
在 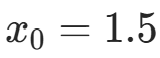 附近的根(迭代函数
附近的根(迭代函数 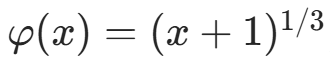 )。
)。
>> phi = inline('(x + 1)^(1/3)'); [x, it] = iterate(phi, 1.5)

3. 斯特芬森迭代法
算法原理:用加速公式 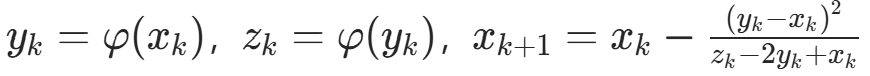 迭代,加速收敛。
迭代,加速收敛。
算法步骤:
a. 给定 φ(x)、初始值 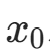 、精度 ε、最大迭代次数 it_max;
、精度 ε、最大迭代次数 it_max;
b. 计算 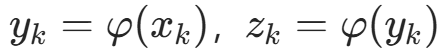 ;
;
c. 计算 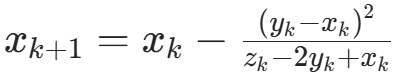 ;
;
d. 若 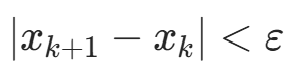 ,结束;
,结束;
e. 否则 k=k+1,转 b(若达最大次数则结束)。
MATLAB 程序:
function [x, it] = steffensen(phi, x0, ep, it_max)
if nargin < 4 it_max = 100; end
if nargin < 3 ep = 1e-5; end
k = 1;
while k < it_maxx1 = x0; y = feval(phi, x0); z = feval(phi, y); x0 = x0 - (y - x0)^2 / (z - 2 * y + x0);if abs(x0 - x1) < ep break; endk = k + 1;
end
x = x0; it = k;
数值实验
例 3:求 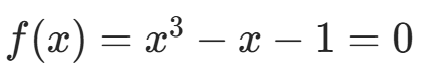 在
在 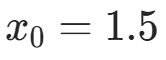 附近的根(迭代函数
附近的根(迭代函数 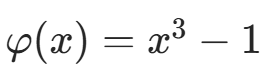 )。
)。
>> phi = inline('x^3 - 1'); [x, it] = steffensen(phi, 1.5)
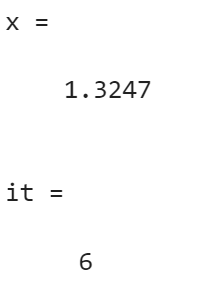
4. 牛顿法
算法原理:由初始值 ![]() ,通过
,通过 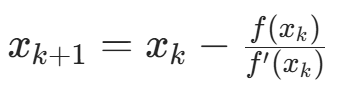 迭代,直到满足精度或达到最大迭代次数。
迭代,直到满足精度或达到最大迭代次数。
算法步骤:
a. 给定初始值 ![]() 、精度 ε、最大迭代次数 it_max;
、精度 ε、最大迭代次数 it_max;
b. 计算 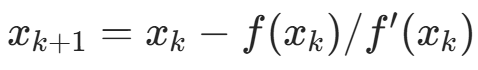 ;
;
c. 若 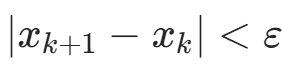 ,结束;
,结束;
d. 否则 k=k+1,转 b(若达最大次数则结束)。
MATLAB 程序:
function [x, it] = Newton(fun, x0, ep, it_max)
if nargin < 4 it_max = 100; end
if nargin < 3 ep = 1e-5; end
k = 1;
while k < it_maxx1 = x0; f = feval(fun, x0); x0 = x0 - f(1)/f(2);if abs(x0 - x1) < ep break; endk = k + 1;
end
x = x0; it = k;
说明:调用前需将 f(x) 和 f′(x) 以向量形式赋值给 fun。
数值实验
例 4:求 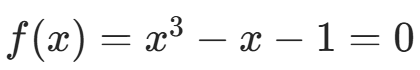 在
在 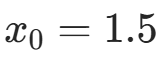 附近的根。
附近的根。
>> fun = inline('[x^3 - x - 1, 3 * x^2 - 1]'); [x, it] = Newton(fun, 1.5)

总结
本文介绍了四种数值求解非线性方程的算法及其MATLAB实现。二分法通过不断缩小有根区间来逼近根;不动点迭代法利用迭代函数逐步逼近解;斯特芬森迭代法采用加速公式提高收敛速度;牛顿法结合函数值和导数信息快速收敛。每种算法都给出了原理说明、实现步骤和MATLAB程序,并通过数值实验验证了有效性。这些方法适用于不同精度要求和收敛特性的非线性方程求解问题。
