数据库设计基础知识（3）关系运算

关系操作的特点是操作对象和操作结果都是集合。

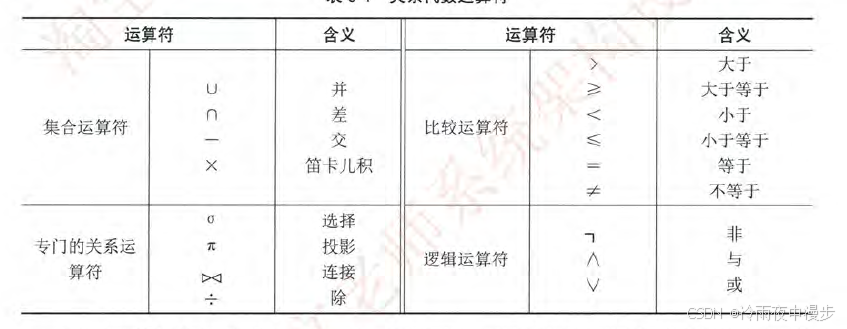
关系代数运算符有4类：集合运算符、专门的关系运算符、算术比较符和逻辑运算符。

并

关系R与S具有相同的关系模式，即R与S的元数相同(结构相同)。关系R与S的并由属于R或属于S的元组构成的集合组成，记作RUS,其形式定义如下，式中t为元组变量。
R ∪ S = { t ∣ t ∈ R ∨ t ∈ S } R \cup S=\{t|t \in R \lor t \in S\} R∪S={t∣t∈R∨t∈S}

差

关系R与S具有相同的关系模式，关系R与S的差是由属于R但不属于S的元组构成的集合，记作R-S,其形式定义如下：
R − S = { t ∣ t ∈ R ∧ t ∉ S } R-S=\{ t|t \in R \land t \notin S\} R−S={t∣t∈R∧t∈/S}

交

关系R与S具有相同的关系模式，关系R与S的交是由属于R同时又属于S的元组构成的
集合，关系R与S的交可记为R∩S,其形式定义如下：
R ∩ S = { t ∣ t ∈ R ∧ t ∈ S } R \cap S = \{ t|t \in R \land t \in S \} R∩S={t∣t∈R∧t∈S}
显然：
$$R\cap S=R-(R-S)或R\cap S=S-(S-R)$$

笛卡尔积

两个元数分别为n目和m目的关系R和S的广义笛卡尔积是一个(n+m)列的元组的集合。元组的前n列是关系R的一个元组，后m列是关系S的一个元组，记作RXS,其形式定义如下：
KaTeX parse error: Undefined control sequence: \and at position 33: …|t=<t^n, t^m > \̲a̲n̲d̲ ̲t^n \ in R\ \}

笛卡尔积在SQL应用上为：多表查询或者没有指定筛选条件（或筛选条件恒为真）的JOIN连接

SELECT * 
FROM 表1, 表2;  -- 表1和表2的笛卡尔积SELECT * 
FROM 表1
CROSS JOIN 表2;  -- 表1和表2的笛卡尔积-- 无筛选条件的INNER JOIN，等价于笛卡尔积
SELECT * 
FROM 表A
INNER JOIN 表B ON 1=1;  -- 1=1是恒真条件，无实际筛选作用

选择

选择运算是从关系的水平方向进行运算，是从关系R中选择满足给定条件的诸元组，记作σF®,其形式定义如下：
σ F ( R ) = { t ∣ t ∈ R ∧ F ( t ) = T r u e } 其中， F 中的运算对象是属性名 ( 或列的序号 ) 或常数，由运算符、算术比较符 ( < 、 ≤ 、 > 、 ≥ 、 ≠ ) 和 逻辑运算符（ ∧ 、 ∨ 、 ¬ ）构成。例如， σ 1 ≥ 6 ( R ) 表示选取 R 关系中第 1 个属性值大于等于第 6 个属性值的元组 σ 1 ≥ ′ 6 ′ ( R ) 表示选取 R 关系中第 1 个属性值大于等于 6 的元组。 \sigma_F(R) = \{t|t \in R \land F(t)=True\}\\ 其中，F中的运算对象是属性名(或列的序号)或常数，由运算符、算术比较符(<、≤、>、≥、≠)和\\ 逻辑运算符（\land、\lor、\lnot）构成。例如，\sigma_{1≥6}(R)表示选取R关系中第1个属 性值大于等于第6个属性值的元组\\ \sigma_{1≥'6'}(R)表示选取R关系中第1个属性值大于等于6的元组。 σF​(R)={t∣t∈R∧F(t)=True}其中，F中的运算对象是属性名(或列的序号)或常数，由运算符、算术比较符(<、≤、>、≥、=)和逻辑运算符（∧、∨、¬）构成。例如，σ1≥6​(R)表示选取R关系中第1个属性值大于等于第6个属性值的元组σ1≥′6′​(R)表示选取R关系中第1个属性值大于等于6的元组。

投影

投影运算是从关系的垂直方向进行运算，在关系R中选择出若干属性列A组成新的关系，记作πA®,其形式定义如下：
π A ( R ) = { t [ A ] ∣ t ∈ R } \pi_A(R)=\{t[A]|t \in R\} πA​(R)={t[A]∣t∈R}

连接

连接分为θ连接、等值连接及自然连接3种。连接运算是从两个关系R和S的笛卡尔积中选取满足条件的元组。因此，可以认为笛卡尔积是无条件连接，其他的连接操作是有条件连接。

• θ连接：θ连接是从R与S的笛卡尔积中选取属性满足一定条件的元组。其形式定义如下：
  KaTeX parse error: Undefined control sequence: \and at position 63: …|t=<t^n, t^m > \̲a̲n̲d̲ ̲t^n \in R \and …

  $$\begin{gathered} 其中：X\theta Y为连接的条件，\theta 是比较运算符，X和Y分别表示为R和S上度数相等，且可比的属性组。 \\ {t}^n[X]表示R中t^n元组的相应于属性X的一个分量。t^m[Y]表示S中t^m元组的相应于属性Y的一个分量 \end{gathered}$$

  θ连接也可以表示为：
  KaTeX parse error: Undefined control sequence: \and at position 63: …|t=<t^n, t^m > \̲a̲n̲d̲ ̲t^n \in R \and …

  $$\begin{gathered} 其中：i=1,2,3,...,n,j=1,2,3,...,m，i\theta j的含义为从两个关系R和S中选取R的第i列和S的第j列 \\ 之间满足\theta 运算的元组进行连接 \end{gathered}$$

  θ连接也可以由基本的关系运算笛卡尔积和选取运算导出：
  $$R\underset{X\theta Y}{\bowtie }S={\sigma }_{X\theta Y}(R\times S)或R\underset{i\theta j}{\bowtie }S={\sigma }_{i\theta (i+j)}(R\times S)$$
  从上可以看出θ 连接的本质：

  θ 连接 = 笛卡尔积 + 基于 θ 运算符的选择条件，解决了笛卡尔积的冗余问题；θ定义连接条件的比较类型（等值 / 不等值）；SQL 中的 JOIN 操作（如 INNER JOIN ... ON 条件）本质就是 θ 连接的实现，其中 ON 后的条件即 θ 连接条件。

  SELECT * 
  FROM 表A
  INNER JOIN 表B ON 表A.字段1>表B.字段1;
  

• 等值连接：当θ定义连接条件为等值"="时，称为等值连接，其定义如下：
  KaTeX parse error: Undefined control sequence: \and at position 58: …|t=<t^n, t^m > \̲a̲n̲d̲ ̲t^n \in R \and …

  SELECT * 
  FROM 表A
  INNER JOIN 表B ON 表A.字段1=表B.字段1;
  

• 自然连接：特殊等值连接，要求连接属性同名，且去重重复列；
  KaTeX parse error: Undefined control sequence: \and at position 260: …|t=<t^n, t^m > \̲a̲n̲d̲ ̲t^n \in R \and …
  自然连接可以由基本的关系运算笛卡尔积和选取运算导出，因此自然连接可表示为：
  $$R\bowtie S={\prod }_{A_1,A_2,...,A_n-k},R.B_1,R.B_2,...,R.B_K,B_{K+1},B_{K+2},...,B_m({\sigma }_{R.B_1=S.B1,R.B_2=S.B_2,...,R.B_K=S.B_K}(R\times S))$$
  因为自然连接要去掉重复属性，如果没有重复属性，那么自然连接就转化为笛卡儿积。

除

除运算同时从关系的水平方向和垂直方向进行运算。给定关系R(X,Y)和S(Y,Z)，X、Y、Z为属性组。R÷S应当满足元组在X上的分量值x的象集Y,包含关系S在属性组Y上投影的集合。其形式定义如下：
KaTeX parse error: Undefined control sequence: \and at position 31: …n[X]|t^n \in R \̲a̲n̲d̲ ̲\pi_y(S)\subset…
除运算的本质是 “筛选 X 的值，使其对应的 Y 值覆盖 S 中所有 Y 值”。

实例：用除运算解决实际问题

假设我们有两个关系，用于查询 “选修了所有必修课的学生”：

关系 1：学生选课表 R（属性：学号 X，课程号 Y）

学号（X）	课程号（Y）
202301	Math
202301	English
202301	Physics
202302	Math
202302	English
202303	Math
202304	English

关系 2：必修课表 S（属性：课程号 Y）

课程号（Y）
Math
English

我们需要计算 R ÷ S，即 “选修了所有必修课（Math 和 English）的学生学号”。

广义投影(Generalized Projection)

广义投影运算允许在投影列表中使用算术运算，实现了对投影运算的扩充。
$$\begin{gathered} 若有关系R,条件F_1,F_2,\cdots ,F_n,中的每一个都是涉及R中常量和属性的算术表达式， \\ 那么广义投影运算的形式定义为：{\pi }_{F_1,F_2,\cdots ,F_n}(R)。 \end{gathered}$$

外连接

外连接运算是连接运算的扩展，可以处理缺失的信息。外连接运算有三种：左外连接、右外连接和全外连接。

• 左外连接(Left Outer Jion)
  左外连接：取出左侧关系中所有与右侧关系中任一元组都不匹配的元组，用空值null充填所有来自右侧关系的属性，构成新的元组，将其加入自然连接的结果中。
• 右外连接(Right Outer Jion)KI
  右外连接：取出右侧关系中所有与左侧关系中任一元组都不匹配的元组，用空值null填充所有来自左侧关系的属性，构成新的元组，将其加入自然连接的结果中。
• 全外连接(Full Outer Jion)J
  全外连接：完成左外连接和右外连接的操作。即填充左侧关系中所有与右侧关系中任一元组都不匹配的元组，又填充右侧关系中所有与左侧关系中任一元组都不匹配的元组，将产生的新元组加入自然连接的结果中。

聚集函数

聚集运算是关系代数运算中的一个非常重要的扩展。聚集函数输入一个值的集合，返回单一值作为结果。例如，集合{2,4,6,8,10,15}。将聚集函数sum用于该集合时返回和45;将聚集函数avg用于该集合时返回平均值7.5;将聚集函数count用于该集合时返回集合中元数的个数6;将聚集函数min用于该集合时返回最小值2;将聚集函数max用于该集合时返回最大值15。