Generalized Sparse Additive Model with Unknown Link Function
文章:《Generalized Sparse Additive Model with Unknown Link Function》
基于双层优化下,未知链接函数的广义稀疏可加模型
背景: 可加模型是经典的统计建模方式,并且近些年在众多(人工智能 / 统计 / 数学)顶刊定会上有对应的工作,完善了更多的建模以及理论工作。它享有着天然的可解释性!
研究背景
广义可加模型(GAM)在高维数据分析中得到了广泛应用,能够有效解决变量对响应的非线性影响问题。然而,现有方法大多无法同时估计链接函数、组件函数和变量交互。此外,实际数据中常用的链接函数可能不适用,导致组件函数估计偏差,影响模型预测。因此,本文提出了一种新的广义稀疏可加模型,能够同时估计未知链接函数和组件函数,并进行变量选择。

核心技术和思想
本文提出了一种名为广义稀疏可加模型(GSAMUL)的新模型,其核心技术和思想包括:
- 组件函数估计:使用B样条基函数(B-spline basis)估计组件函数。
- 链接函数估计:使用多层感知器(MLP)网络估计未知链接函数。
- 变量选择:通过ℓ2,1-范数正则化实现变量选择。
- 双层优化问题:将数据分为训练集和验证集,通过双层优化问题估计未知函数。
核心贡献

- 模型创新:提出了一种新的GAM模型,能够同时进行估计和变量选择,模型介于白盒和黑盒之间。
- 优化方案:提出了一个双层优化方案,用于估计未知链接函数和组件函数,并提供了优化算法的收敛性分析。
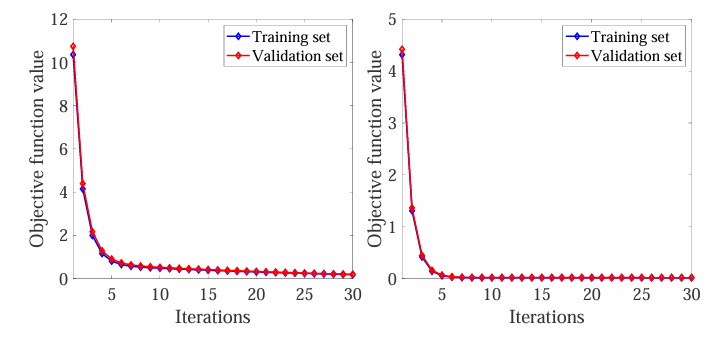
- 有效性验证:通过模拟数据和真实世界数据的实验评估,验证了GSAMUL在变量选择和函数估计方面的有效性,即使在数据受到无关变量污染的情况下也能高效工作。
解决的问题
GSAMUL解决了以下问题:
- 同时估计链接函数和组件函数:现有方法无法同时估计链接函数和组件函数,GSAMUL通过B样条和MLP网络实现了这一目标。
- 变量选择和交互学习:通过ℓ2,1-范数正则化实现变量选择,并通过MLP网络隐式学习变量之间的交互。
- 高维数据处理:在高维数据和复杂结构数据中,现有方法通常无法取得满意的结果,GSAMUL通过双层优化和正则化实现了对高维数据的有效处理。

