MATLAB三角模糊层次分析法在高校实验室评估中的应用
一、 核心思想与要解决的问题
1. 核心思想:
承认并量化人类判断的模糊性。在传统的AHP中,专家需要给出“A指标比B指标绝对重要(9分)”或“稍微重要(3分)”等精确判断。但在现实中,专家的判断更可能是“介于‘稍微重要’和‘明显重要’之间”。三角模糊数通过一个区间和一个最可能值来捕捉这种模糊判断。
2. 要解决的问题:
- 主观性过强: 传统AHP要求精确数值,忽略了专家思维的模糊性。
- 判断一致性难以保证: 当指标众多时,专家很难做出完全一致的精确判断。
- 信息损失: 将模糊的定性判断强行精确为一个数字,会损失部分信息,影响评估结果的科学性和可信度。
二、 应用步骤(技术路线)
将三角模糊层次分析法应用于高校实验室评估,通常遵循以下流程,其技术路线可通过下图清晰地展示:
flowchart TDA[构建高校实验室<br>评估指标体系] --> B[建立三角模糊判断矩阵]B --> C[计算模糊权重向量]C --> D[去模糊化<br>(转化为清晰值)]D --> E[清晰权重归一化]E --> F[计算各实验室<br>综合得分]F --> G[排序与决策支持]
下面我们对每个步骤进行具体说明:
步骤1:构建高校实验室评估指标体系
首先,建立一个全面、系统的评估指标体系。这是一个递阶层次结构,通常包括:
- 目标层(A): 高校实验室综合水平。
- 准则层(B): 支撑总目标的一级指标,如:
- B1:硬件设施与环境
- B2:科研与创新能力
- B3:教学与人才培养
- B4:管理水平与运行效率
- B5:安全与环保
- 指标层(C): 对准则层进一步细化,形成可操作、可衡量的具体指标。例如:
- C11(隶属于B1):设备先进性、设备完好率
- C21(隶属于B2):高水平论文数量、科研项目经费
- … …
步骤2:建立三角模糊判断矩阵
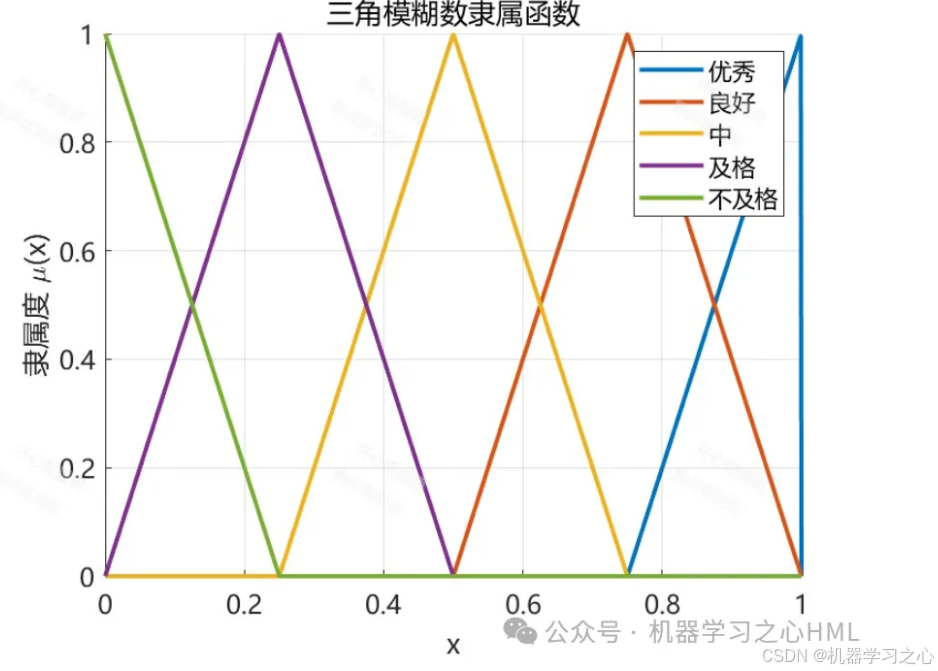
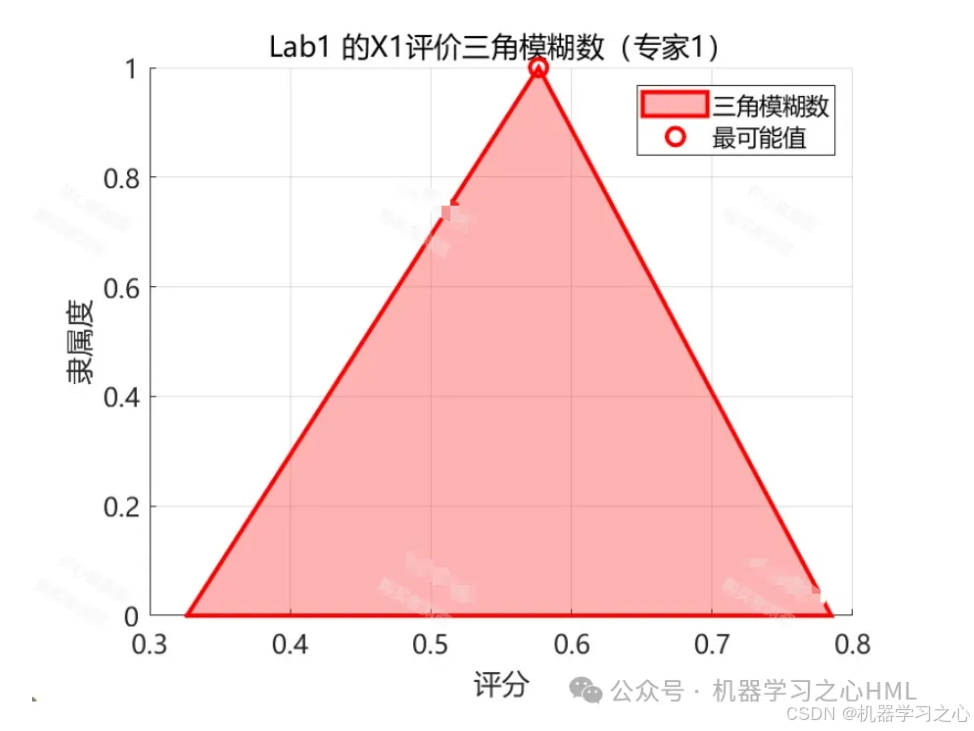
邀请评估专家(多位),使用三角模糊数来代替传统的1-9标度法进行两两比较。一个三角模糊数记为 (l, m, u):
- l(下界): 保守估计值。
- m(中值): 最可能的估计值。
- u(上界): 乐观估计值。
例如,一位专家认为“硬件设施(B1)”相对于“管理水平(B4)”的重要性介于“稍微重要(3)”和“明显重要(5)”之间,且最可能是“略微偏强(4)”,则可表示为 (3, 4, 5)。
综合所有专家的意见,通过几何平均等方法,构建出各个层次(如B层对A层,C层对B层)的综合三角模糊判断矩阵。
步骤3:计算模糊权重向量
对于每个三角模糊判断矩阵,采用特定的数学方法计算其模糊权重。常用方法有:
- 模糊特征值法
- 模糊几何平均法(相对简单常用):
- 计算每个准则的模糊综合值。
- 计算每个准则的模糊权重,它本身也是一个三角模糊数。
步骤4:去模糊化(解模糊)
为了便于比较和排序,需要将计算得到的模糊权重向量转化为清晰的数值。常用方法有:
- 重心法: 对于一个三角模糊数 (l, m, u),其清晰值 ( W = \frac{l + m + u}{3} )。这种方法简单直观。
- (\alpha)-截集法: 考虑决策者的风险态度,计算更复杂但更精确。
步骤5:清晰权重归一化
对去模糊化后得到的权重进行归一化处理,确保同一层级下所有指标的权重之和为1。
步骤6:计算各实验室综合得分
- 针对待评估的每个实验室,收集其在最底层指标(C层)上的原始数据(定量或定性打分)。
- 对原始数据进行标准化/无量纲化处理。
- 将标准化后的分数与对应的指标权重(从步骤5得来)进行加权求和,自下而上地逐层计算,最终得到每个实验室的综合得分。
步骤7:排序与决策支持
根据各实验室的综合得分进行排序,为学校的资源分配、绩效奖励、实验室建设与改进提供科学依据和决策支持。
三、 简单实例说明
假设仅评估两个准则:“硬件设施(B1)”和“科研创新(B2)”。
- 模糊判断矩阵(相对于总目标“实验室水平”):
- B1 / B2:专家综合意见为 (1, 2, 3) → 表示B1比B2“介于同样重要和稍微重要之间”。
- B2 / B1:自然就是 (1/3, 1/2, 1/1) ≈ (0.333, 0.5, 1.000)。
- 计算模糊权重(以几何平均法简化说明):
- B1的模糊综合值 ≈ ( \sqrt{(1 \times 1)} , \sqrt{(2 \times 0.5)} , \sqrt{(3 \times 1)} ) = (1, 1, 1.732)
- 归一化后得到B1、B2的模糊权重。
- 去模糊化(采用重心法):
- 假设B1的模糊权重为 (0.4, 0.6, 0.8),则清晰值 = (0.4+0.6+0.8)/3 = 0.6。
- 假设B2的清晰权重为0.4。
- 评估:实验室A在B1上得90分,在B2上得80分。则其综合得分 = 90×0.6 + 80×0.4 = 86。
四、 优势与价值
- 更符合实际: 有效处理专家判断中的模糊性和不确定性,使评估过程更贴近人类的真实思维模式。
- 提高评估科学性: 相比于传统AHP,它包含了更多的判断信息(下界、上界),减少了信息损失,使结果更可靠。
- 增强结果稳定性: 通过模糊数的区间表示,在一定程度上吸收了专家判断的波动,使排序结果更具鲁棒性。
- 决策支持能力强: 不仅能给出排名,还能通过分析模糊权重的区间,了解各指标重要性的可能波动范围,为决策者提供更深层次的洞察。
结论
三角模糊层次分析法为高校实验室这类复杂系统的综合评估提供了一个强有力的工具。它将定性与定量分析完美结合,通过严谨的数学方法处理模糊主观信息,最终得出一个更为科学、合理、可信的评估结果,极大地提升了高校实验室管理和决策的科学化水平。
