Tweedie 公式

学习路径

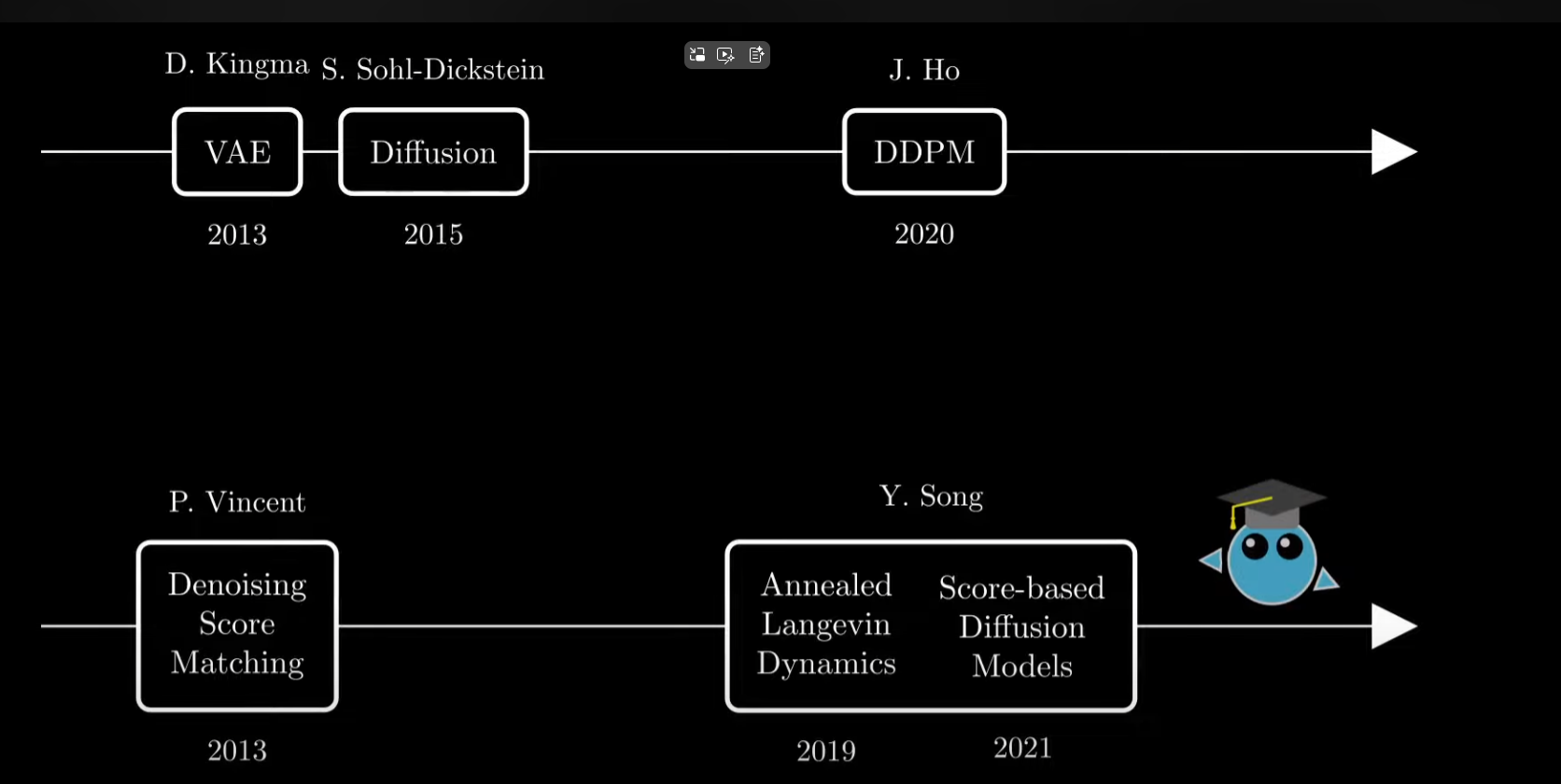
概论

Tweedie’s Formula（特维迪公式） 是这些Denoising Autoencoder、Score-based 模型 或 Diffusion Model 的理论基础背后“从噪声中恢复信号”的数学核心。

---

0. 场景与记号（全部变量的意义）

• $(x\in {\mathbb{R}}^d)$：真实的干净信号（先验 $p(x)$ 未知但假设良好）。
• $(y\in {\mathbb{R}}^d)$：观测（被噪声污染后的样本）。
• $\epsilon \in {\mathbb{R}}^d$：高斯噪声，$(\epsilon \sim \mathcal{N}(0,\Sigma ))$。
• $\Sigma \in {\mathbb{R}}^{d\times d}$：噪声协方差，对称正定。各向同性时 $\Sigma ={\sigma }^{2}I$。
• $p(x)$：先验密度；$(p(y\mid x)$：似然（由噪声模型）；$p(y)$：边际密度；$p(x\mid y)$：后验密度。
• ${\nabla }_y$：对向量 (y) 的梯度算子（见 §1 解释）。
• 目标是平方误差意义下的最优去噪：$\hat{x}(y):=\mathbb{E}[x\mid y]$。

噪声模型：$$y=x+\epsilon ,\epsilon \sim \mathcal{N}(0,\Sigma )\Rightarrow p(y\mid x)=\mathcal{N}(y;x,\Sigma )$$

---

1. 概念解释

1.1. ${\nabla }_y$ 向量梯度算子 是什么？

对标量函数 $(f:{\mathbb{R}}^d\to \mathbb{R})$，
$${\nabla }_{y}f(y)=\left[\begin{array}{c}\frac{\partial f}{\partial y_1}(y)\\ ⋮\\ \frac{\partial f}{\partial y_d}(y)\end{array}\right]\in {\mathbb{R}}^d.$$
它是所有一阶偏导的“向量打包”。几何意义：在点 $y$，${\nabla }_{y}f(y)$ 指向 $f$ 增长最快的方向，模长给出最大增长率。
在 Tweedie 里我们会用到 $s(y):={\nabla }_y\log p(y)$（score 函数）。

1.2. $\Sigma$ 协方差矩阵（Covariance Matrix）是什么

推荐好文：https://zhuanlan.zhihu.com/p/37609917

设有d组随机向量$${\mathbf{x}}_k={\left[\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_d\end{array}\right]}_{k}k=1,2,...,d$$
期望为对每个维度的数据求平均。
$$\mu =\mathbb{E}[\mathbf{x}]=\left[\begin{array}{c}\mathbb{E}[x_1]\\ \mathbb{E}[x_2]\\ ⋮\\ \mathbb{E}[x_d]\end{array}\right],\mathbb{E}[x_i]=\frac{1}{d}\sum _{k=1}^d{\mathbf{x}}_{k_{(i)}}$$
Σ 是在所有样本中，不同维度之间的方差和相关性结构，协方差为
$$\begin{gathered} \Sigma =\mathbb{E}[(\mathbf{x}-\mu )(\mathbf{x}-\mu {)}^T]=\mathbb{E}\left[\left[\begin{array}{c}{x}_1-{\mu }_1\\ x_2-{\mu }_2\\ ⋮\\ x_d-{\mu }_d\end{array}\right]\left[\begin{array}{c}{x}_1-{\mu }_1,x_2-{\mu }_2,\dots ,x_d-{\mu }_d\end{array}\right]\right] \\ \Rightarrow \Sigma =\left[\begin{array}{ccc}\mathbb{E}[(x_1-{\mu }_1{)}^2]& \mathbb{E}[(x1-\mu 1)(x2-\mu 2)]& ...\\ \mathbb{E}[(x2-\mu 2)(x1-\mu 1)]& \mathbb{E}[(x_2-{\mu }_2{)}^2]& ...\\ ⋮& ⋮& \ddots \end{array}\right] \\ 其中：\mathbb{E}[(x_1-{\mu }_1{)}^2]=\frac{1}{d}\sum _{k=1}^d({\mathbf{x}}_{k_{(i)}}-{\mu }_i{)}^2 \end{gathered}$$

• μ（mu） 是每个维度上的平均值；
• Σ（Sigma） 描述的是整个样本（或总体）中，各个维度之间的方差与相关性结构。

---

2. 关键步骤：把梯度搬进积分号

我们先写出边际密度
$$p(y)={\int }_{{\mathbb{R}}^d}p(y\mid x)p(x)dx.\text{\hspace{1em}(2.1)}$$

想要 ${\nabla }_{y}p(y)$，最直接是逐分量地对 $y_i$ 求偏导：
$$\frac{\partial }{\partial y_i}p(y)=\frac{\partial }{\partial y_i}\int p(y\mid x)p(x)dx.$$

结论（Leibniz 规则 / 主导收敛）
在常见的正则条件下（见下），可以交换“对 $y_i$ 的偏导”和“对 $x$ 的积分”：
$$\frac{\partial }{\partial y_i}p(y)=\int \frac{\partial }{\partial y_i}p(y\mid x)p(x)dx.\text{\hspace{1em}(2.2)}$$

把各分量重新打包回梯度向量，就得到
$${\nabla }_{y}p(y)=\int {\nabla }_{y}p(y\mid x)p(x)dx.\text{\hspace{1em}(2.3)}$$

什么时候合法？（足够条件）
对每个分量 $i$：

• $p(y\mid x)$ 关于 $y_i$ 处处可导；
• 存在某个与 $y$ 无关、可积的支配函数 $g_i(x)$，使得
  $|\partial p(y\mid x)/\partial y_i|\cdot p(x)\le g_i(x)$ 对所有 $y$ 成立；

则由主导收敛定理或Leibniz 积分求导法则，(2.2) 成立。
（高斯密度关于 (y) 光滑且衰减良好，通常满足这些条件。）

直观解释（非形式）:

因为 𝑝(𝑦∣𝑥) 对 𝑦 是一个平滑的钟形曲线，而且 𝑝(𝑥) 是固定的权重，所以当我们稍微改变 𝑦时，整个积分的变化等价于“每个 𝑥 对 𝑝(𝑦∣𝑥)”变化的加总”。

---

3. 先求 ${\nabla }_{y}p(y)$ 的表达式

由 (2.3)：
$${\nabla }_{y}p(y)=\int {\nabla }_{y}p(y\mid x)p(x)dx.\text{\hspace{1em}(3.1)}$$

再用“对数的梯度乘密度”技巧：
$${\nabla }_{y}p(y\mid x)=p(y\mid x){\nabla }_y\log p(y\mid x).\text{\hspace{1em}(3.2)}$$

首先我们知道
$$f(y)=e^{\log f(y)}$$
运用链式法则
$$\nabla f(y)=\nabla e^{\log f(y)}=e^{\log f(y)}\nabla \log f(y)=f(y)\nabla \log f(y)$$
直观理解：密度的相对变化率 = 对数密度的梯度。

• $\frac{dp}{dy}$：告诉你p(y)绝对值变化多块
• $\frac{d\log p}{dy}$：相对增长率，告诉你“p(y)在y方向上相对自己变化的速度”

代回 (3.1)：
$${\nabla }_{y}p(y)=\int p(y\mid x){\nabla }_y\log p(y\mid x)p(x)dx.\text{\hspace{1em}(3.3)}$$

两边同时除以 $p(y)$（假设 $p(y)>0$）得到 score：
$${\nabla }_y\log p(y)=\frac{1}{p(y)}\int p(y\mid x){\nabla }_y\log p(y\mid x)p(x)dx.\text{\hspace{1em}(3.4)}$$

---

4. 计算高斯似然的梯度 ${\nabla }_y\log p(y\mid x)$

一维高斯函数
$$f(x)=\frac{1}{\sqrt{2\pi }\sigma }\exp \left(-\frac{(x-\mu {)}^2}{2{\sigma }^2}\right)$$
当为标准正态分布时，函数为
$$f(x)=\frac{1}{\sqrt{2\pi }}\exp \left(-\frac{1}{2}{x}^2\right)$$
标准高维高斯分布函数，$z=(z_1,...,z_d{)}^T$
$$f(z)=\frac{1}{(2\pi {)}^{d/2}}\exp (-\frac{1}{2}\sum _{i=1}^d{z}_i^2)$$
通过将标准高斯分布进行线性变换和平移 $\mathbf{x}=\mu +Lz\Rightarrow z=L^{-1}(\mathbf{x}-\mu )$。
将$z=L^{-1}(\mathbf{x}-\mu )$带入标准高斯分布函数得到如下，其中$\Sigma =L{L}^T$
$$p(\mathbf{x}|\mu ,\Sigma )=\frac{1}{(2\pi {)}^{d/2}|\mathbf{\Sigma }{|}^{1/2}}\exp \left(-\frac{1}{2}(\mathbf{x}-\mu {)}^{\top }{\mathbf{\Sigma }}^{-1}(\mathbf{x}-\mu )\right)$$
$\Sigma$ 将一个高维球经过旋转和缩放变成了一个高维椭球分布，$\mu$将其进行平移

高斯似然：$y$ 已知，求 $\mathcal{N}(x,\Sigma )$
$$p(y\mid x)=\frac{1}{(2\pi {)}^{d/2}|\Sigma {|}^{1/2}}\exp (-\frac{1}{2}(y-x{)}^{\top }{\Sigma }^{-1}(y-x)).$$
取对数：
$$\log p(y\mid x)=\text{const}-\frac{1}{2}(y-x{)}^{\top }{\Sigma }^{-1}(y-x).$$
对 $y$ 求梯度（用二次型求导公式）：
$${\nabla }_y\log p(y\mid x)=-{\Sigma }^{-1}(y-x).\text{\hspace{1em}(4.1)}$$

把 (4.1) 代入 (3.4)：
$$\begin{gathered} {\nabla }_y\log p(y)=\frac{1}{p(y)}\int p(y\mid x)[-{\Sigma }^{-1}(y-x)]p(x)dx \\ =-{\Sigma }^{-1}\frac{1}{p(y)}\int (y-x)p(y\mid x)p(x)dx.\text{\hspace{1em}(4.2)} \end{gathered}$$

---

5. 用后验 $p(x\mid y)$ 化简

Bayes 定义：$p(x\mid y)=\frac{p(y\mid x)p(x)}{p(y)}$。
把它带入 (4.2)：
$${\nabla }_y\log p(y)=-{\Sigma }^{-1}\int (y-x)p(x\mid y),dx.\text{\hspace{1em}(5.1)}$$

把 (y) 拆出去（它不依赖 (x)）：
$$\begin{gathered} \int (y-x)p(x\mid y)dx \\ =y\int p(x\mid y)dx-\int xp(x\mid y)dx \\ =y-\mathbb{E}[x\mid y].\text{\hspace{1em}(5.2)} \end{gathered}$$

$p(x|y)$：在观察到 𝑦 后，𝑥 的概率权重
$$\int p(x|y)dx=1$$

• 在给定 𝑦 的条件下，所有可能的 𝑥 的概率总和为 1

$\int xp(x|y)dx=\mathbb{E}[x|y]$：加权平均后最可能的 $x\to$ 即 $\mathbb{E}[x|y]$

代回 (5.1)：
$${\nabla }_y\log p(y)=-{\Sigma }^{-1}(y-\mathbb{E}[x\mid y]).\text{\hspace{1em}(5.3)}$$

逐分量（索引）写法，便于核对

记 $[\cdot ]\ast i$ 表示向量的第 $i$ 个分量，${\Sigma }^{-1}=[{\Sigma }^{-1}]\ast ij$。
由 (5.3)：
$$\frac{\partial }{\partial y_i}\log p(y)=-\sum _{j=1}^d[{\Sigma }^{-1}{]}_{ij}(y_j-\mathbb{E}[x_j\mid y]).$$

---

6. 得到 Tweedie 公式（一般协方差）

把 (5.3) 左右同乘 $\Sigma$ 并移项：
$$\boxed{\mathbb{E}[x\mid y]=y+\Sigma {\nabla }_y\log p(y)}.\text{\hspace{1em}(6.1)}$$

形状检查（避免符号错误）：

• ${\nabla }_y\log p(y)\in {\mathbb{R}}^d$；
• $\Sigma \in {\mathbb{R}}^{d\times d}$；
• $\Sigma {\nabla }_y\log p(y)\in {\mathbb{R}}^d$，与 $y$ 同维。

---

7. 各向同性特例（最常见）

若 $\Sigma ={\sigma }^{2}I$：
$$\boxed{\mathbb{E}[x\mid y]=y+{\sigma }^2{\nabla }_y\log p(y)}.\text{\hspace{1em}(7.1)}$$

---

8. 小结（每一步做了什么 & 为什么合法）

1. 写边际：$p(y)=\int p(y\mid x)p(x)dx$（定义）。

2. 把梯度搬进积分号：${\nabla }_{y}p(y)=\int {\nabla }_{y}p(y\mid x)p(x)dx$。

   • 依据：Leibniz 规则 / 主导收敛（高斯情形满足光滑与支配条件）。

3. 换成“对数梯度 × 密度”：${\nabla }_{y}p(y\mid x)=p(y\mid x){\nabla }_y\log p(y\mid x)$（链式法则）。

4. 高斯对数梯度：${\nabla }_y\log p(y\mid x)=-{\Sigma }^{-1}(y-x)$（二次型求导）。

5. Bayes 化简：把 $\frac{p(y\mid x)p(x)}{p(y)}$ 认作 $p(x\mid y)$，并用 $\int p(x\mid y)dx=1$。

6. 移项得结论：$\mathbb{E}[x\mid y]=y+\Sigma {\nabla }_y\log p(y)$。

---

9. 直觉回顾（把公式读成一句话）

• $s(y):={\nabla }_y\log p(y)$ 指向密度更高的方向；
• $\Sigma s(y)$ 给出在噪声协方差尺度下的“回拉”位移；
• 把观测 $y$ 朝这个方向推回去，就得到最优去噪估计 $\mathbb{E}[x\mid y]$。