【P8815 [CSP-J 2022] 逻辑表达式】
题目:P8815 [CSP-J 2022] 逻辑表达式
题目描述
逻辑表达式是计算机科学中的重要概念和工具,包含逻辑值、逻辑运算、逻辑运算优先级等内容。
在一个逻辑表达式中,元素的值只有两种可能:000(表示假)和 111(表示真)。元素之间有多种可能的逻辑运算,本题中只需考虑如下两种:“与”(符号为 &)和“或”(符号为 |)。其运算规则如下:
0&0=0&1=1&0=00 \mathbin{\&} 0 = 0 \mathbin{\&} 1 = 1 \mathbin{\&} 0 = 00&0=0&1=1&0=0,1&1=11 \mathbin{\&} 1 = 11&1=1;
0∣0=00 \mathbin{|} 0 = 00∣0=0,0∣1=1∣0=1∣1=10 \mathbin{|} 1 = 1 \mathbin{|} 0 = 1 \mathbin{|} 1 = 10∣1=1∣0=1∣1=1。
在一个逻辑表达式中还可能有括号。规定在运算时,括号内的部分先运算;两种运算并列时,& 运算优先于 | 运算;同种运算并列时,从左向右运算。
比如,表达式 0|1&0 的运算顺序等同于 0|(1&0);表达式 0&1&0|1 的运算顺序等同于 ((0&1)&0)|1。
此外,在 C++ 等语言的有些编译器中,对逻辑表达式的计算会采用一种“短路”的策略:在形如 a&b 的逻辑表达式中,会先计算 a 部分的值,如果 a=0a = 0a=0,那么整个逻辑表达式的值就一定为 000,故无需再计算 b 部分的值;同理,在形如 a|b 的逻辑表达式中,会先计算 a 部分的值,如果 a=1a = 1a=1,那么整个逻辑表达式的值就一定为 111,无需再计算 b 部分的值。
现在给你一个逻辑表达式,你需要计算出它的值,并且统计出在计算过程中,两种类型的“短路”各出现了多少次。需要注意的是,如果某处“短路”包含在更外层被“短路”的部分内则不被统计,如表达式 1|(0&1) 中,尽管 0&1 是一处“短路”,但由于外层的 1|(0&1) 本身就是一处“短路”,无需再计算 0&1 部分的值,因此不应当把这里的 0&1 计入一处“短路”。
输入格式
输入共一行,一个非空字符串 sss 表示待计算的逻辑表达式。
输出格式
输出共两行,第一行输出一个字符 0 或 1,表示这个逻辑表达式的值;第二行输出两个非负整数,分别表示计算上述逻辑表达式的过程中,形如 a&b 和 a|b 的“短路”各出现了多少次。
输入输出样例 #1
输入 #1
0&(1|0)|(1|1|1&0)
输出 #1
1
1 2
输入输出样例 #2
输入 #2
(0|1&0|1|1|(1|1))&(0&1&(1|0)|0|1|0)&0
输出 #2
0
2 3
说明/提示
【样例解释 #1】
该逻辑表达式的计算过程如下,每一行的注释表示上一行计算的过程:
0&(1|0)|(1|1|1&0)
=(0&(1|0))|((1|1)|(1&0)) //用括号标明计算顺序
=0|((1|1)|(1&0)) //先计算最左侧的 &,是一次形如 a&b 的“短路”
=0|(1|(1&0)) //再计算中间的 |,是一次形如 a|b 的“短路”
=0|1 //再计算中间的 |,是一次形如 a|b 的“短路”
=1
【样例 #3】
见附件中的 expr/expr3.in 与 expr/expr3.ans。
【样例 #4】
见附件中的 expr/expr4.in 与 expr/expr4.ans。
【数据范围】
设 ∣s∣\lvert s \rvert∣s∣ 为字符串 sss 的长度。
对于所有数据,1≤∣s∣≤1061 \le \lvert s \rvert \le {10}^61≤∣s∣≤106。保证 sss 中仅含有字符 0、1、&、|、(、) 且是一个符合规范的逻辑表达式。保证输入字符串的开头、中间和结尾均无额外的空格。保证 sss 中没有重复的括号嵌套(即没有形如 ((a)) 形式的子串,其中 a 是符合规范的逻辑表达式)。
| 测试点编号 | ∣s∣≤\lvert s \rvert \le∣s∣≤ | 特殊条件 |
|---|---|---|
| 1∼21 \sim 21∼2 | 333 | 无 |
| 3∼43 \sim 43∼4 | 555 | 无 |
| 555 | 200020002000 | 1 |
| 666 | 200020002000 | 2 |
| 777 | 200020002000 | 3 |
| 8∼108 \sim 108∼10 | 200020002000 | 无 |
| 11∼1211 \sim 1211∼12 | 106{10}^6106 | 1 |
| 13∼1413 \sim 1413∼14 | 106{10}^6106 | 2 |
| 15∼1715 \sim 1715∼17 | 106{10}^6106 | 3 |
| 18∼2018 \sim 2018∼20 | 106{10}^6106 | 无 |
其中:
特殊性质 1 为:保证 sss 中没有字符 &。
特殊性质 2 为:保证 sss 中没有字符 |。
特殊性质 3 为:保证 sss 中没有字符 ( 和 )。
【提示】
以下给出一个“符合规范的逻辑表达式”的形式化定义:
- 字符串
0和1是符合规范的; - 如果字符串
s是符合规范的,且s不是形如(t)的字符串(其中t是符合规范的),那么字符串(s)也是符合规范的; - 如果字符串
a和b均是符合规范的,那么字符串a&b、a|b均是符合规范的; - 所有符合规范的逻辑表达式均可由以上方法生成。
理解
经过对数据的推演,大量反思总结出生成二叉树的规则
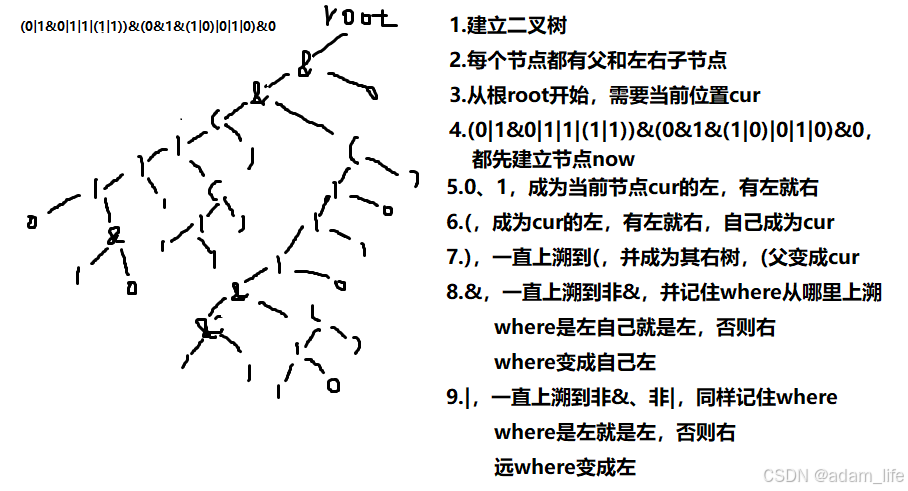
1.建立二叉树
2.每个节点都有父和左右子节点
3.从根root开始,需要当前位置cur
4.(0|1&0|1|1|(1|1))&(0&1&(1|0)|0|1|0)&0
都先建立节点now
5.0、1
成为当前节点cur的左,有左就右
6.(
成为cur的左,有左就右
自己成为cur
7.)
一直上溯到(,并成为其右树,
(父变成cur
8.&
一直上溯到非&,并记住where从哪里上溯
where是左自己就是左,否则右
where变成自己左
9.|
一直上溯到非&、非|,同样记住where
where是左就是左,否则右
远where变成左
代码
#include <bits/stdc++.h>
using namespace std;
struct node{//二叉树节点 char c;//运算符bool k;//布尔值node *f,*l,*r;//父节点,左右子节点node(){c='*',f=l=r=NULL;} //无参构造 node(char x){c=x,f=l=r=NULL,k=(c=='1');}//有参构造
}root;//二叉树根
void add(node *f,node *c){//子节点c挂到f的左,有左就右 c->f=f;if(!f->l)f->l=c;else f->r=c;
}
void view(node *x){//后序遍历,逆波兰表达式,天然有序,无需考虑优先级 if(x->l)view(x->l);if(x->r)view(x->r);if(x->c!='('||x->c!=')')cout<<x->c;
}
string s;//输入的运算符
bool ans;//逻辑运算结果
int he_and=0,he_or=0;//从左运算,“短路”的数量
bool go(node *x){//从根开始运算 if(x->c=='0'||x->c=='1')return x->c=='1';//直接返回0、1 bool k1,k2;//左右分支的运算结果 if(x->l)k1=go(x->l);//有左就算左 if(x->c=='|'&&k1==1){he_or++;return 1;}//或短路 if(x->c=='&'&&k1==0){he_and++;return 0;}//与短路 if(x->c!='('&&x->r)k2=go(x->r);//无短路就算右分支 if(x->c=='|')return k1||k2;//或运算 else if(x->c=='&')return k1&&k2;//与运算 else if(x->c=='('||x->c=='*')return k1;//单分支
}
int main(){//freopen("data.cpp","r",stdin);node *cur=&root;//开始时根就是当前节点,一直记住当前节点 cin>>s;//优先级高潜里,否则浮上(0|1&0|1|1|(1|1))&(0&1&(1|0)|0|1|0)&0 for(int i=0;i<s.length();i++){//遍历每个字符 node *now=new node(s[i]);//每个字符都建立节点,对应现在指针 if(s[i]=='('){add(cur,now);cur=now;}//挂到当前节点,后自己时当前节点 else if(s[i]==')'){while(cur->c!='(')cur=cur->f;//上浮,一直找到(父 add(cur,now);cur=cur->f;//挂到当前节点,收括号后上浮一层 }else if(s[i]=='&'){node *child;//确定上浮自左右哪个分支 if(cur->r)child=cur->r;//有有节点就是右 else child=cur->l;//否则就是左 while(cur->c=='&')child=cur,cur=cur->f;//只比&优先级低,唯遇到&上浮 now->f=cur;//挂当前节点 if(cur->l==child)cur->l=now;//替代child的分支,就是挂当前节点的左右哪个 else cur->r=now;add(now,child);cur=now;//把原先的child挂到自己左节点 }else if(s[i]=='|'){node *child;if(cur->r)child=cur->r;else child=cur->l;while(cur->c=='&'||cur->c=='|')child=cur,cur=cur->f;//只比|和&优先级低 now->f=cur;if(cur->l==child)cur->l=now;else cur->r=now;add(now,child);cur=now;}else add(cur,now);//加0、1数值 }//view(&root); cout<<endl;ans=go(&root);//运算,并统计“短路”数 cout<<ans<<"\n"<<he_and<<" "<<he_or; return 0;
}
时间复杂度
1.建树过程中,每个字符执行一次节点创建、指针调整等操作,单次是O(1),所以总复杂度是O(n)。
2.递归函数(完成逻辑运算)也是恰好遍历一次每个节点,所以复杂度也是O(n)。
