凹凸性-信息论
Jensen’s inequality

注释:函数值的平权大于函数点的平均
Non-negativity of KL-Distance
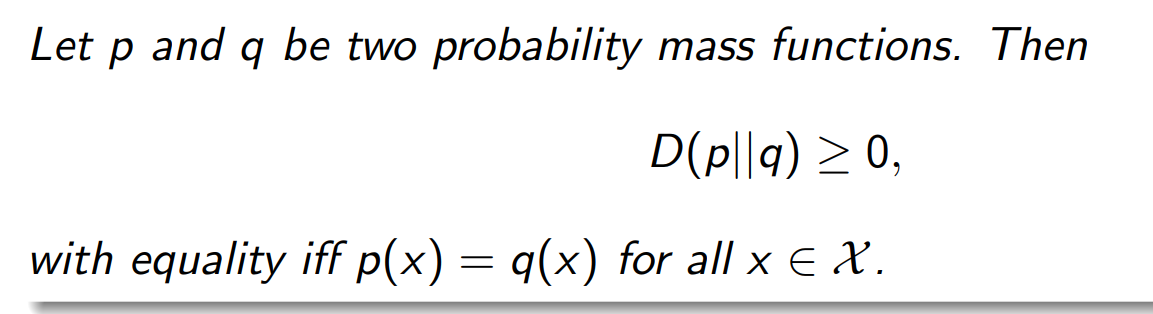
Maximum Entropy Theorem最大熵定理
H(X)≤log(∣X∣)H(X) ≤ log(|X|)H(X)≤log(∣X∣)
用KL-distance 非负性推出
KL 散度总是非负:
DKL(P∥U)=∑xP(x)logP(x)1/n≥0D_{KL}(P \| U) = \sum_x P(x) \log \frac{P(x)}{1/n} \geq 0DKL(P∥U)=x∑P(x)log1/nP(x)≥0
展开:
DKL(P∥U)=∑xP(x)logP(x)+∑xP(x)lognD_{KL}(P \| U) = \sum_x P(x) \log P(x) + \sum_x P(x)\log nDKL(P∥U)=x∑P(x)logP(x)+x∑P(x)logn
注意 ∑xP(x)=1\sum_x P(x)=1∑xP(x)=1,所以:
DKL(P∥U)=−H(X)+lognD_{KL}(P \| U) = -H(X) + \log nDKL(P∥U)=−H(X)+logn
因此:
−H(X)+logn≥0⇒H(X)≤logn.-H(X) + \log n \ge 0 \quad \Rightarrow \quad H(X) \le \log n.−H(X)+logn≥0⇒H(X)≤logn.
等号条件
当 P=U即 X 服从均匀分布时),KL 散度为零,上界取到:
H(X)=log∣X∣H(X) = \log |\mathcal{X}|H(X)=log∣X∣
严格凹函数 ⇒ 极值唯一
我们已经知道
H(P)=−∑i=1npilogpiH(P) = -\sum_{i=1}^n p_i \log p_iH(P)=−i=1∑npilogpi
是 严格凹函数(因为每个项 −pilogpi-p_i \log p_i−pilogpi 的二阶导数为 −1/pi<0-1/p_i < 0−1/pi<0)。
对一个严格凹函数 f,若在凸约束集上(如概率单纯形)存在驻点,则该驻点是唯一的全局最大值。
换句话说:
严格凹+线性约束⟹唯一的最大点。
这里的 |X|代表什么
H(X)≤log∣X∣H(X) \le \log |X|H(X)≤log∣X∣
实际上这里的 ∣X∣ 是指 随机变量 X 能取的不同取值的数量,也就是它的样本空间的基数(cardinality)。
KL散度和互信息的区别:
| 层级 | KL 散度 | 互信息 |
|---|---|---|
| 样本空间 | 一维 (X)(\mathcal{X})(X) | 二维 (X×Y)(\mathcal{X}\times\mathcal{Y})(X×Y) |
| 比较对象 | 真实分布 vs 模型分布 | 真实联合分布 vs 假设独立分布 |
| 几何意义 | 衡量“两个分布的距离” | 衡量“真实相关性偏离独立的程度” |
| 信息含义 | 模型误差 | 变量间共享信息 |
Log sum inequality

f(平均)≤平均的ff(平均)≤平均的ff(平均)≤平均的f
Convexity of KL-distance

Convexity of Mutual Information(重点)
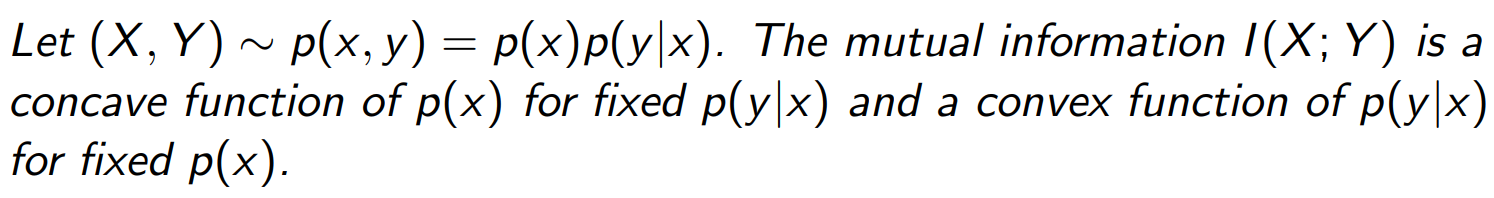
我们考虑一个随机变量对 (X, Y),它的联合分布由 边缘分布 p(x)(输入的分布)和 条件分布 p(y|x)(信道或传输规律)共同决定。
互信息 I(X; Y) 描述 X 与 Y 之间的信息量。 它对输入分布 p(x) 呈 凹函数(concave),对信道分布 p(y|x) 呈凸函数(convex)。
I(X;Y)=H(Y)−H(Y∣X) I(X;Y)=H(Y)−H(Y∣X)I(X;Y)=H(Y)−H(Y∣X)
H(Y)=∑yp(y)log1p(y),H(Y)=\sum_{y}p(y)\log\frac{1}{p(y)},H(Y)=y∑p(y)logp(y)1,p(y)=∑xp(x)p(y∣x)p(y)=\sum_{x}p(x)p(y∣x)p(y)=x∑p(x)p(y∣x)
H(Y∣X)=∑xp(x)H(Y∣X=x))=∑xp(x)∑yp(y∣x)log1p(y∣x)H(Y∣X)=\sum_{x}p(x)H(Y|X=x))=\sum_{x}p(x)\sum_{y}p(y∣x)log\frac{1}{p(y∣x)}H(Y∣X)=x∑p(x)H(Y∣X=x))=x∑p(x)y∑p(y∣x)logp(y∣x)1
总结凹凸性:
| 函数 | 依赖变量 | 凹/凸性质 | 原因 |
|---|---|---|---|
| H(p)H(p)H(p) | p(x)p(x)p(x) | 凹(concave) | 混合增加不确定性混合增加不确定性混合增加不确定性 |
| D(p‖q)D(p‖q)D(p‖q) | (p,q)(p,q)(p,q) | 联合 凸(convex) | KL散度的凸性定理KL散度的凸性定理KL散度的凸性定理 |
| I(X;Y)=D(p(x,y)‖p(x)p(y))I(X;Y)=D(p(x,y)‖p(x)p(y))I(X;Y)=D(p(x,y)‖p(x)p(y)) | p(x)凹;p(y∣x)凸p(x)凹; p(y|x) 凸p(x)凹;p(y∣x)凸 | 从KL的联合凸性与线性映射推导从KL的联合凸性与线性映射推导从KL的联合凸性与线性映射推导 |
Markov chain
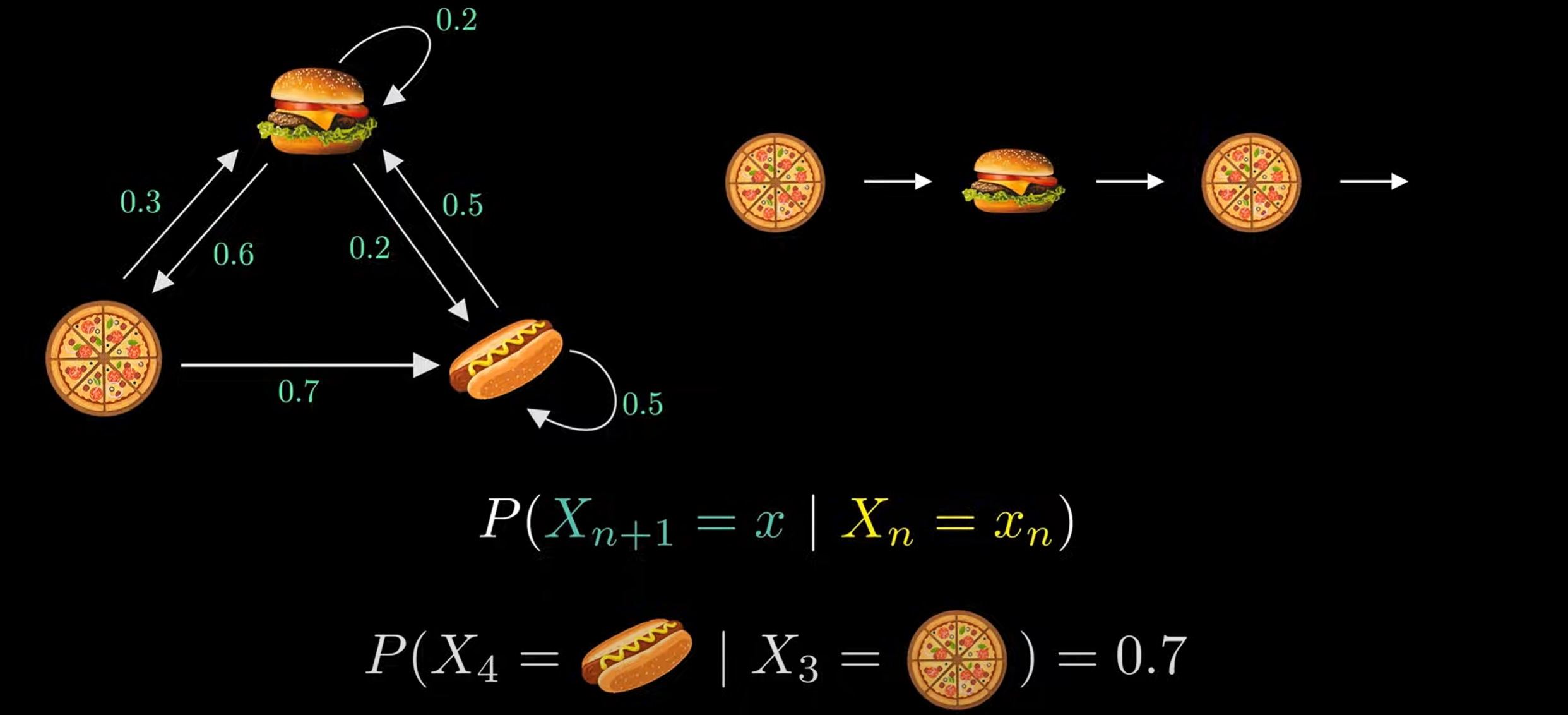
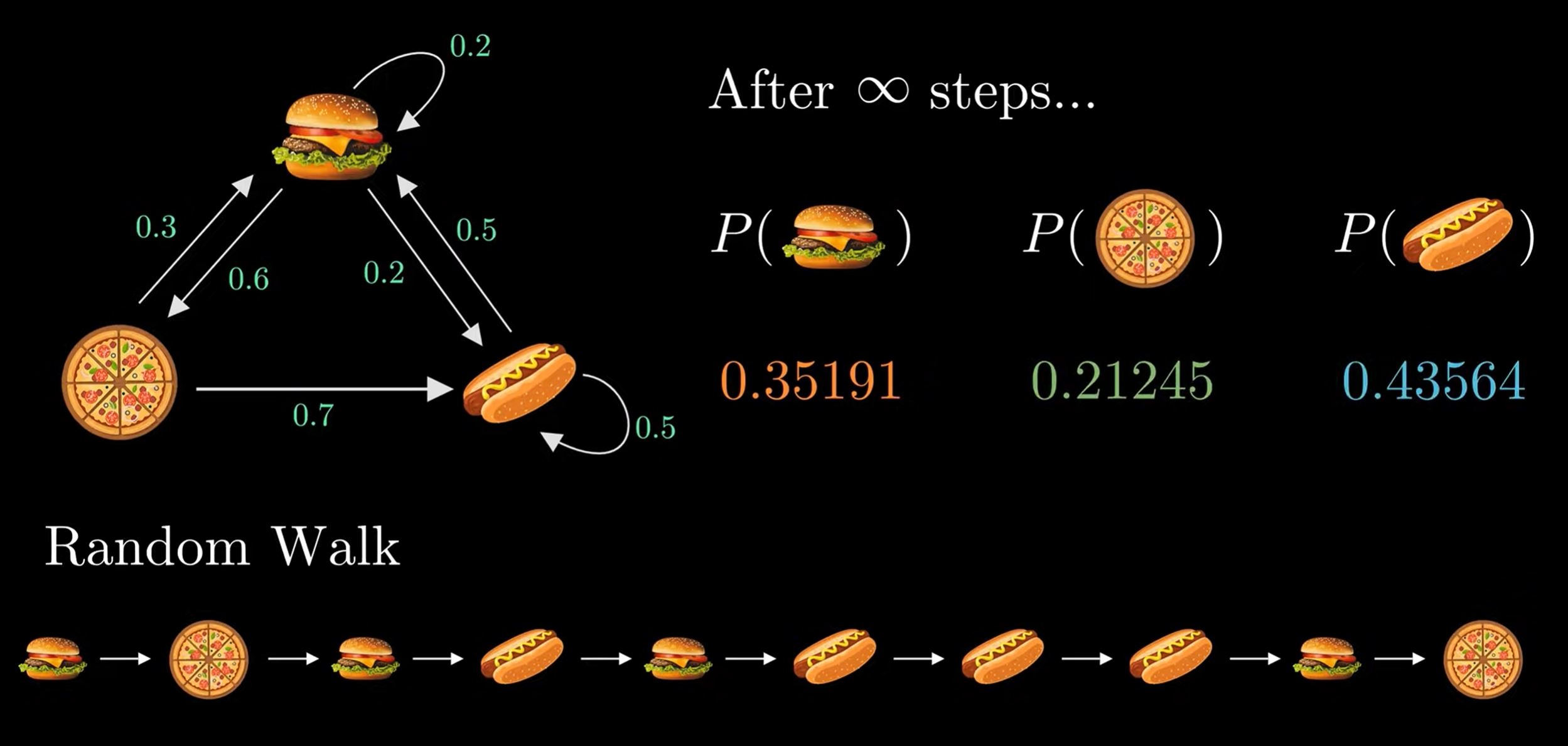
Data Processing Inequality

注意:
-
I(X;Y)I(X;Y)I(X;Y):两个圆重叠的部分。
-
I(X;Y,Z)I(X;Y,Z)I(X;Y,Z):X 的圆与 Y,Z 联合的圆的交叠面积(整个Y∪ZY\cup ZY∪Z 区域和XXX的交集)。
-
I(X;Y;Z)I(X;Y;Z)I(X;Y;Z):是三者交叠的中间那一块重叠部分(即三圆交集区域)。
I(X;Y,Z)=I(X;Z)+I(X;Y∣Z)=I(X;Y)+I(X;Z∣Y).I(X; Y , Z) = I(X; Z) + I(X; Y |Z) = I(X; Y ) + I(X; Z|Y ). I(X;Y,Z)=I(X;Z)+I(X;Y∣Z)=I(X;Y)+I(X;Z∣Y).
As I(X;Z∣Y)=0,then I(X;Y)≥I(X;Z).As \ I(X; Z|Y ) = 0, then \ I(X; Y ) ≥ I(X; Z).As I(X;Z∣Y)=0,then I(X;Y)≥I(X;Z).
这种叫conditional independent :
未知 YYY的时候X,ZX,ZX,Z不独立
已知YYY的时候X,ZX,ZX,Z独立
Sufficient Statistics

| 步骤 | 含义 |
|---|---|
| Given: | XXX来自参数化分布 fθ(x)f_\theta(x)fθ(x),且定义了统计量T(X)T(X)T(X)。 |
| Assume / Check: | 给定 T(X)T(X)T(X)后,XXX与 θ\thetaθ条件独立。 |
| Then: | 我们称 T(X) 是参数 θ\thetaθ 的充分统计量。 |
① 生成过程(自然的信息流方向)
在统计建模里,样本的生成顺序确实是:
θ⟶X⟶T(X)θ⟶X⟶T(X)θ⟶X⟶T(X)
也就是说:
-
θ 是分布的参数,先确定它;
-
然后根据 fθ(x)f_\theta(x)fθ(x) 从这个分布中采样出数据 XXX;
-
最后我们从样本中计算出一个统计量 T(X)T(X)T(X)。
这就是生成模型的自然方向。
② 充分统计量定义时的条件独立方向
但是,当我们定义“充分统计量”时,我们要求:
X 与 θ 条件独立,给定 T(X)
也就是:
P(X∣θ,T(X))=P(X∣T(X))P(X|\theta, T(X)) = P(X|T(X))P(X∣θ,T(X))=P(X∣T(X))
I(θ;X∣T(X))=0I(θ;X∣T(X))=0I(θ;X∣T(X))=0
这个条件反过来可以写成一条 Markov 链:
θ⟶T(X)⟶Xθ⟶T(X)⟶Xθ⟶T(X)⟶X
意思是:
一旦我们知道了 T(X)T(X)T(X),参数 θ 对 X 就不再有直接影响了(信息流被 T(X)T(X)T(X) 截断了)。
Shannon’s Source Coding Theorem

Coding Theorem for DMS

| 特性 | 定长编码 | 变长编码 |
|---|---|---|
| 码字长度 | 全部相同 | 根据符号频率不同而变化 |
| 示例 | A=00, B=01, C=10, D=11 | A=0, B=10, C=110, D=111 |
| 优点 | 编码/解码简单、易同步 | 能根据概率分配更短码,节省平均码长 |
| 缺点 | 不够压缩高效 | 需要设计前缀码、防止歧义 |
| 应用 | 固定块压缩、信道编码 | Huffman 编码、算术编码、自然语言压缩 |
在源编码定理里,n 是“块长”(block length),也就是我们一次拿多少个源符号一起去编码。
现实里,信息源 X 会持续输出很多符号:
X1,X2,X3,X4,…X_1, X_2, X_3, X_4, \dotsX1,X2,X3,X4,…
比如:
-
X1X_1X1 = 第一个字母
-
X2X_2X2 = 第二个字母
-
X3X_3X3 = 第三个字母
我们可以选择“每次编码 1 个符号”,也可以选择“每次编码 2 个、4 个、1000 个符号”, 这时的“每次编码的符号数量”就是 n。
RnR_{n}Rn就是这“一次性编码 n 个符号”方案的平均码率(average rate per source symbol)。 它表示:在这个块长为 n 的编码器下,每个源符号平均用了多少比特去描述。n 越大,Rₙ 越接近 H(X)。
R 是你允许的“平均码率上限”;
typical set

性质
典型集的这些性质(信息量差不多、概率差不多、总概率≈1)只有当 n 很大时才成立。

编码

