怎么做淘宝返利网站wordpress打印文章

前言：这是专门针对java语言讲解的算法解析（题目顺序大致参考《代码随想录》）

思维导图

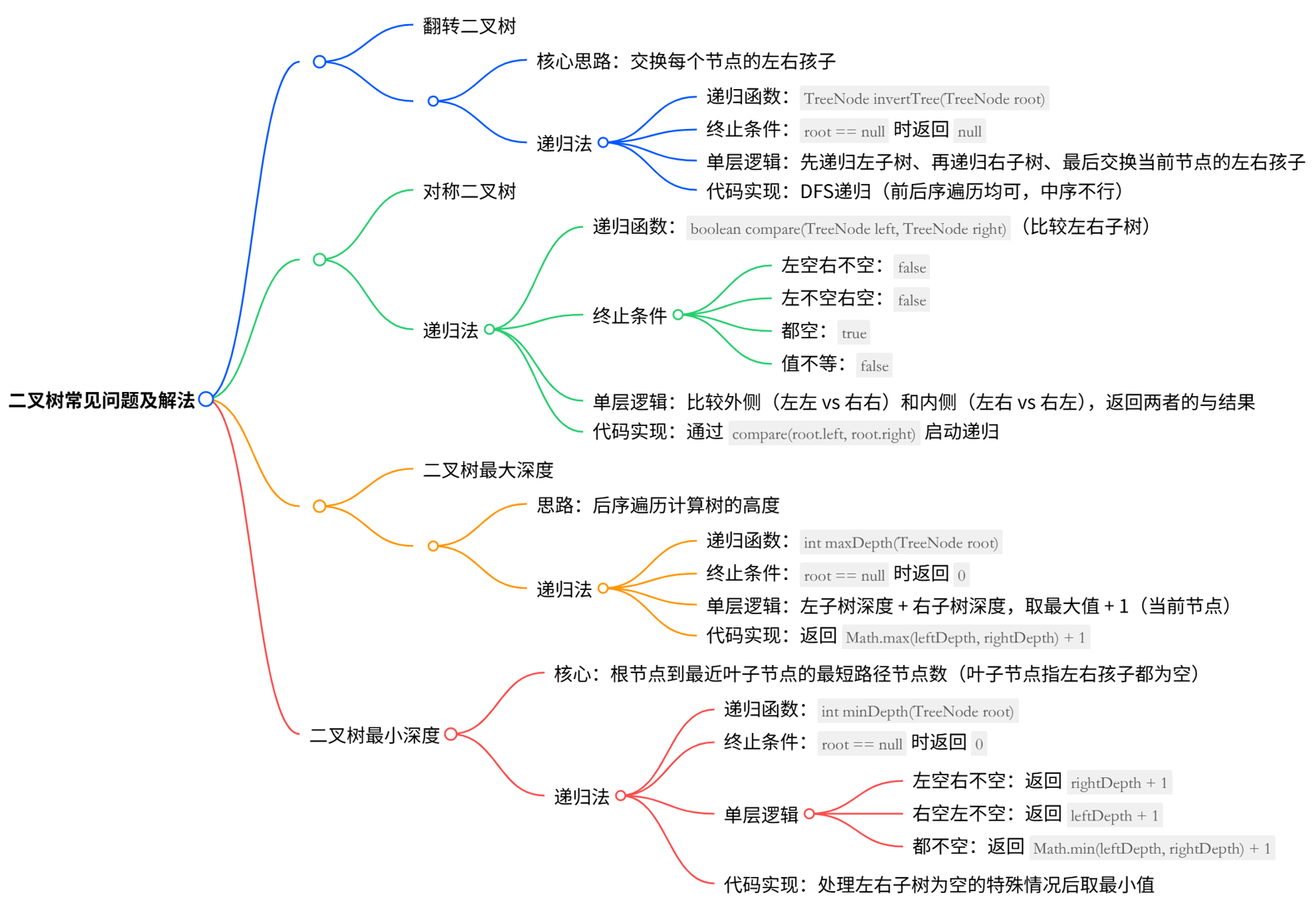
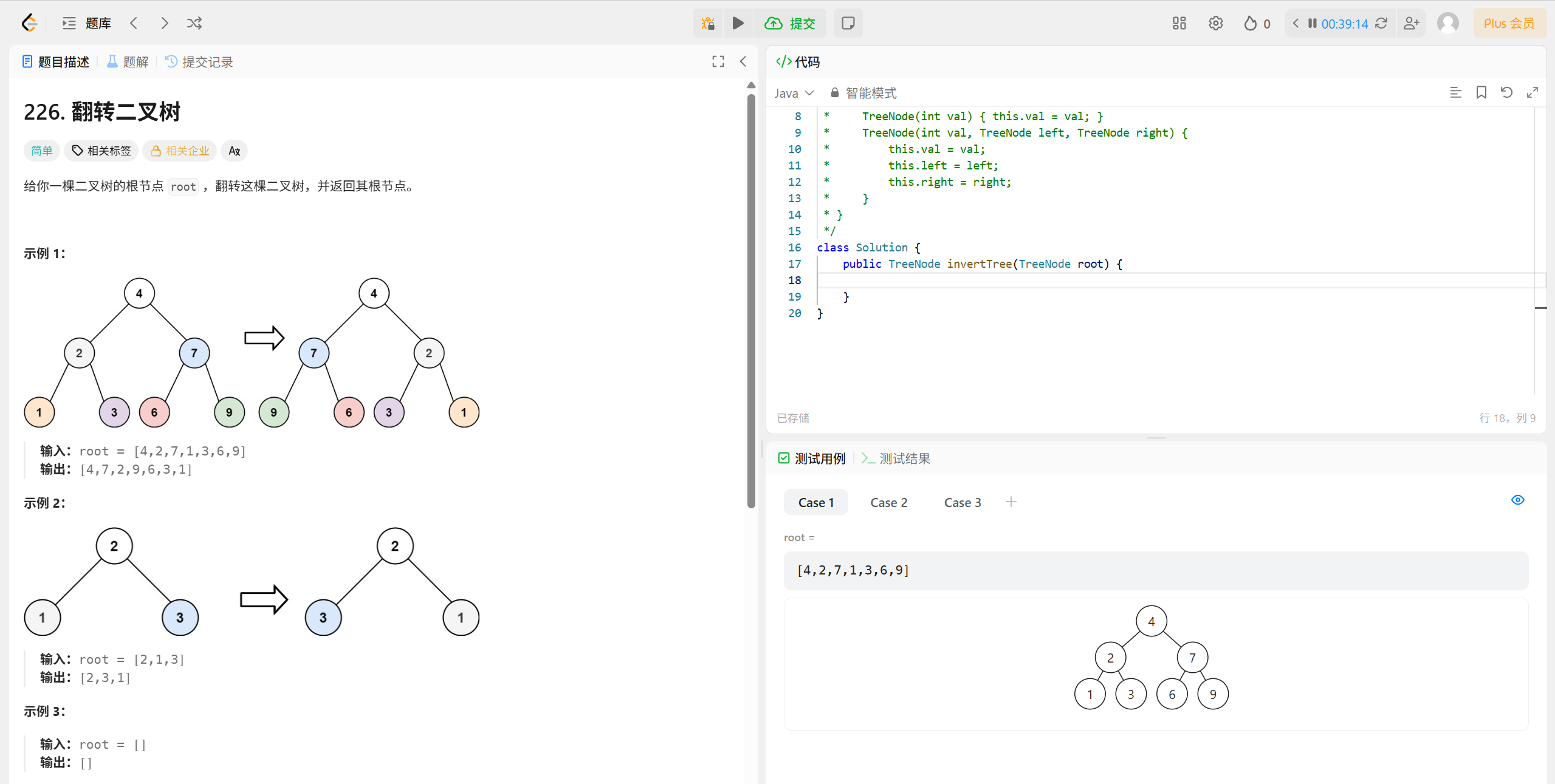
226. 翻转二叉树

---

思路

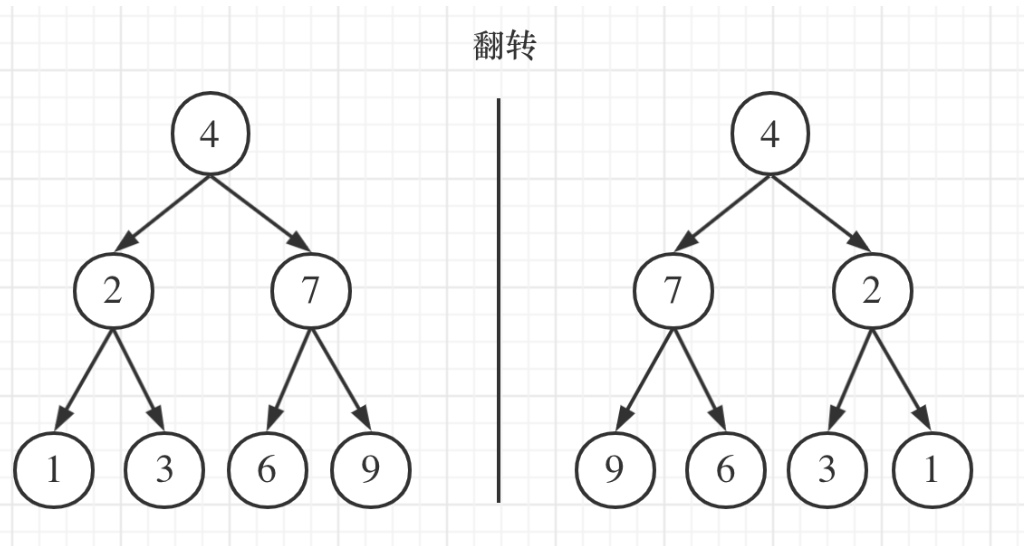
可以发现想要翻转它，其实就把每一个节点的左右孩子交换一下就可以了。

递归法

我们下文以前序遍历为例，通过动画来看一下翻转的过程:

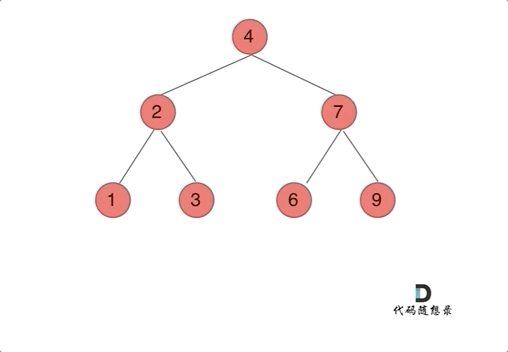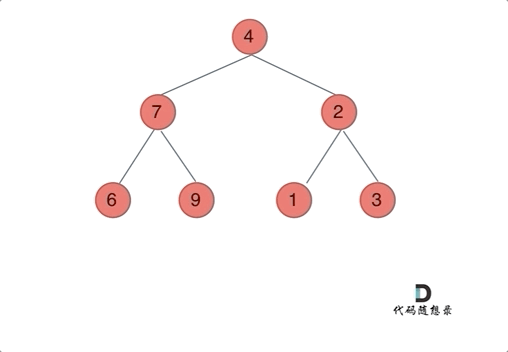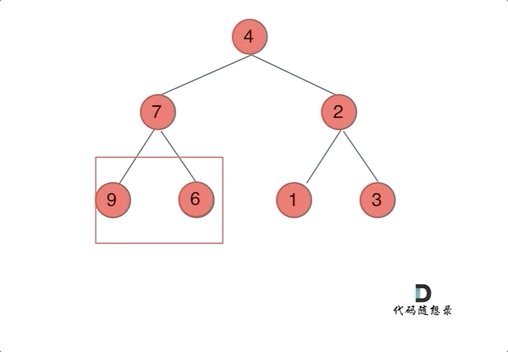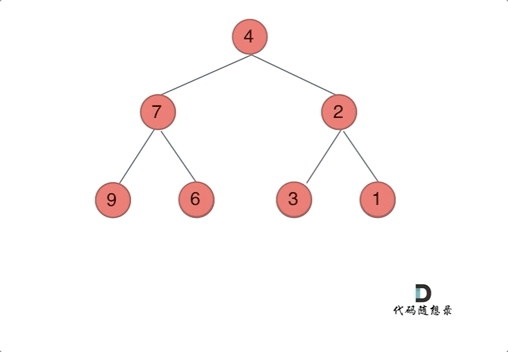
递归三部曲：

1. 确定递归函数的参数和返回值

参数就是要传入节点的指针，不需要其他参数了，通常此时定下来主要参数，如果在写递归的逻辑中发现还需要其他参数的时候，随时补充。

TreeNode invertTree(TreeNode root)；

2. 确定终止条件

当前节点为空的时候，就返回

 if (root == null) {return null;}

3. 确定单层递归的逻辑

因为是前序遍历，所以先进行交换左右孩子节点，然后反转左子树，反转右子树。

invertTree(root.left);
invertTree(root.right);
swapChildren(root);private void swapChildren(TreeNode root) {TreeNode tmp = root.left;root.left = root.right;root.right = tmp;}

代码实现：

//DFS递归
class Solution {/*** 前后序遍历都可以* 中序不行，因为先左孩子交换孩子，再根交换孩子（做完后，右孩子已经变成了原来的左孩子），再右孩子交换孩子（此时其实是对原来的左孩子做交换）*/public TreeNode invertTree(TreeNode root) {if (root == null) {return null;}invertTree(root.left);invertTree(root.right);swapChildren(root);return root;}private void swapChildren(TreeNode root) {TreeNode tmp = root.left;root.left = root.right;root.right = tmp;}
}

101. 对称二叉树

---

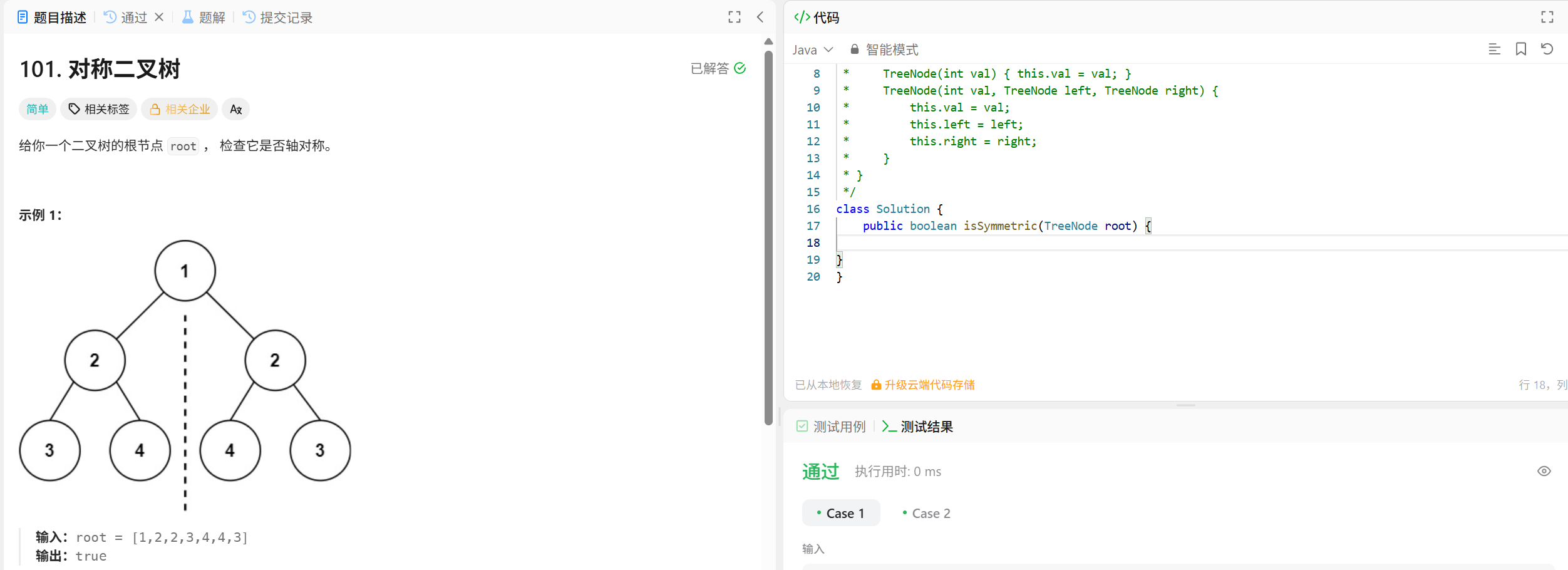
递归法

1.确定递归函数的参数和返回值

因为我们要比较的是根节点的两个子树是否是相互翻转的，进而判断这个树是不是对称树，所以要比较的是两个树，参数自然也是左子树节点和右子树节点。

boolean compare(TreeNode left, TreeNode right)

2.确定终止条件

首先要把两个节点为空的情况弄清楚，避免比较数值的时候出现空指针异常。

节点为空的情况有：（注意我们比较的其实不是左孩子和右孩子，所以如下我称之为左节点右节点）

• 左节点为空，右节点不为空，不对称，return false
• 左不为空，右为空，不对称 return false
• 左右都为空，对称，返回true

此时已经排除掉了节点为空的情况，那么剩下的就是左右节点不为空：

• 左右都不为空，比较节点数值，不相同就return false

此时左右节点不为空，且数值也不相同的情况我们也处理了。

        if (left == null && right == null) {return true;}if (left == null && right != null) {return false;}if (left != null && right == null) {return false;}if (left.val != right.val) {return false;}

注意上面最后一种情况，我没有使用else，而是else if， 因为我们把以上情况都排除之后，剩下的就是 左右节点都不为空，且数值相同的情况。

3.确定单层递归的逻辑

此时才进入单层递归的逻辑，单层递归的逻辑就是处理 左右节点都不为空，且数值相同的情况。

• 比较二叉树外侧是否对称：传入的是左节点的左孩子，右节点的右孩子。
• 比较内侧是否对称，传入左节点的右孩子，右节点的左孩子。
• 如果左右都对称就返回true ，有一侧不对称就返回false 。

        boolean outer = compare(left.left, right.right);boolean inner = compare(left.right, right.left);boolean res = outer && inner;return res;

代码实现：

 /*** 递归法*/public boolean isSymmetric1(TreeNode root) {return compare(root.left, root.right);}private boolean compare(TreeNode left, TreeNode right) {if (left == null && right != null) {return false;}if (left != null && right == null) {return false;}if (left == null && right == null) {return true;}if (left.val != right.val) {return false;}// 比较外侧boolean compareOutside = compare(left.left, right.right);// 比较内侧boolean compareInside = compare(left.right, right.left);return compareOutside && compareInside;}

104. 二叉树最大深度

---

思路

我先用后序遍历（左右中）来计算树的高度。

1.确定递归函数的参数和返回值：参数就是传入树的根节点，返回就返回这棵树的深度，所以返回值为int类型。

int getdepth(TreeNode node)

2.确定终止条件：如果为空节点的话，就返回0，表示高度为0。

if (node == NULL) return 0;

3.确定单层递归的逻辑：先求它的左子树的深度，再求右子树的深度，最后取左右深度最大的数值 再+1 （加1是因为算上当前中间节点）就是目前节点为根节点的树的深度。

int leftdepth = getdepth(node.left);       // 左
int rightdepth = getdepth(node.right);     // 右
int depth = 1 + max(leftdepth, rightdepth); // 中
return depth;

代码实现：

class Solution {/*** 递归法*/public int maxDepth(TreeNode root) {if (root == null) {return 0;}int leftDepth = maxDepth(root.left);int rightDepth = maxDepth(root.right);return Math.max(leftDepth, rightDepth) + 1;}
}

111. 二叉树最小深度

---

思路：

这道题直觉上好像和求最大深度差不多，其实还是差不少的。

本题依然是前序遍历和后序遍历都可以，前序求的是深度，后序求的是高度。

• 二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数或者节点数（取决于深度从0开始还是从1开始）
• 二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数或者节点数（取决于高度从0开始还是从1开始）

那么使用后序遍历，其实求的是根节点到叶子节点的最小距离，就是求高度的过程，不过这个最小距离 也同样是最小深度。

以下讲解中遍历顺序上依然采用后序遍历（因为要比较递归返回之后的结果，本文我也给出前序遍历的写法）。

本题还有一个误区，在处理节点的过程中，最大深度很容易理解，最小深度就不那么好理解

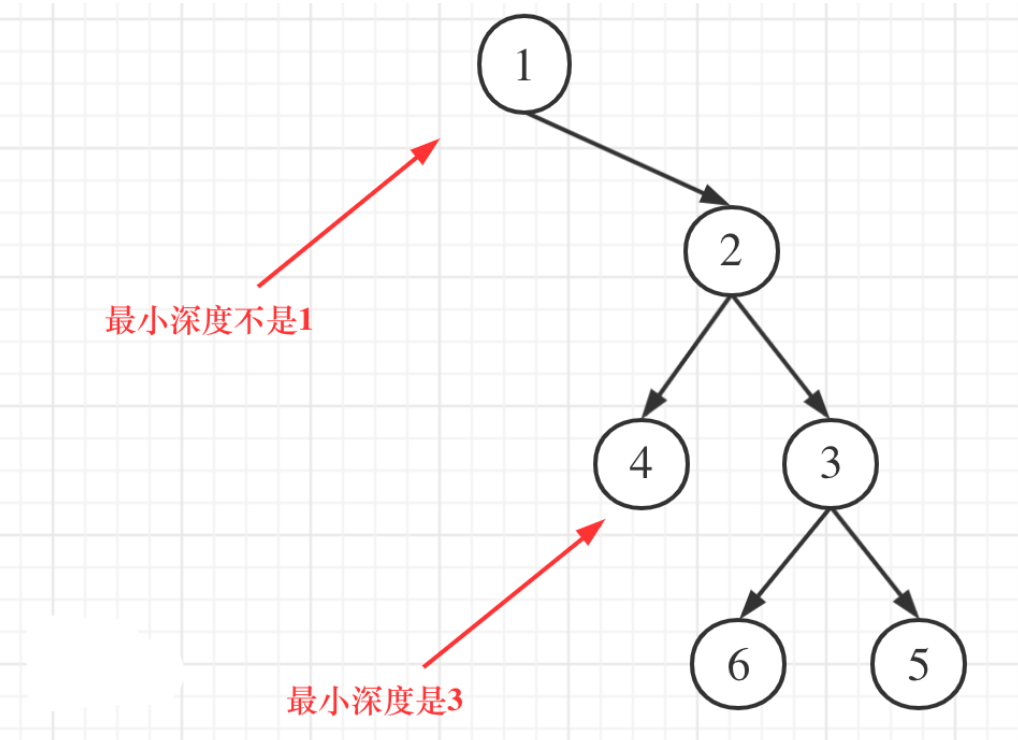
这就重新审题了，题目说的是：最小深度是从根节点到最近叶子节点的最短路径上的节点数量。注意是叶子节点。什么是叶子节点，左右孩子都为空的节点才是叶子节点！

递归法

1.确定递归函数的参数和返回值：参数为要传入的二叉树根节点，返回的是int类型的深度。

int getDepth(TreeNode* node)

2.确定终止条件：终止条件也是遇到空节点返回0，表示当前节点的高度为0。

if (node == NULL) return 0;

3.确定单层递归的逻辑：这块和求最大深度可就不一样了，一些同学可能会写如下代码：

int leftDepth = getDepth(node->left);
int rightDepth = getDepth(node->right);
int result = 1 + min(leftDepth, rightDepth);
return result;

这个代码就犯了此图中的误区：

如果这么求的话，没有左孩子的分支会算为最短深度。

所以，如果左子树为空，右子树不为空，说明最小深度是 1 + 右子树的深度。

反之，右子树为空，左子树不为空，最小深度是 1 + 左子树的深度。 最后如果左右子树都不为空，返回左右子树深度最小值 + 1 。

代码实现：

class Solution {/*** 递归法，相比求MaxDepth要复杂点* 因为最小深度是从根节点到最近**叶子节点**的最短路径上的节点数量*/public int minDepth(TreeNode root) {if (root == null) {return 0;}int leftDepth = minDepth(root.left);int rightDepth = minDepth(root.right);if (root.left == null) {return rightDepth + 1;}if (root.right == null) {return leftDepth + 1;}// 左右结点都不为nullreturn Math.min(leftDepth, rightDepth) + 1;}
}

---