刷题记录 动态规划-29,30,31 HOT100 动态规划-3 打家劫舍系列
题目:
198. 打家劫舍
213. 打家劫舍 II
337. 打家劫舍 III
母题:198. 打家劫舍
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
示例 1:
输入:[1,2,3,1] 输出:4 解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。 偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:
输入:[2,7,9,3,1] 输出:12 解释:偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。 偷窃到的最高金额 = 2 + 9 + 1 = 12 。
提示:
1 <= nums.length <= 1000 <= nums[i] <= 400
一、母题:打家劫舍
1.模式识别
当前房间偷不偷取决于上一个房间 》 当前状态取决于前面的状态 》 动态规划,当然打家劫舍本来就是经典动态规划题目
核心原理:当前状态 = max(打劫相邻房间, 不打劫相邻房间 + 当前房间金额)
2.母题代码实现
1.二维数组
维度1:房间
维度2:(打劫当前房间所得,不打劫当前房间所得)
即,当前状态 = max(上一个状态)
class Solution:
def rob(self, nums: List[int]) -> int:
n = len(nums)
dp = [[0] * 2 for _ in range(n + 1)]
for i, num in enumerate(nums):
dp[i + 1][0] = max(dp[(i + 1) - 1])
dp[i + 1][1] = dp[(i + 1) - 1][0] + num
return max(dp[-1])2.一维数组
当前状态 = max(上一个状态,上两个状态 + 当前节点值)
class Solution:
def rob(self, nums: List[int]) -> int:
n = len(nums)
dp = [0] * (n + 2)
for i, num in enumerate(nums):
dp[i + 2] = max(dp[(i - 2) + 2] + num, dp[(i - 1) + 2])
return dp[-1]3.O1空间版
由于一维数组存在较强的无后效性,本题可以连数组都省去
class Solution:
def rob(self, nums: List[int]) -> int:
n = len(nums)
prev1, prev2 = 0, 0
cur = 0
for num in nums:
# 计算当前
cur = max(prev1, prev2 + num)
# 时间流逝
prev1, prev2 = cur, prev1
return cur二、打家劫舍 + 循环数组
1.模式识别
当前状态 = max(打劫相邻房间, 不打劫相邻房间 + 当前房间金额)
对于类似数组这样的线性数据结构,可以通过分情况讨论来处理,
这里借用代码随想录的一段说明:代码随想录
对于一个数组,成环的话主要有如下三种情况:
- 情况一:考虑不包含首尾元素

- 情况二:考虑包含首元素,不包含尾元素
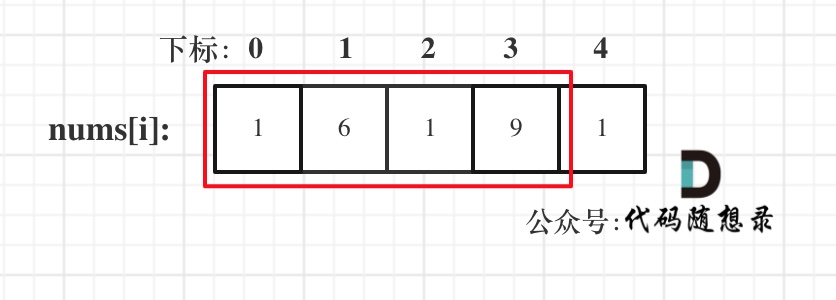
- 情况三:考虑包含尾元素,不包含首元素
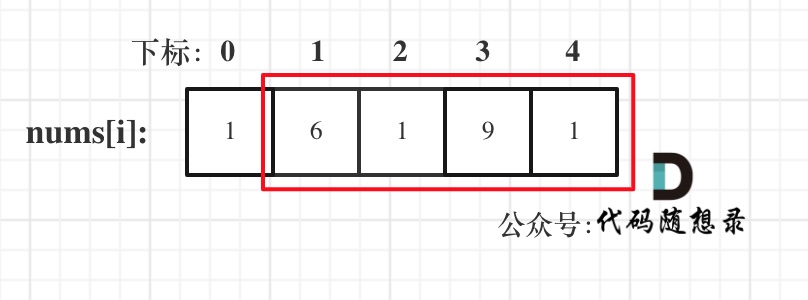
注意我这里用的是"考虑",例如情况三,虽然是考虑包含尾元素,但不一定要选尾部元素! 对于情况三,取nums[1] 和 nums[3]就是最大的。
而情况二 和 情况三 都包含了情况一了,所以只考虑情况二和情况三就可以了。
2.代码实现
1.二维数组
class Solution:
def robOne(self, nums, start, end):
n = len(nums)
dp = [[0, 0] for _ in range(n + 2)]
for i in range(start + 2, end + 3):
dp[i][0] = max(dp[i - 1])
dp[i][1] = dp[i - 1][0] + nums[i - 2]
return max(dp[end + 2])
def rob(self, nums: List[int]) -> int:
n = len(nums)
if n == 1: return nums[0]
ans1 = self.robOne(nums, 0, n - 2)
ans2 = self.robOne(nums, 1, n - 1)
return max(ans1, ans2)2.一维数组
class Solution:
def robOne(self, nums, start, end):
n = len(nums)
dp = [0] * (n + 2)
for i in range(start, end + 1):
dp[i + 2] = max(dp[(i - 1) + 2], dp[(i - 2) + 2] + nums[i])
return dp[end + 2]
def rob(self, nums: List[int]) -> int:
n = len(nums)
if n == 1: return nums[0]
ans1 = self.robOne(nums, 0, n - 2)
ans2 = self.robOne(nums, 1, n - 1)
return max(ans1, ans2)3.O1空间版
class Solution:
def rob(self, nums: List[int]) -> int:
n = len(nums)
if n == 1: return nums[0]
prev1, prev2 = 0, 0
cur1 = 0
for i in range(1, n):
# 计算当前
cur1 = max(prev1, prev2 + nums[i])
# 时间流逝
prev1, prev2 = cur1, prev1
prev1, prev2 = 0, 0
cur2 = 0
for i in range(n - 1):
# 计算当前
cur2 = max(prev1, prev2 + nums[i])
# 时间流逝
prev1, prev2 = cur2, prev1
return max(cur1, cur2)三、打家劫舍 + 二叉树
1.模式识别
当前状态 = max(打劫相邻房间, 不打劫相邻房间 + 当前房间金额)
由于二叉树不是线性结构,因此不能直接套用母题模板,需要考虑遍历顺序:
本题前序、中序和层序都不可以,只有后序可以,具体原因后面详述
2.代码实现
1.二维数组
迭代:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def rob(self, root: Optional[TreeNode]) -> int:
dp0, dp1 = collections.defaultdict(int), collections.defaultdict(int)
stk = [root]
while stk:
node = stk.pop()
if node:
stk.append(node)
stk.append(None)
if node.right: stk.append(node.right)
if node.left: stk.append(node.left)
else:
node = stk.pop()
dp1[node] = dp0[node.left] + dp0[node.right] + node.val
dp0[node] = max(dp0[node.left], dp1[node.left]) + max(dp0[node.right], dp1[node.right])
return max(dp0[root], dp1[root])递归:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def rob(self, root: Optional[TreeNode]) -> int:
def helper(node):
if not node: return 0, 0
l0, l1 = helper(node.left)
r0, r1 = helper(node.right)
dp0 = max(l0, l1) + max(r0, r1)
dp1 = l0 + r0 + node.val
return dp0, dp1
return max(helper(root))2.一维数组
迭代:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def rob(self, root: Optional[TreeNode]) -> int:
dp = collections.defaultdict(int)
stk, node, prev = [], root, None
while stk or node:
while node:
stk.append(node)
node = node.left
node = stk.pop()
if not node.right or node.right == prev:
dp0 = dp[node.left] + dp[node.right]
dp1 = node.val
if node.left: dp1 += dp[node.left.left] + dp[node.left.right]
if node.right: dp1 += dp[node.right.left] + dp[node.right.right]
dp[node] = max(dp0, dp1)
prev = node
node = None
else:
stk.append(node)
node = node.right
return dp[root]递归:(记忆化搜索)
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
memory = {}
def rob(self, root: Optional[TreeNode]) -> int:
if not root: return 0
if not root.left and not root.right: return root.val
if root in self.memory: return self.memory[root]
dp0 = self.rob(root.left) + self.rob(root.right)
dp1 = root.val
if root.left: dp1 += self.rob(root.left.left) + self.rob(root.left.right)
if root.right: dp1 += self.rob(root.right.left) + self.rob(root.right.right)
self.memory[root] = max(dp0, dp1)
return self.memory[root]3.O1空间版
二叉树不是线性结构,后序遍历有时候向上动,有时候向右动,但我估计能强行写出来,但太难写了,意义也不大
3.为什么只有后序可以?
注意打家劫舍的条件:当前状态 = max(打劫相邻房间, 不打劫相邻房间 + 当前房间金额)
即当前节点状态 = 打家劫舍函数(所有先前的相邻节点状态),
我们假设前序可以,从根节点开始,到根节点收集结果,将所有叶节点的结果算最大值
则可以写出这样的代码:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def rob(self, root: Optional[TreeNode]) -> int:
dummy1, dummy2 = TreeNode(0, root), TreeNode(0, root)
parent, dp = {root: dummy1, dummy1: dummy2}, collections.defaultdict(int)
ends = []
stk = [root]
while stk:
node = stk.pop()
dp0 = dp[parent[node]]
dp1 = dp[parent[parent[node]]] + node.val
dp[node] = max(dp0, dp1)
print(node.val, dp0, dp1)
if not node.left and not node.right: ends.append(node)
if node.right:
stk.append(node.right)
parent[node.right] = node
if node.left:
stk.append(node.left)
parent[node.left] = node
return max(dp[end] for end in ends)这样对吗?
以题干案例为例:

很显然是不对的,口算一下前序遍历的结果是6,而后序的结果也就是案例答案7,区别在哪里呢?
其实区别也很明显,前序遍历会忽略掉右下角的1
原因分析起来也很容易,也就是考虑相邻节点则前序遍历只能考虑到从上到下一条线上的结果,无法实现全局遍历
那如果将max(根节点结果)改为sum(根节点结果)行不行呢?
也不行,算一下就会知道,由于叶节点之间不相邻,所以这么做祖先节点会被重复计算
所以只有后序遍历才可以,因为
只有后序遍历才能同时实现遍历所有节点和考虑相邻状态
