当前位置：首页 > news >正文

每日一题：LeetCode-589.N叉树的前序遍历

news 2025/7/3 16:43:07

每日一题系列（day 01）

前言：

🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈

🔎🔎如果说代码有灵魂，那么它的灵魂一定是👉👉算法👈👈，因此，想要写出💚优美的程序💚，核心算法是必不可少的，少年，你渴望力量吗😆😆，想掌握程序的灵魂吗❓❗️那么就必须踏上这样一条漫长的道路🏇🏇，我们要做的，就是斩妖除魔💥💥，打怪升级！💪💪当然切记不可😈走火入魔😈，每日打怪，日日累积，终能成圣🙏🙏！今天就开启我们的斩妖之旅！✈️✈️

LeetCode-589.N叉树的前序遍历：

题目：

给定一个 n 叉树的根节点 root ，返回其节点值的前序遍历。n 叉树在输入中按层序遍历进行序列化表示，每组子节点由空值 null 分隔（请参见示例）。

示例1：

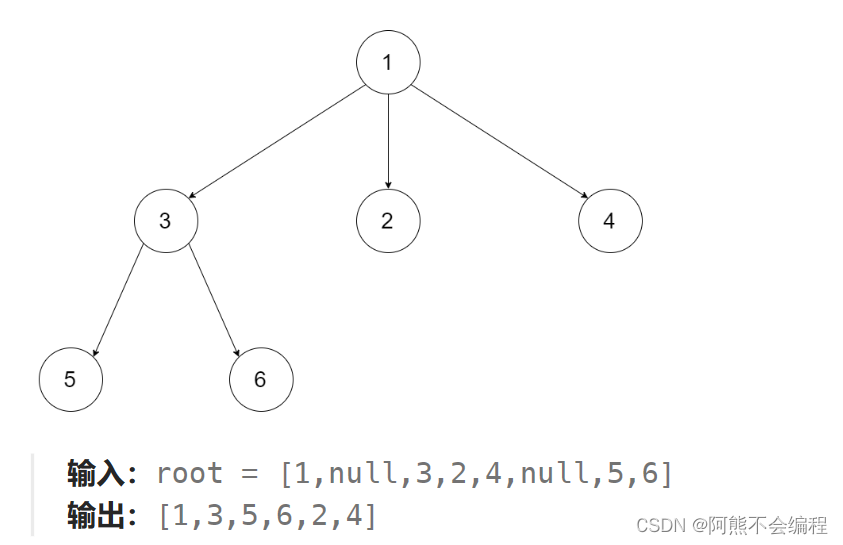
在这里插入图片描述

示例2：

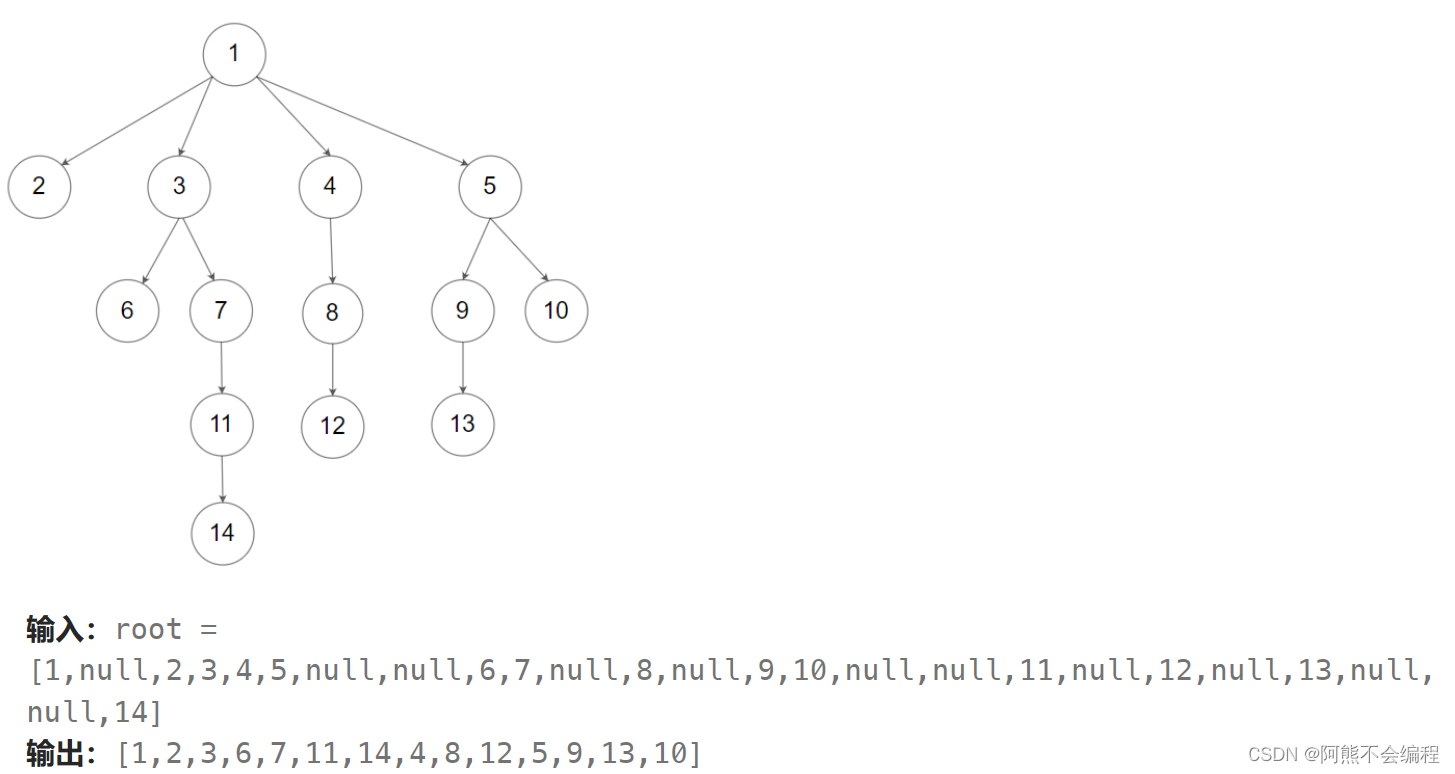
在这里插入图片描述

注意事项：

节点总数在范围 [0, 104]内
0 <= Node.val <= 104
n 叉树的高度小于或等于 1000

解法一：

思路：

首先开辟一个数组，用来存放N叉树前序遍历的结果，先将根节点压入数组，然后进行范围for（顺序遍历二叉树的每一个节点），将前序遍历的结果放入到tmp数组中，再使用范围for将tmp数组的值拷贝回原数组。最后返回原数组的值即可。

但是这样写的效率非常低，将ans数组拷贝到tmp数组，再将tmp数组拷贝回原数组，这样来来回回的拷贝效率实在是很低，所以我们可以考虑用封装来优化。

代码实现：

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val) {
        val = _val;
    }

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
public:

    vector<int> preorder(Node* root) {
        if(root == NULL) return vector<int>{};
        vector<int> ans;//开辟一个数组用来记录前序遍历结果
        ans.push_back(root -> val);//将前序遍历到的每个节点的值压入到数组中
        for(auto x : root -> children)//范围for依次遍历N叉树的每个节点
        {
            vector<int> tmp = preorder(x);//用tmp数组接收前序遍历的结果
            for(auto y : tmp) ans.push_back(y);//拷贝完成之后再将tmp数组元素拷贝回原数组
        }
        return ans;//返回前序遍历数组的结果即可
    }
};

解法二：

思路：

以上是不使用封装解决前序遍历问题的方法，没有什么问题是一层封装解决不了的，如果有，那就两层。

1、我们在preorder函数中定义一个数组ans用来记录前序遍历结果，封装一个前序遍历的函数，将根节点和数组传ans入函数，其中数组传参是用引用传参（避免多一次拷贝）最后返回数组即可。
2、在函数内部，我们首先将遍历到的每个节点的值压入到数组ans当中，再使用范围for对N叉树的每个子孩子遍历，并且将前序遍历到的节点全部拷贝到ans数组中。

时间复杂度：O(N)，其中 n 为 N 叉树的节点。每个节点恰好被遍历一次。
空间复杂度：O(N)，递归过程中需要调用栈的开销，平均情况下为 O(log⁡N)，最坏情况下树的深度为 N−1，此时需要的空间复杂度为 O(N)。

代码实现：

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val) {
        val = _val;
    }

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
public:
  void _preorder(Node *root, vector<int> &ans)//引用传参，少一次拷贝构造
    {
        if(root == NULL) 
        return;
        ans.push_back(root -> val);//将前序遍历的节点值压入数组中
        for(auto x : root -> children)//范围for便利
        {
            _preorder(x, ans);//将前序遍历结果也压入到ans数组中
        }
        return;
    }

    vector<int> preorder(Node* root) {
        vector<int> ans;//记录前序遍历的结果
        _preorder(root, ans);//进行前序遍历
        return ans;//返回前序遍历的数组
    }
};