数据结构代码复习 持续更新

1.BST的计数

思路：

得到数组后从小到大排序，每插入一个数后，那个数就变成了一个隔板，假如插入的数是数组的未插入元素的边界那么隔板就在边界，无效果

假如插入的数是数组中间，隔板就在中间，此时下一步选择隔板左的数或隔板右的数，最后形成的树是等价的 比如123 选择2，那么后面选择13还是31树形相同。
整个问题就可以从小大到DP解决：

直接计算隔板左的数有多少种不同组合，隔板右的数有多少种不同组合。

最小问题：

1个数的BST 1个

2个数的BST 2个

3个数的BST 5个

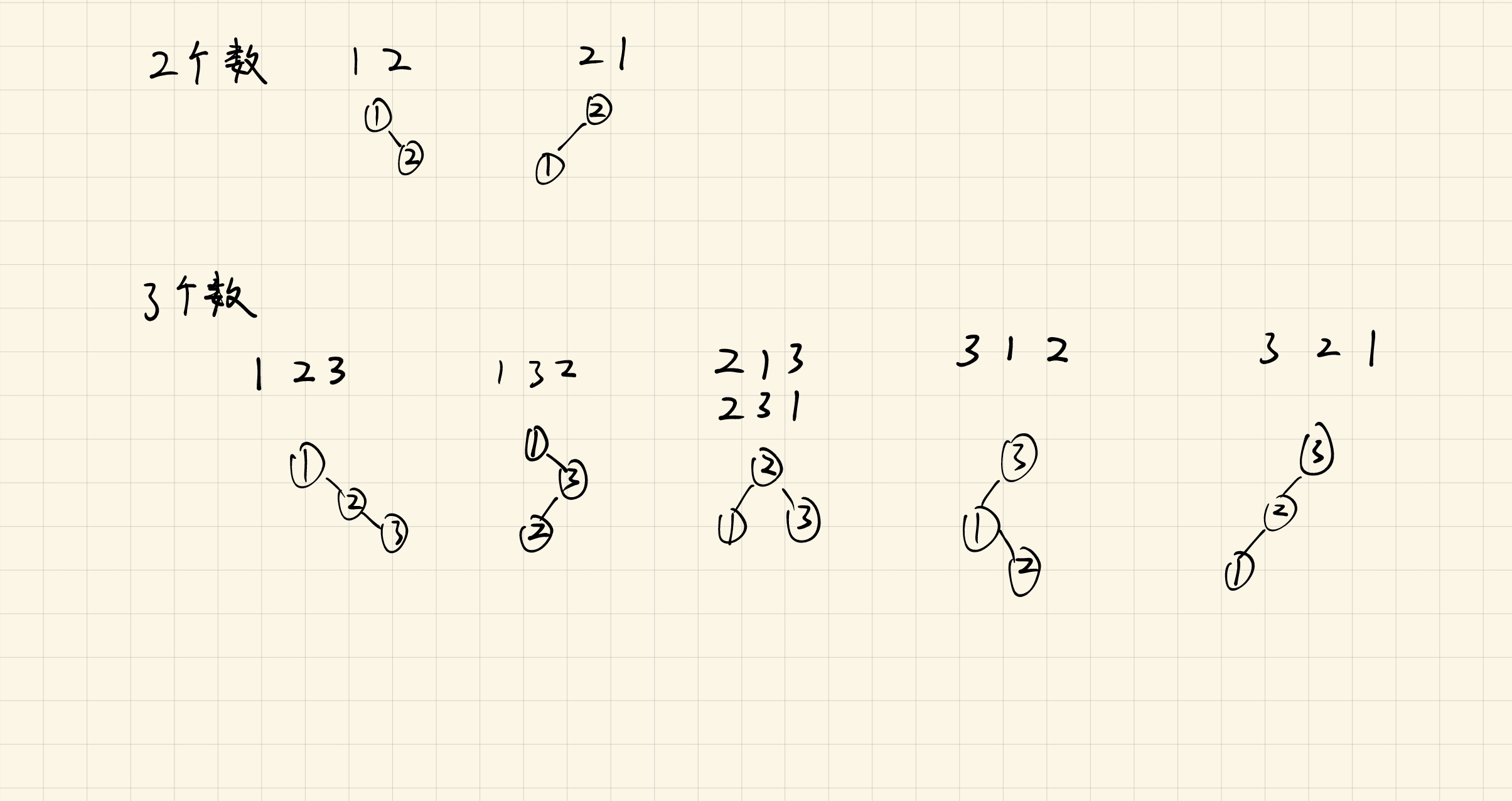
4个数可以利用之前的得到的结果解题：

如果你在疑问为什么隔板两边要相乘，来看5个的插入

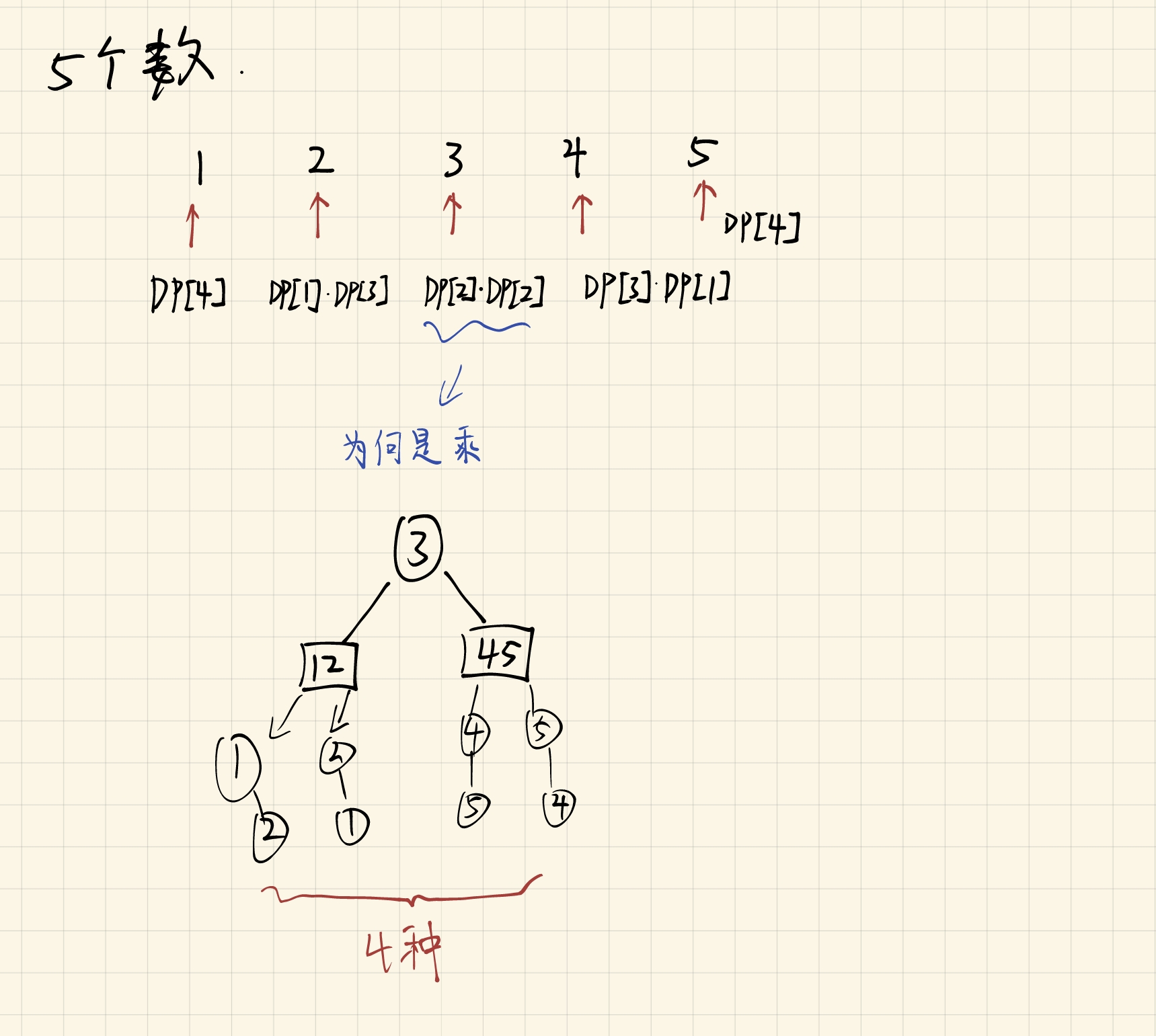
那么就得到关键代码：

for(int i =1;i<n;i++)
{for(int j=0;j<i;j++){dp[i]=dp[i]+(dp[j]*dp[i-j-1]);}} 

来看整体代码：

#include <iostream>
#include <vector>
using namespace std;const int MOD = 1000000007;int main() {int T;cin >> T;vector<int> testCases(T);int maxN = 0;// 读取所有测试用例并找到最大的n值for (int i = 0; i < T; i++) {cin >> testCases[i];if (testCases[i] > maxN) {maxN = testCases[i];}}// 动态规划计算Catalan数vector<long long> dp(maxN + 1, 0);dp[0] = 1; // 基础情况：0个节点只有1种空树for (int i = 1; i <= maxN; i++) {for (int j = 0; j < i; j++) {// 状态转移方程：dp[i] = Σ (dp[j] * dp[i - j - 1])dp[i] = (dp[i] + (dp[j] * dp[i - j - 1]) % MOD) % MOD;}}// 输出结果for (int i = 0; i < T; i++) {cout << dp[testCases[i]] << endl;}return 0;
}

这相当于一种求和：

如果你写下了这些代码并想到了展开，恭喜你得到卡特兰数