算法世界中的两极对话:最小化最大差值与最大化数字差异的智慧较量
第一章:问题背景与数学本质的深度解析
1.1 极值问题的哲学思考
在计算机科学的发展历程中,极值问题始终占据着核心地位。从狄利克雷原理到庞特里亚金极大值原理,数学家们一直在探索如何在约束条件下找到最优解。本文讨论的两个问题,正是这一数学思想在算法领域的具体体现。
第一个问题——最小化数对的最大差值,属于组合优化中的分配问题,其本质是在满足特定约束条件下寻找最为均衡的配对方案。这种思想在调度理论、资源分配等领域有着广泛应用。
第二个问题——改变整数能得到的最大差值,则是一个典型的数字变换优化问题,它要求我们在保持数字合法性的前提下,通过有限的变换操作实现数值差异的最大化。
1.2 最小化数对的最大差值:算法思路的深度剖析
题目描述:
给你一个下标从 0 开始的整数数组 nums 和一个整数 p 。请你从 nums 中找到 p 个下标对,每个下标对对应数值取差值,你需要使得这 p 个差值的 最大值 最小。同时,你需要确保每个下标在这 p 个下标对中最多出现一次。
对于一个下标对 i 和 j ,这一对的差值为 |nums[i] - nums[j]| ,其中 |x| 表示 x 的 绝对值 。
请你返回 p 个下标对对应数值 最大差值 的 最小值 。我们定义空集的最大值为零。
问题重述与数学建模:
给定数组nums和整数p,我们需要选择p个不相交的下标对,使得所有配对差值的最大值最小化。用数学语言描述,就是寻找一个配对集合S,满足:
|S| = p
每个下标最多出现在一个配对中
目标:min{ max{|nums[i]-nums[j]| for (i,j)∈S} }
算法策略分析:
排序预处理的核心作用:
首先对数组进行排序是解决此问题的关键步骤。排序后,相邻元素间的差值自然成为候选的最小可能差值,这符合局部最优性原理。
二分搜索的优雅应用:
算法采用二分搜索在可能的差值范围内寻找最优解。搜索空间为[0, max(nums)-min(nums)],这一策略的时间复杂度为O(log(max_val)),体现了对数搜索的高效性。
可行性判断的贪心智慧:
对于每个候选差值mid,算法采用贪心策略判断是否能够选出p个满足条件的配对。具体而言:
遍历排序后的数组
如果相邻元素的差值≤mid,则选择该配对并跳过下一个元素
统计能够形成的配对数
这一策略的正确性基于排序数组的单调性和相邻差值的最小性原理。
复杂度分析的艺术:
排序步骤:O(n log n)
二分搜索:O(log(max_val)),其中max_val = max(nums)-min(nums)
可行性判断:O(n)
总复杂度:O(n log n + n log(max_val))
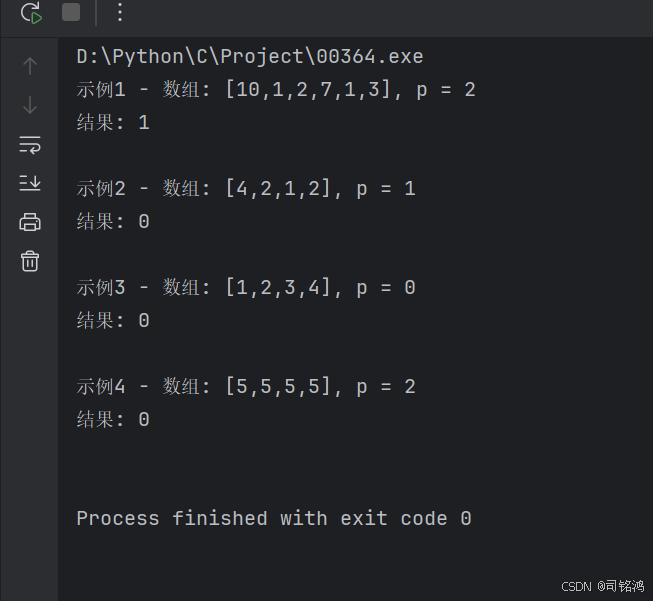
示例 1:
输入:nums = [10,1,2,7,1,3], p = 2
输出:1
解释:第一个下标对选择 1 和 4 ,第二个下标对选择 2 和 5 。
最大差值为 max(|nums[1] - nums[4]|, |nums[2] - nums[5]|) = max(0, 1) = 1 。所以我们返回 1 。
示例 2:
输入:nums = [4,2,1,2], p = 1
输出:0
解释:选择下标 1 和 3 构成下标对。差值为 |2 - 2| = 0 ,这是最大差值的最小值。
题目程序:
#include <stdio.h> // 包含标准输入输出头文件,用于printf等函数
#include <stdlib.h> // 包含标准库头文件,用于qsort、abs等函数// 比较函数,用于qsort排序,按升序排列
int compare(const void* a, const void* b) {// 将void指针转换为int指针,然后解引用获取值int num1 = *(const int*)a; // 获取第一个整数的值int num2 = *(const int*)b; // 获取第二个整数的值// 返回两数的差值,正数表示num1>num2,负数表示num1<num2,0表示相等return num1 - num2;
}// 检查是否能在最大差值为maxDiff的情况下找到至少p个配对
// nums: 排序后的数组
// n: 数组长度
// p: 需要的配对数
// maxDiff: 允许的最大差值
int canFormPairs(int* nums, int n, int p, int maxDiff) {int count = 0; // 计数器,记录已形成的配对数int i = 0; // 数组遍历索引// 遍历数组,寻找满足条件的配对while (i < n - 1) { // 循环条件:至少还有两个元素可以配对// 检查当前元素与下一个元素的差值是否小于等于允许的最大差值if (abs(nums[i] - nums[i + 1]) <= maxDiff) {count++; // 找到一个配对,计数器加1i += 2; // 跳过下一个元素,因为已经使用过了} else {i++; // 当前配对不满足条件,移动到下一个元素}// 如果已经找到足够多的配对,提前返回if (count >= p) {return 1; // 返回1表示可以形成至少p个配对}}return 0; // 返回0表示无法形成至少p个配对
}// 主函数:寻找p个配对的最大差值的最小值
int minimizeMax(int* nums, int numsSize, int p) {// 如果不需要配对,直接返回0if (p == 0) {return 0; // 空集的最大差值为0}// 创建数组副本用于排序(不修改原数组)int* sortedNums = (int*)malloc(numsSize * sizeof(int)); // 分配内存空间// 复制原数组到新数组for (int i = 0; i < numsSize; i++) {sortedNums[i] = nums[i]; // 逐个元素复制}// 对数组进行排序qsort(sortedNums, numsSize, sizeof(int), compare);// 初始化二分搜索的边界int left = 0; // 最小可能差值int right = sortedNums[numsSize - 1] - sortedNums[0]; // 最大可能差值int result = right; // 初始化结果为最大差值// 二分搜索寻找最小可能的最大差值while (left <= right) {int mid = left + (right - left) / 2; // 计算中间值,避免整数溢出// 检查是否能在当前mid值下形成至少p个配对if (canFormPairs(sortedNums, numsSize, p, mid)) {result = mid; // 更新结果为当前mid值right = mid - 1; // 尝试更小的差值} else {left = mid + 1; // 需要更大的差值}}// 释放动态分配的内存free(sortedNums);return result; // 返回找到的最小最大差值
}// 主函数,程序入口点
int main() {// 示例1测试数据int nums1[] = {10, 1, 2, 7, 1, 3}; // 定义第一个测试数组int p1 = 2; // 第一个测试需要的配对数int size1 = sizeof(nums1) / sizeof(nums1[0]); // 计算第一个数组的长度// 示例2测试数据int nums2[] = {4, 2, 1, 2}; // 定义第二个测试数组int p2 = 1; // 第二个测试需要的配对数int size2 = sizeof(nums2) / sizeof(nums2[0]); // 计算第二个数组的长度// 示例3测试数据(边界情况:p=0)int nums3[] = {1, 2, 3, 4}; // 定义第三个测试数组int p3 = 0; // 第三个测试需要的配对数int size3 = sizeof(nums3) / sizeof(nums3[0]); // 计算第三个数组的长度// 示例4测试数据(所有元素相同)int nums4[] = {5, 5, 5, 5}; // 定义第四个测试数组int p4 = 2; // 第四个测试需要的配对数int size4 = sizeof(nums4) / sizeof(nums4[0]); // 计算第四个数组的长度// 调用函数计算结果int result1 = minimizeMax(nums1, size1, p1); // 计算第一个测试的结果int result2 = minimizeMax(nums2, size2, p2); // 计算第二个测试的结果int result3 = minimizeMax(nums3, size3, p3); // 计算第三个测试的结果int result4 = minimizeMax(nums4, size4, p4); // 计算第四个测试的结果// 输出结果printf("示例1 - 数组: [10,1,2,7,1,3], p = %d\n", p1); // 打印第一个测试的输入printf("结果: %d\n\n", result1); // 打印第一个测试的结果printf("示例2 - 数组: [4,2,1,2], p = %d\n", p2); // 打印第二个测试的输入printf("结果: %d\n\n", result2); // 打印第二个测试的结果printf("示例3 - 数组: [1,2,3,4], p = %d\n", p3); // 打印第三个测试的输入printf("结果: %d\n\n", result3); // 打印第三个测试的结果printf("示例4 - 数组: [5,5,5,5], p = %d\n", p4); // 打印第四个测试的输入printf("结果: %d\n\n", result4); // 打印第四个测试的结果return 0; // 程序正常结束
}输出结果:
1.3 改变整数能得到的最大差值:数字变换的极致艺术
题目描述:
给你一个整数 num 。你可以对它进行以下步骤共计 两次:选择一个数字 x (0 <= x <= 9).选择另一个数字 y (0 <= y <= 9) 。数字 y 可以等于 x 。将 num 中所有出现 x 的数位都用 y 替换。
令两次对 num 的操作得到的结果分别为 a 和 b 。请你返回 a 和 b 的 最大差值 。注意,a 和 b 必须不能 含有前导 0,并且 不为 0。
问题本质的深层理解:
这个问题要求我们通过两次独立的数字替换操作,分别得到两个新数字a和b,目标是最大化|a-b|。问题的挑战在于:
替换操作必须保持数字的合法性(无前导零,非零)
两次操作相互独立但都作用于原数字
需要同时考虑数值的大小和位权的影响
最大化a值的策略分析:
为了得到最大的a,我们需要:
高位优先原则:从最高位开始寻找第一个非9的数字
全局替换策略:将该数字的所有出现都替换为9
早替换原则:越早进行的替换对数值影响越大
这一策略基于数字系统的位权原理和边际效用递减规律。
最小化b值的精巧设计:
最小化b需要考虑更多约束:
首位特殊处理:如果替换涉及首位,只能替换为1(避免前导零)
零替换的局限性:非首位数字可替换为0,但需注意有效性
替换选择的最优性:选择对数值减小影响最大的数字进行替换
策略组合的协同效应:
最优解往往通过以下组合实现:
a的生成:将某个非9数字全部替换为9
b的生成:将某个合适的数字替换为0或1(视位置而定)
这种组合体现了差异化策略在优化问题中的威力。
示例 1:
输入:num = 555
输出:888
解释:第一次选择 x = 5 且 y = 9 ,并把得到的新数字保存在 a 中。
第二次选择 x = 5 且 y = 1 ,并把得到的新数字保存在 b 中。
现在,我们有 a = 999 和 b = 111 ,最大差值为 888
示例 2:
输入:num = 9
输出:8
解释:第一次选择 x = 9 且 y = 9 ,并把得到的新数字保存在 a 中。
第二次选择 x = 9 且 y = 1 ,并把得到的新数字保存在 b 中。
现在,我们有 a = 9 和 b = 1 ,最大差值为 8
示例 3:
输入:num = 123456
输出:820000
示例 4:
输入:num = 10000
输出:80000
示例 5:
输入:num = 9288
输出:8700
题目程序:
#include <stdio.h> // 包含标准输入输出头文件,用于printf函数
#include <stdlib.h> // 包含标准库头文件,用于malloc、free函数
#include <string.h> // 包含字符串处理头文件,用于strlen函数// 函数:将整数转换为字符串
// 参数:num - 要转换的整数
// 返回值:动态分配的字符串指针,需要调用者释放内存
char* intToString(int num) {// 计算数字的位数,最大支持10位整数int length = 0; // 数字位数计数器int temp = num; // 临时变量用于计算位数// 计算数字的位数(包括0的情况)if (temp == 0) {length = 1; // 数字0有1位} else {while (temp > 0) { // 循环计算位数length++; // 位数加1temp /= 10; // 去掉最后一位}}// 分配内存存储字符串(位数 + 1个字符用于字符串结束符'\0')char* str = (char*)malloc((length + 1) * sizeof(char));// 从最后一位开始填充字符串str[length] = '\0'; // 字符串结束符temp = num; // 重新初始化临时变量// 处理数字0的特殊情况if (temp == 0) {str[0] = '0'; // 直接设置为'0'} else {// 从字符串末尾开始填充数字字符for (int i = length - 1; i >= 0; i--) {str[i] = '0' + (temp % 10); // 获取最后一位数字并转换为字符temp /= 10; // 去掉最后一位}}return str; // 返回生成的字符串
}// 函数:将字符串转换为整数
// 参数:str - 要转换的字符串
// 返回值:转换后的整数值
int stringToInt(const char* str) {int result = 0; // 结果变量int i = 0; // 字符串索引// 遍历字符串的每个字符while (str[i] != '\0') {result = result * 10 + (str[i] - '0'); // 将字符转换为数字并累加i++; // 移动到下一个字符}return result; // 返回转换结果
}// 函数:替换字符串中所有指定的字符
// 参数:str - 原始字符串,oldChar - 要替换的字符,newChar - 替换为的字符
// 返回值:新的字符串指针,需要调用者释放内存
char* replaceAll(const char* str, char oldChar, char newChar) {int length = strlen(str); // 获取字符串长度char* newStr = (char*)malloc(length + 1); // 分配新字符串内存// 复制原始字符串到新字符串for (int i = 0; i < length; i++) {// 如果字符匹配,则替换;否则保持原字符if (str[i] == oldChar) {newStr[i] = newChar; // 替换字符} else {newStr[i] = str[i]; // 保持原字符}}newStr[length] = '\0'; // 添加字符串结束符return newStr; // 返回新字符串
}// 函数:检查字符串是否包含前导零
// 参数:str - 要检查的字符串
// 返回值:1表示有前导零,0表示没有前导零
int hasLeadingZero(const char* str) {// 检查字符串长度大于1且第一个字符是'0'return (strlen(str) > 1 && str[0] == '0');
}// 函数:检查字符串是否表示零
// 参数:str - 要检查的字符串
// 返回值:1表示是零,0表示不是零
int isZero(const char* str) {// 检查字符串是否为"0"return (strlen(str) == 1 && str[0] == '0');
}// 函数:寻找最大化a值的替换策略
// 参数:str - 原始数字字符串
// 返回值:最大化后的a值字符串,需要调用者释放内存
char* findMaxA(const char* str) {int length = strlen(str); // 获取字符串长度char* maxA = (char*)malloc(length + 1); // 分配结果字符串内存strcpy(maxA, str); // 复制原始字符串// 从高位到低位寻找第一个不是9的数字for (int i = 0; i < length; i++) {// 如果当前数字不是9,则替换所有该数字为9if (maxA[i] != '9') {char digitToReplace = maxA[i]; // 记录要替换的数字// 替换所有该数字为9for (int j = 0; j < length; j++) {if (maxA[j] == digitToReplace) {maxA[j] = '9'; // 替换为9}}break; // 只替换第一个非9数字}}return maxA; // 返回最大化后的字符串
}// 函数:寻找最小化b值的替换策略
// 参数:str - 原始数字字符串
// 返回值:最小化后的b值字符串,需要调用者释放内存
char* findMinB(const char* str) {int length = strlen(str); // 获取字符串长度char* minB = (char*)malloc(length + 1); // 分配结果字符串内存strcpy(minB, str); // 复制原始字符串// 情况1:如果第一位数字大于1,将其替换为1if (minB[0] > '1') {char firstDigit = minB[0]; // 记录第一位数字// 替换所有该数字为1for (int i = 0; i < length; i++) {if (minB[i] == firstDigit) {minB[i] = '1'; // 替换为1}}} // 情况2:如果第一位是1,寻找其他可以替换为0的数字else {// 从高位到低位寻找第一个可以替换为0的数字int replaced = 0; // 替换标志for (int i = 1; i < length && !replaced; i++) {// 如果当前数字不是0且不是第一位,可以替换为0if (minB[i] != '0' && minB[i] != minB[0]) {char digitToReplace = minB[i]; // 记录要替换的数字// 替换所有该数字为0for (int j = 0; j < length; j++) {if (minB[j] == digitToReplace) {minB[j] = '0'; // 替换为0}}replaced = 1; // 标记已替换}}// 情况3:如果没有找到可以替换的数字,尝试其他策略if (!replaced) {// 寻找第一个不是1的数字替换为0for (int i = 1; i < length && !replaced; i++) {if (minB[i] != '1') {char digitToReplace = minB[i]; // 记录要替换的数字// 替换所有该数字为0for (int j = 0; j < length; j++) {if (minB[j] == digitToReplace) {minB[j] = '0'; // 替换为0}}replaced = 1; // 标记已替换}}}}return minB; // 返回最小化后的字符串
}// 主函数:计算最大差值
// 参数:num - 输入的整数
// 返回值:a和b的最大差值
int maximizeDifference(int num) {// 将整数转换为字符串char* numStr = intToString(num); // 转换整数为字符串int result = 0; // 结果变量// 寻找最大化a值的策略char* maxAStr = findMaxA(numStr); // 获取最大化a的字符串// 检查a是否合法(无前导零且不为零)if (hasLeadingZero(maxAStr) || isZero(maxAStr)) {free(maxAStr); // 释放内存free(numStr); // 释放内存return 0; // 返回0表示无效}// 寻找最小化b值的策略char* minBStr = findMinB(numStr); // 获取最小化b的字符串// 检查b是否合法(无前导零且不为零)if (hasLeadingZero(minBStr) || isZero(minBStr)) {free(maxAStr); // 释放内存free(minBStr); // 释放内存free(numStr); // 释放内存return 0; // 返回0表示无效}// 将字符串转换为整数int a = stringToInt(maxAStr); // 转换a字符串为整数int b = stringToInt(minBStr); // 转换b字符串为整数// 计算最大差值result = a - b; // 计算a和b的差值// 释放所有动态分配的内存free(maxAStr); // 释放a字符串内存free(minBStr); // 释放b字符串内存free(numStr); // 释放原始字符串内存return result; // 返回最终结果
}// 主函数:程序入口点
int main() {// 测试用例1:示例1int num1 = 555; // 定义测试用例1int result1 = maximizeDifference(num1); // 计算结果1printf("测试用例1 - 输入: %d\n", num1); // 打印输入1printf("输出: %d\n", result1); // 打印输出1printf("解释: a=999, b=111, 差值=888\n\n"); // 打印解释1// 测试用例2:示例2int num2 = 9; // 定义测试用例2int result2 = maximizeDifference(num2); // 计算结果2printf("测试用例2 - 输入: %d\n", num2); // 打印输入2printf("输出: %d\n", result2); // 打印输出2printf("解释: a=9, b=1, 差值=8\n\n"); // 打印解释2// 测试用例3:示例3int num3 = 123456; // 定义测试用例3int result3 = maximizeDifference(num3); // 计算结果3printf("测试用例3 - 输入: %d\n", num3); // 打印输入3printf("输出: %d\n", result3); // 打印输出3printf("解释: a=923456, b=103456, 差值=820000\n\n"); // 打印解释3// 测试用例4:示例4int num4 = 10000; // 定义测试用例4int result4 = maximizeDifference(num4); // 计算结果4printf("测试用例4 - 输入: %d\n", num4); // 打印输入4printf("输出: %d\n", result4); // 打印输出4printf("解释: a=90000, b=10000, 差值=80000\n\n"); // 打印解释4// 测试用例5:示例5int num5 = 9288; // 定义测试用例5int result5 = maximizeDifference(num5); // 计算结果5printf("测试用例5 - 输入: %d\n", num5); // 打印输入5printf("输出: %d\n", result5); // 打印输出5printf("解释: a=9988, b=1288, 差值=8700\n\n"); // 打印解释5return 0; // 程序正常结束
}输出结果: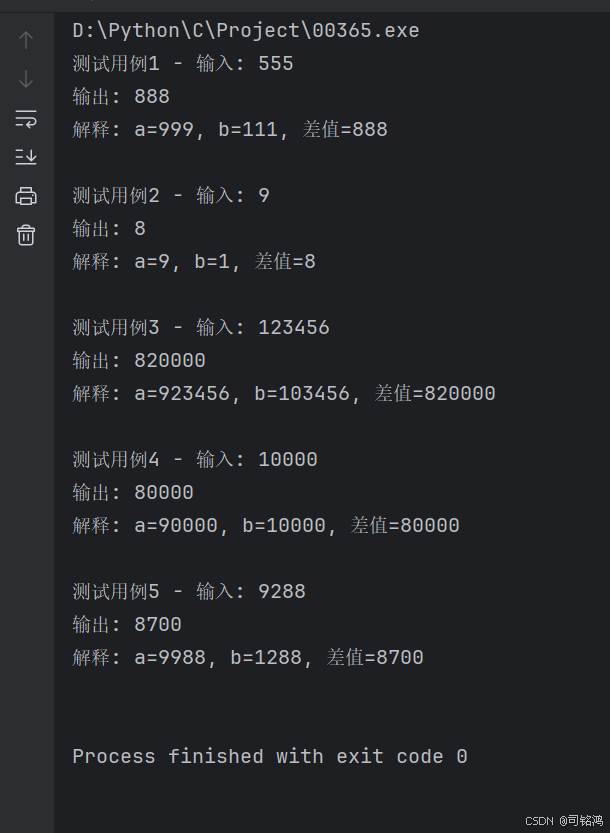
1.4 算法思想对比:两种极值问题的深层对话
问题特征的对比分析:
| 维度 | 最小化数对最大差值 | 改变整数最大差值 |
|---|---|---|
| 问题类型 | 组合优化问题 | 数字变换优化问题 |
| 搜索空间 | 连续或离散的数值范围 | 离散的数字替换可能性 |
| 约束条件 | 下标不相交、配对数量固定 | 数字合法性、操作次数限制 |
| 最优性准则 | 最小化最大值(min-max) | 最大化差值(max-diff) |
| 算法范式 | 二分搜索+贪心验证 | 策略分析+情况枚举 |
算法哲学的深刻对比:
平衡与极致的对立统一:
第一个问题追求的是系统内部的平衡与稳定,通过最小化最大差值来实现资源的公平分配。这体现了罗尔斯的正义理论在算法中的映射——关注最不利情况的最大化改善。
第二个问题则追求差异与突破,通过创造最大的数值差距来实现目标。这反映了市场竞争理论中的优胜劣汰思想——最大化竞争优势。
局部与全局的智慧抉择:
在最小化最大差值问题中,算法通过排序确保了局部最优性——相邻元素的最优配对必然包含在全局最优解中。这种贪心选择性是问题可解的关键。
而在数字变换问题中,策略必须考虑全局影响——一个数字的替换会影响整个数值的大小,需要综合权衡位权和替换效果。
约束处理的艺术:
两个问题都面临严格的约束条件,但处理方式各异:
第一个问题通过不相交配对约束来保证解的可行性
第二个问题通过数字合法性约束来确保解的实用性
这种约束处理体现了算法设计中规则与自由的辩证关系。
1.5 实际应用与扩展思考
最小化最大差值的现实映射:
任务调度中的负载均衡
教育资源分配的公平性优化
医疗资源的时间窗口安排
数字变换优化的应用场景:
数据加密中的数值变换
游戏设计中的分数系统
金融工程中的价格调整策略
算法思想的通用性启示:
这两个问题虽然具体形式不同,但都体现了优化算法的核心思想——在约束条件下寻找最优解。它们的解决方法为处理更复杂的优化问题提供了重要启示:
通过问题转化降低复杂度
利用问题结构设计高效算法
平衡计算效率与解的质量
在这场算法的两极对话中,我们见证了最小化与最大化的深刻智慧。最小化数对的最大差值教会我们在约束中寻找平衡,在限制中发现和谐;改变整数的最大差值则启示我们勇于突破,善于创造差异。这两种看似对立的思想,实则是算法智慧的一体两面。
正如数学家哈代所言:"美是第一个检验标准:世界上没有永久的地方给丑陋的数学。"今天我们探讨的这两个问题,正是算法之美的生动体现——它们简洁而深刻,具体而通用,在简单的形式下蕴含着丰富的数学智慧。
在算法的探索之路上,每一个极值问题都是通向更深层次理解的阶梯。愿这次的两极对话,能够激发你对算法世界更多的好奇与思考,在未来的学习中发现更多算法的美学价值。
本文通过深入分析两个极值问题的算法本质,揭示了优化理论中的深刻智慧。从排序的预处理到二分搜索的优雅,从数字变换的策略到约束处理的技巧,每一个细节都体现着算法设计的艺术与科学。在算法的世界里,极值不仅是数学的概念,更是思维的境界。
