卫星通信天线的极化角定义、计算、与位置和姿态的关系

卫星通信天线的极化角定义、计算、与位置和姿态的关系

天线控制器根据载体的姿态信息（通过安装在载体上的惯导获得），卫星的位置（通过卫星星历计算得到），载体的位置（通过GPS定位得到），能够计算出天线的波束指向（方位角和俯仰角）。天线的伺服机构通过电机控制天线转动相应的角度，使得天线波束中心在几何上正好对准卫星。

天线波束中心对准卫星之后，还不能保证天线能够正常接收卫星信号，这里还有一个极化角匹配的问题。

什么是天线的极化角

极化角 (Polarization Angle): 指的是卫星下行信号的电场矢量方向，与地面天线本地水平面之间的夹角。

为什么会存在天线极化角？

天线极化角是由卫星和地面天线本身的几何关系造成的。

• • 同步卫星通常在赤道上空。卫星发射的信号有水平极化信号，也会有垂直极化信号。卫星天线发射的信号的极化（例如“垂直极化”）是相对于地球赤道平面来定义的。下面是常见卫星发射的信标信号的频率和极化，其中V代表垂直，H代表水平。

卫星信标信号

• • 由于地球是一个球体。地面天线在地球表面的任何一个位置，都有一个自己的“本地水平面”。
• •卫星信号的“垂直极化”方向，投影到地面天线所在位置的“本地水平”参考系上时，不可能是完全的垂直的，而是会产生一个倾斜角，这就是极化角的由来。因此，除了正好处在卫星正下方（星下点）经线上的地区，对于其他绝大多数地区的地面天线而言，天线接收的卫星信号都存在不同的极化角。
• • 极化角就是：为了让地面天线能“正对”卫星信号的极化方向，需要旋转一个角度。否则就会产生极化失配，信号接收效率大幅下降

---

我们可以举一个形象的例子说明天线俯仰角方位角和极化角的关系：

我们把卫星下行信号像一把锁的“锁孔”，天线馈源就像一个“钥匙”。

• • 方位角和俯仰角对准卫星，相当于将“钥匙”精确地对准“锁孔”，但是钥匙插入锁孔之后，锁还不能打开。
• • 旋转极化角相当于钥匙插进锁孔之后，再旋转一个角度，当钥匙的齿牙跟锁芯对齐的时候，锁就打开了。相反，如果齿牙和锁芯不匹配，锁就打不开。

相应的，如果天线的极化角和卫星信号的电场矢量方向不匹配，天线会产生极化失配，无法最大效率的接收信号能量。而当极化角偏差是90°时，天线几乎接收不到信号，导致通信中断。

---

举例说明：

假设天线在北京，要对准一颗位于赤道上空、经度偏西的同步卫星，该卫星发射的信号是垂直极化，这个垂直极化是相对于赤道平面垂直的。

• • 地面天线要想完成对星，首先需要将天线的方位角朝向西南方向，并抬起一定的俯仰角，完成了几何方向的对准卫星。
• • 如果卫星信号到达地面天线时，相对于地面天线的本地水平面，是向右下方倾斜了20°，所以必须将天线的馈源（LNB）向反方向（逆时针）旋转20°来进行补偿。

极化角是怎么计算的？

我们来讨论这个问题：

天线安装在汽车上，跟踪的是地球同步卫星。刚开始汽车静止，天线伺服机构已经调整方位角、俯仰角和极化角完成对星。然后汽车以100km/h的速度前进，在前进的过程中，通过调整方位角和俯仰角保证天线一直对准卫星，但是不调整天线极化角，随着汽车位置的变化，天线极化角的变化有多少度？

定性计算过程如下：

我们把卫星、汽车的出发点、汽车1小时之后的终点，建立一个三角形：

• • 顶点A： 地球同步轨道上的卫星。
• • 顶点B： 汽车的出发点。
• • 顶点C： 汽车一小时后的终点。

在这个三角形中，边AB和边AC的长度都是约等于36,000公里，而边BC的长度仅为100公里，从顶点A（卫星）看下来，B点和C点之间的夹角（视角变化）非常非常小。

由于极化角是由“天线-卫星”相对几何位置决定的，汽车位置移动100km导致的“天线-卫星”的相对几何关系的改变微乎其微，所以极化角变化也是非常微小的。

定量计算：

极化角计算公式

根据《卫星通信》（Satellite Communications）by Timothy Pratt, Charles W. Bostian, Jeremy E. Allnutt中提到的，天线极化角的计算公式如下：

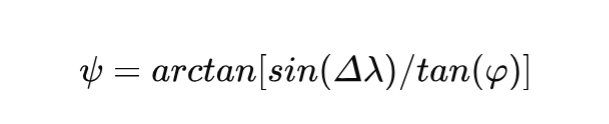
其中φ是地面天线所在地的纬度（北纬为正，南纬为负），Δλ是卫星星下点的经度与地面天线所在地的经度之差。

当卫星的经度和地面天线的经度相同时，Δλ=0，则ψ = arctan [ sin(0) / tan(φ) ] = arctan(0) = 0°。此时地面天线的极化角等于0°。

案例说明：天线移动100km，极化角变化多大？

场景设定：

• • 卫星位置： 东经101°的地球同步卫星。
• • 汽车初始位置 (A点): 北纬40°，东经85°。
• • 汽车运动： 沿东经85°经线，向正北方向行驶100公里。

计算过程：

• • 计算经度差 (Δλ)：

经度差是地面天线经度与卫星经度的差值，在本次行程中，汽车的经度不变，因此 Δλ 是一个常数。 Δλ = λ_ant - λ_sat = (85°) - (101°) = -16°

• • 计算纬度变化

地球的纬度每度对应的南北距离约为111.32公里。

纬度变化量 Δφ ≈ 100 km / 111.32 km/° ≈ 0.898°

为了便于计算，我们可近似为 0.9°，因此汽车终点（B点）位置的纬度是

φ_B = φ_A + Δφ = 40° + 0.9° = 40.9°

• • 计算A点的极化角

`ψ_A = arctan[sin(-16°) / tan(40°)]` 
`ψ_A = arctan[0.2756 / 0.8391]` 
`ψ_A ≈ -18.18°

• • 计算B点的极化角
  `ψ_B = arctan[sin(-16°) / tan(40.9°)]`
  `ψ_B = arctan[0.2756 / 0.8662]`
  `ψ_B ≈ -17.66°
• • 极化角变化

Δψ = ψ_B - ψ_A = -17.66° - （-18.18°） = 0.52°

载体位置变化100km，极化角变化了0.52°。

同理我们可以计算出，载体位置变化1000km，极化角变化4.8°。

极化角还跟载体姿态相关

我们来讨论这个问题：

载体姿态变化的情况下，由于天线伺服系统首先会根据载体姿态变化调整了天线指向，保证天线波束中心始终指向卫星，这种情况下，姿态引起的极化角变化有多少度？

天线俯仰/方位伺服系统在补偿姿态变化以保持天线对星指向的同时，无法自动修正姿态变化而产生的极化角误差，极化角偏差不会被消除。

假设载体的姿态变化是：

• • Δr: 横滚角（Roll）变化量
• • Δp: 俯仰角（Pitch）变化量
• • Δy: 偏航角（Yaw）变化量

根据载体姿态，卫星位置，天线位置计算得到的天线指向角：

• • Az: 方位角（Azimuth）
• • El: 俯仰角（Elevation）

姿态变化影响极化角 (ΔPol)的公式 可以通过下面这个经典的运动学近似公式来计算

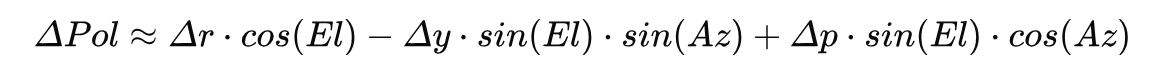
为了简化和聚焦于主要影响，在许多动中通天线控制的应用中，当方位角 Az 不在0°或180°附近时，sin(Az) ≈ 1，cos(Az) ≈ 0，上面的公式可以进一步简化为：

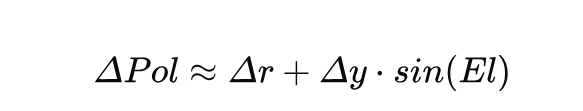
由上面的公式可以得知：

1. 1. 载体横滚角变化是影响极化角最直接，最重要的分量，载体横滚角的变化几乎是一对一的直接转换为极化角的变化。
2. 2. 载体偏航角度的影响跟天线的俯仰角相关

• • 当 El = 0 (天线水平指向地平线):sin(El) = 0，此时偏航对极化角没有影响。
• • 当 El = 90 (天线垂直指向天顶):sin(El) = 1，此时 ΔPol ≈ Δr + Δy。

1. 3. 载体的俯仰角变化对极化角的影响相对较小。

下面是几个典型场景下，载体姿态变化对极化角的影响。

场景	载体姿态变化	天线俯仰角(El)	主要影响项	所需极化角修正 ΔPol (约)
场景1： 船舶在风浪中	横滚 Δr = +10° (偏航 Δy ≈ 0)	30°	横滚主导	10° + 0 * sin(30°) = 10°
场景2： 飞机进入转弯	偏航 Δy = +20° (横滚已由天线补偿)	45°	偏航主导	0 + 20° * sin(45°) = 14.1°
场景3： 汽车在立交桥上盘旋	偏航 Δy = +90° (90度转弯)	60° (卫星位置较高)	偏航效应显著	0 + 90° * sin(60°) = 77.9°

⚠️ 这些变化如果不做实时补偿，将会导致严重的极化失配，甚至通信中断！

总结

要点	内容
✅ 极化角是信号接收的必备匹配条件之一	只靠方位角+俯仰角对准卫星还不够
✅ 极化角随地面位置变化而变化	经纬度差 16°，极化角可变十几度
✅ 极化角也受载体姿态影响	特别是横滚和偏航角度
✅ 姿态变化引起的极化角偏差不能靠伺服系统自动补偿	必须由控制算法修正

在下一章，我们将介绍极化角偏差对天线增益的影响、对交叉极化隔离度的影响。