基础算法---【双指针】

前言：

        双指针算法有时候也叫尺取法或者滑动窗⼝，是⼀种优化暴⼒枚举策略的⼿段：当我们发现在两层 for 循环的暴⼒枚举过程中，两个指针是可以不回退的，此时我们就可以利⽤两个指针不回退的性质来优化时间复杂度。 因为双指针算法中，两个指针是朝着同⼀个⽅向移动的，因此也叫做同向双指针。⼀定要学会如何从暴⼒解法优化成双指针算法。

题目一：唯一的雪花

        https://www.luogu.com.cn/problem/UVA11572

解题思路

        根据题目的意思，其实就是在一组数据里边找到不重复的最大一段连续的数据。

        首先思考一下暴力解法，可以用两层循环来解决一下这个题目，第一层for循环里边的i表示起点，第二层for循环就负责去寻找以i为起点，j为终点的一段没有重复数据的区间，如果j便利到了重复的数字，那么就代表区间 [i，j] 里边已经存在重复元素了，此时i++，也就是改变区间起点，继续去寻找以i为起点，j为终点的最大不重复区间。

        如何处理数据的不重复？可以使用哈希表来实现。

        以上就是暴力解法，其时间复杂度毫无疑问是0(n ^ 2)的，严重超时了。但是我们可以顺着暴力解法的思想去寻找优化的方案，请看下图。

        双层for循环的时间复杂度之所以高就是因为它把所有的情况全部枚举了出来，每当出现了一个重复的元素，left和right都要重新指向下一个起始位置，对于圈3(上图所示)来说，绿色框出的部分是没有重复元素的，但就是由于里边有个3，当right指向3的时候就和前边的3重复了，在下标为[1,3]这个区间里边，right其实是没有必要回退的，因为每次right走的都是重复的区间，而且每次right走到3的时候都会导致区间内的元素发生重复。当left指向4的时候，right也没有必要回退到4的位置，因为4，5两个元素是会要便利到的。因此，经过上边的分析，我们得出这道题目的两个指针是不用回退的，就可以用双指针来解决这道题。

        使用双指针来解决问题需要考虑几件事情

   1.初始化指针以及如何维护窗口里边的数据

   2.进窗口

   3.判断窗口是否合法

   4.出窗口

   5.更新结果

        对于本题来说：以上5点分别如下。

        1.left和right都初始化成1(数组从下标为1的地方开始存)，利用unordered_map来维护数据，里边存两个数据，分别为元素以及元素出现的次数，即为unordered_map<int , int>。

        2.凡是right指向的数据都要进入窗口

        3.如果哈希表里边记录的数据出现两次，窗口就不合法了，需要出窗口。

        4.出窗口就是left指向的数据要出去

        (其中3，4两点需要循环执行)

        5.最后要统计出最大的那个区间。

代码实现

#include<iostream>
#include<unordered_map>
using namespace std;const int N = 1e6 + 10;
int n, T;
int a[N];//存放最一开始的数据
unordered_map<int, int> mp;int main()
{int ret = 0;//存放最终结果cin >> T;while (T--){cin >> n;for (int i = 1; i <= n; i++){cin >> a[i];}//初始化int left = 1, right = 1;while (right <= n){//进窗口mp[a[right]]++;while (mp[a[right]] > 1){//非法窗口处理mp[a[left]]--;left++;}ret = max(ret, right - left + 1);right++;}cout << ret << endl;}return 0;
}

题目二：逛画展

        https://www.luogu.com.cn/problem/P1638

解题思路

        题目的意思就是在一组数据之中找到最小的区间，在这个区间里边必须要包括1~m的所有数字。

        首先还是考虑暴力解法，跟上题一样，两层for循环枚举出所有可能的区间，然后去挑出里边最短的一个符合条件的区间。如何知道每一个数字出现的次数以及怎么判断所有在1~m的数字都在区间里边呢？还是使用哈希表来存储某一个数字出现的次数，再另外定义一个变量kind去表示1~m里边的数字是否都在区间内部。如果哈希表里边这个数字出现的次数是由0变成1的，那么说明区间里边多增加了一个我们想要的数字，此时kind++。

   2 5 3 1 3 2 4 1 1 5 4 3

   以上是题给出的数据，还是需要left和right两个指针，其中红色部分是我们找到的第一个区间，此时kind == m，如果right再往后走就会导致区间非法。此时需要left++往前走，但right就没有必要回退了，因为left到right之间的数据还是会进入到哈希表。

        经过以上的分析，我们就发现双指针不回退的性质，因此就可以使用同向双指针来优化本题。只需要搞明白以下5件事就可以了。

   1.初始化指针以及如何维护窗口里边的数据

   2.进窗口

   3.判断窗口是否合法

   4.出窗口

   5.更新结果

        1.初始化left = 1，right = 1，left ~ right之间的数据存在哈希表里边，kind变量和哈希表是捆绑在一起的，通过判断哈希表里边数字出现的次数是否为0来改变kind值，kind是记录1~m里边有几个数字在left~right区间里边了。

        2.right指向的数据进窗口

        3~5.如果kind < m，说明区间还是合法的，如果kind == m，区间不合法，就需要让left指向的数据出窗口，在出窗口前要更新一下结果，此时这个窗口的区间长度是多少。

代码实现

#include<iostream>
using namespace std;const int N = 1e6 + 10,M = 2e3 + 10;
int a[N];int mp[M];
int kind;int main()
{int n, m;cin >> n >> m;for (int i = 1; i <= n; i++) cin >> a[i];//初始化int left = 1, right = 1;int x = 1;//x即为题意里边的xint ret = n;//最终的区间长度，初始化成最差情况就行while (right <= n){//进窗口//由0->1，kind++if (mp[a[right]]++ == 0){kind++;}//判断是否合法while (kind == m){//更新结果int len = right - left + 1;//如果len == ret就不用更新，因为之前的x肯定<现在的leftif (len < ret){ret = len;x = left;}//由1->0，kind--if (mp[a[left]]-- == 1){kind--;}left++;}right++;}cout << x << " " << x + ret - 1 << endl;return 0;
}

题目三：丢手绢

        https://ac.nowcoder.com/acm/problem/207040

解题思路

         要想找到两个距离最远的小朋友，得先知道每一个小朋友离其最远的小朋友，最后取一个最大的距离就可以了。而题目对于距离的定义是有两个方向，顺时针和逆时针，这就导致可能有两个离他最远的小朋友，也可能只有一个(当顺时针和逆时针的距离一样的时候)。

        如何去寻找距离最远的小朋友呢？请看下图。

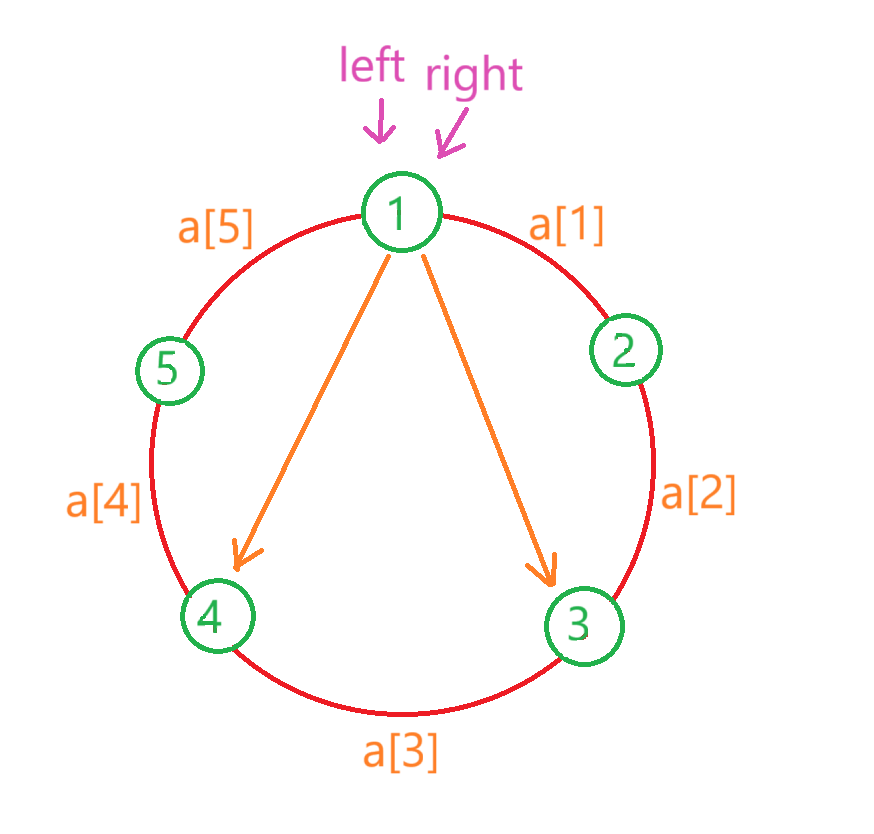
        上图的a[i]表示第1个小朋友到第i+1个小朋友的距离，假设所有a[i]加起来的总距离为sum，1~3顺时针距离为k(此时的 k < (sum / 2) )，如果k再累加一个a[3]，此时k > (sum / 2)，那么3号小朋友就是1号小朋友顺时针方向的最远小朋友。同理，4号小朋友就是1号小朋友逆时针方向的最远小朋友。接下来比比1~3(顺时针)的距离长还是1~4(逆时针)的距离长就行了。至此，我们就找到了离1号小朋友最远的那个小朋友。

        根据上边的方法，我们可以暴力枚举出所有小朋友的最远小朋友，最后取一个最大值就是最终的结果。遇到循环嵌套，就要看一看能不能用同向双指针去优化，left和right一开始是指向的1，当right向前走的时候，right指向的位置就入窗口了，同时累加最远距离k，直到k > (sum / 2)，即为非法区间，一旦遇到非法区间，left++，此时right确实没有必要回退，因为随着left++，k其实是在变小，就不可能 > (sum / 2)，肯定是合法区间，right++就可以了。

        最后一个要解决的问题就是什么时候更新结果，当区间非法的时候，right指向的位置其实就是逆时针距离i号小朋友最远的距离，此时的结果其实就是sum - k，而当区间合法的时候，k就是我们要的结果。

        以上就包括了双指针解法必须要提前分析好的5件事情，分析清楚就可以写代码了。

   1.初始化指针以及如何维护窗口里边的数据

   2.进窗口

   3.判断窗口是否合法

   4.出窗口

   5.更新结果

代码实现

#include<iostream>
using namespace std;const int N = 1e5 + 10;
//存相邻两个小朋友之间的距离
//a[i]表示i~i+1号小朋友之间的距离
long long a[N];
long long sum;//一整个环形的总长度
long long ret;//存放最后的结果
int n;int main()
{cin >> n;for (int i = 1; i <= n; i++){cin >> a[i];sum += a[i];}//初始化int left = 1, right = 1;long long k = 0;//left~right之间的距离while (right <= n){//入窗口k += a[right];//判断是否合法while (2 * k >= sum){//更新结果---逆时针的最长距离ret = max(ret, sum - k);//出窗口k -= a[left];left++;}ret = max(ret, k);//顺时针的最长距离right++;}cout << ret << endl;return 0;
}