当前位置：首页 > news >正文

Stable Diffusion原理解析

news 2025/10/1 17:36:28

1. Stable Diffusion原理

论文：High-Resolution Image Synthesis with Latent Diffusion Models

预备知识

分布

$qσ(xt–1∣xt,x0)=N(xt–1;αt–1x0+1−αt–1−σt2ϵθ(xt,t)⏟中心位置,σt2I⏟波动大小)q_{\sigma}(x_{t\text{--}1}|x_{t},x_{0})=\mathcal{N}\Big(x_{t\text{--}1}; \underbrace{\sqrt{\alpha_{t\text{--}1}}x_{0}+\sqrt{1-\alpha_{t\text{--}1}- \sigma_{t}^{2}} \epsilon_{\theta}(x_{t},t)}_{\text{中心位置}},\underbrace{ \sigma_{t}^{2}I}_{\text{波动大小}}\Big)$

$qσ(xt−1∣xt,x0)q_{\sigma}(x_{t-1} \mid x_t, x_0)$
- 读作：在已知 $x_t$ 和 $x_0$ 的情况下， $x_{t-1}$ 的概率分布。
- 换句话说，它不是一个具体的数，而是“描述 $x_{t-1}$ 可能长什么样子的一套规则”。
- 这里的下标 $σ\sigma$ 表示：这个分布取决于一个参数 $σt\sigma_t$ ，它控制分布里“随机性”的大小。
$N(xt–1;αt–1x0+1−αt–1−σt2ϵθ(xt,t)⏟中心位置,σt2I⏟波动大小)\mathcal{N}\Big(x_{t\text{--}1}; \underbrace{\sqrt{\alpha_{t\text{--}1}}x_{0}+\sqrt{1-\alpha_{t\text{--}1}- \sigma_{t}^{2}} \epsilon_{\theta}(x_{t},t)}_{\text{中心位置}},\underbrace{ \sigma_{t}^{2}I}_{\text{波动大小}}\Big)$
- $N\mathcal{N}$ 表示 高斯分布（正态分布）
- $N(x;μ,Σ)\mathcal{N}(x;\mu, \Sigma)$ 表示“变量 x 服从均值为 $μ\mu$ ，方差/协方差为 $Σ\Sigma$ 的高斯分布”。
- 在公式里：
  $N(xt−1;αt−1x0+1−αt−1−σt2ϵθ(xt,t)⏟均值μ,σt2I⏟方差Σ)\mathcal{N}\Big(x_{t-1};\underbrace{\sqrt{\alpha_{t-1}}x_{0}+\sqrt{1-\alpha _{t-1}-\sigma_{t}^{2}} \epsilon_{\theta}(x_{t},t)}_{\text{均值} \mu}, \underbrace{\sigma_{t}^{2}I}_{\text{方差} \Sigma}\Big)$
  均值（中心位置） = $αt−1x0+1−αt−1−σt2ϵθ(xt,t)\sqrt{\alpha_{t-1}} x_0 + \sqrt{1-\alpha_{t-1}-\sigma_t^2}\epsilon_\theta(x_t,t)$ ，表示“主要往这个方向靠”。
  
  方差（波动大小） = $σt2I\sigma_t^2 I$ ，表示“在均值附近有多少随机抖动”。

DDPM

DDPM 是最早的扩散模型之一，它通过一个 逐步加噪与去噪的马尔科夫过程 来学习数据分布。

正向扩散 (Forward Process)
从真实图像 $x_0$ 出发，在 (T) 步中逐渐加入高斯噪声，直到变成各向同性高斯分布：
$q(xt∣xt−1)=N(xt;1−βtxt−1,βtI)q(x_t|x_{t-1}) = \mathcal{N}(x_t; \sqrt{1-\beta_t}x_{t-1}, \beta_t I)$
最终 $xT∼N(0,I)x_T \sim \mathcal{N}(0, I)$ 。
反向生成 (Reverse Process)
学习一个神经网络（通常是 U-Net）去近似反向条件概率：
$pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),Σθ(xt,t)){p_{\theta}(x_{t-1}|x_{t})=\mathcal{N}(x_{t-1};\mu_{\theta}(x_{t},t),\Sigma _{\theta}(x_{t},t))}$

利用采样公式 $x=μ+σz,z∼N(0,I)x=\mu+\sigma z, z \sim \mathcal{N}(0, I)$ 后：
$xt−1=1at(xt−1−at1−atϵ0(xt,t))+σtzx_{t-1}= \frac{1}{ \sqrt{a_{t}}} \left( x_{t}- \frac{1-a_{t}}{ \sqrt{1-a_{t}}} \epsilon_{0} \left( x_{t},t \right) \right)+ \sigma_{t}z$
采样过程
需要逐步从 $\to 0$ 采样，通常是几百到上千步，采样效率比较低。

DDIM

DDPM 的缺点：
- 必须逐步采样，生成速度慢。
- 每一步是随机采样（有方差），不易控制生成轨迹。
DDIM 的改进目标：
- 提供 确定性采样（无需随机噪声）。
- 可以 跳步采样（减少采样步数）。
- 保持生成质量的同时提升速度。
核心原理

1. 非马尔科夫过程

DDIM 并不强制要求反向过程是马尔科夫链，而是构造一个新的反向过程，直接定义：
$qσ(xt–1∣xt,x0)=N(xt–1;αt–1x0+1−αt–1−σt2ϵθ(xt,t),σt2I)q_{\sigma}(x_{t\text{--}1}|x_{t},x_{0})=\mathcal{N}\Big(x_{t\text{--}1}; \sqrt{\alpha_{t\text{--}1}}x_{0}+\sqrt{1-\alpha_{t\text{--}1}-\sigma_{t}^{2}} \epsilon_{\theta}(x_{t},t),\sigma_{t}^{2}I\Big)$

其中 $ϵθ(xt,t)\epsilon_\theta(x_t, t)$ 是预测噪声。
参数 $σt\sigma_t$ 控制采样是否确定性：
- 若 $σt=0\sigma_t = 0$  → 采样是确定性的（DDIM）。
- 若 $σt=βt\sigma_t = \sqrt{\beta_t}$ → 退化为 DDPM。

2. 确定性采样

当 $σt=0\sigma_t = 0$ 时，DDIM 的采样方程变为：
$xt−1=μσ=αt−1x0+1−αt−1−σt2ϵθ(xt,t).xt−1=αt−1x0+1−αt−1ϵθ(xt,t){x}_{t-1}={\mu}_{\sigma}=\sqrt{{\alpha}_{t-1}}{x}_{0}+\sqrt{{1 }-{\alpha}_{t-1}-{\sigma}_{t}^{2}} {\epsilon}_{\theta}({x}_{t}, {t}). \\ x_{t-1} = \sqrt{\alpha_{t-1}} x_0 + \sqrt{1-\alpha_{t-1}} \epsilon_\theta(x_t, t)$

这样采样过程没有随机性，生成结果可复现。 $x_0$ 是从当前 $x_t$ 和预测噪声估计出的清晰图像。

$xt−1=μσ{x}_{t-1}={\mu}_{\sigma}$ 是因为 $σt=0\sigma_t = 0$ ，方差为 0，抖动完全消失。数学上，这个分布变成点质量（delta），所有概率质量都集中在 $μ\mu$ 上。因此从这个分布里采样的唯一可能值就是它的均值： $xt−1=μσ{x}_{t-1}={\mu}_{\sigma}$ 。

3. 跳步采样

根据 $xt−1=αt−1x0+1−αt−1ϵθ(xt,t)x_{t-1} = \sqrt{\alpha_{t-1}} x_0 + \sqrt{1-\alpha_{t-1}} \epsilon_\theta(x_t, t)$ 反推 $x_0$ :
$x0=xt−1−αˉt⋅ϵθ(xt,t)αˉt{x_{0}}=\frac{{x_{t}}-\sqrt{1-\bar{{\alpha}}_{t}}\cdot{\epsilon_{ \theta}(x_{t},t)}}{\sqrt{\bar{{\alpha}}_{t}}}$

例如，我们每20个时刻取一个，我们可以直接用上述公式推导每次都可以得到当前时刻的 $x_0$ 。由于 DDIM 的采样公式是显式的，可以直接在更稀疏的时间步上采样（例如从 1000 步跳到 50 步），大幅提升生成速度。

1.1 概述

Stable Diffusion 基于潜在扩散模型（Latent Diffusion Models, LDMs），通过将图像生成过程从像素空间（原图大小）转移到潜在空间（低维度大小），显著降低了计算复杂度，同时保持了高质量的图像生成能力。

Stable Diffusion 的核心思想是结合扩散模型的强大生成能力与自动编码器的高效表示学习。传统扩散模型如 DDPM 直接在像素空间操作，计算成本极高。Stable Diffusion 通过引入潜在空间，将高维图像数据压缩到低维潜在表示，再在该空间进行扩散过程，大幅减少了计算量。

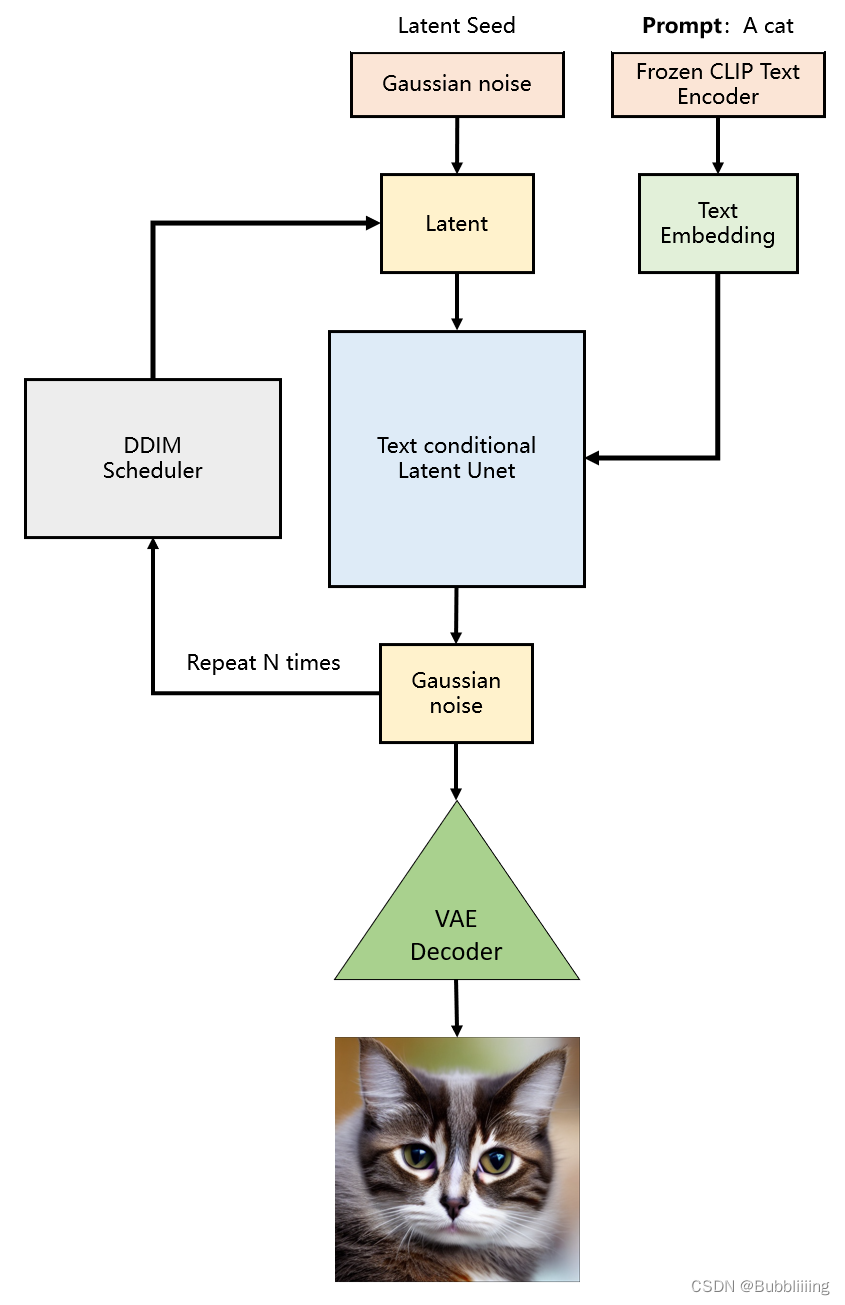
下图是Stable Diffusion生成图片的具体过程：

可以看到，对于输入的文字会经过一个CLIP对文字编码，然后和初始图像（初始化使用随机高斯噪声Gaussian Noise）一起输入去噪模块（也就是图中Text conditioned latent U-Net），最后生成一只猫。

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

1.2 Forward(扩散过程)

扩散过程与DDPM一样，区别是Stable Diffusion是在潜空间中生成噪声，它会经过VAE生成低维度向量，最后也可以使用VAE还原为指定维度的图片。VAE是变分自编码器，可以将输入图片进行编码，一个高宽原本为512x512x3的图片在使用VAE编码后会变成64x64x4，这个4是人为设定的，不必纠结为什么不是3。这个时候我们就使用一个简单的矩阵代替原有的512x512x3的图片了，传输与存储成本就很低。在实际要去看的时候，可以对64x64x4的矩阵进行解码，获得512x512x3的图片。

因此，如果我们生成的噪声是相对于隐空间的，同时我们要生成一个512x512x3的图片，那么我们就要初始化一个64x64x4的隐向量，我们在隐空间扩散好后，再使用解码器就可以生成512x512x3的图像。

Stable Diffusion会先训练一个自编码器，来学习将图像压缩成低维表示。

通过训练好的编码器 $E$ ，可以将原始大小的图像压缩成低维的latent data（图像压缩）
通过训练好的解码器 $D$ ，可以将latent data还原为原始大小的图像

在将图像压缩成latent data后，便可以在latent space中完成扩散过程，对比下和Diffusion扩散过程的区别，如下图所示：

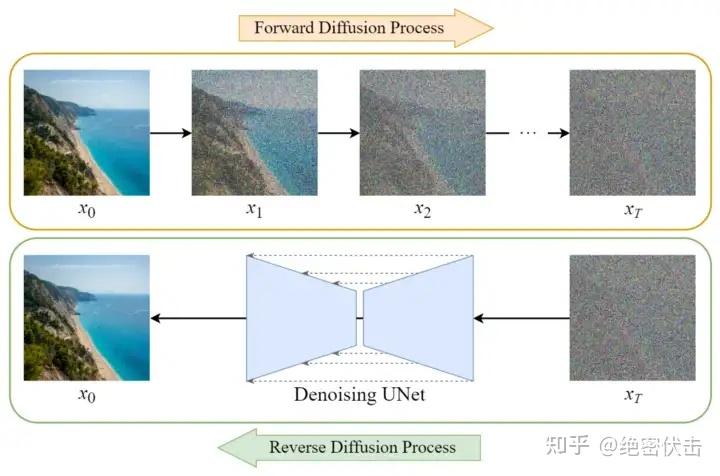
外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

可以看到Diffusion扩散模型就是在原图上进行的操作，而Stale Diffusion是在压缩后的图像 $z$ 上进行操作。

1.3 Backward(去噪过程)

去噪过程是扩散模型的生成阶段，通过学习到的模型逐步去除噪声，恢复潜在表示。Stable Diffusion 使用条件化的 UNet 架构作为去噪模型 $ϵθ\epsilon_\theta$ ，其输入为当前带噪潜在表示 $z_t$ 、时间步 t 及条件信息 y（如文本提示）。模型预测当前步骤的噪声，从而得到去噪后的潜在表示。

在这里插入图片描述

1.4 Training

与DDPM类似，训练目标是使模型能够准确预测扩散过程中添加的噪声。损失函数为均方误差，衡量模型预测的噪声与实际噪声的差异。

Stable Diffusion在反向扩散过程中其实谈不上改进，只是支持了文本的输入，对U-Net的结构做了修改，使得每一轮去噪过程中文本和图像相关联。

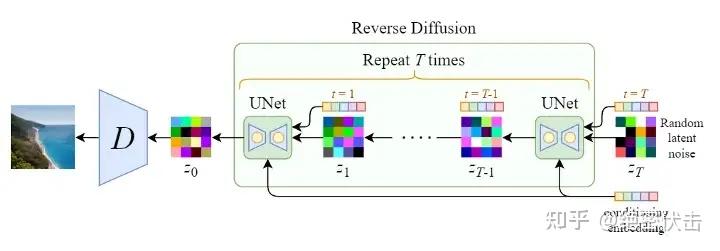
外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

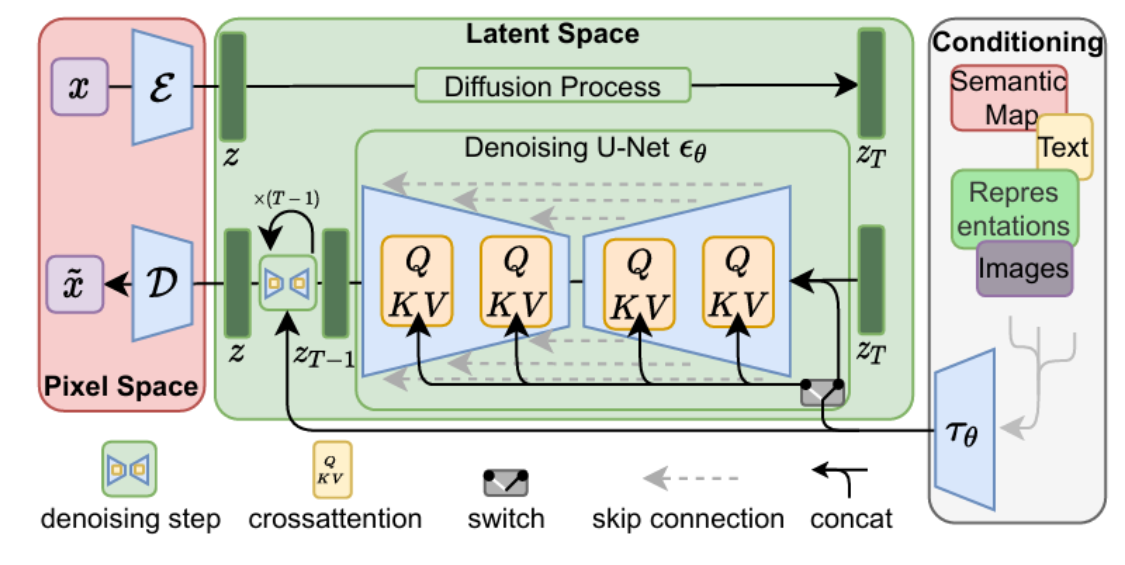
从上图可以看出，反向扩散过程中输入文本和初始图像 $Z_T$ 需要经过 $T$ 轮的U-Net网络（ $T$ 轮去噪过程），最后得到输出 $Z_0$ ，解码后便可以得到最终图像。由于要处理文本向量，因此必然要对U-Net网络进行调整，这样才能使得文本和图像相关联。下图是单轮的去噪过程：

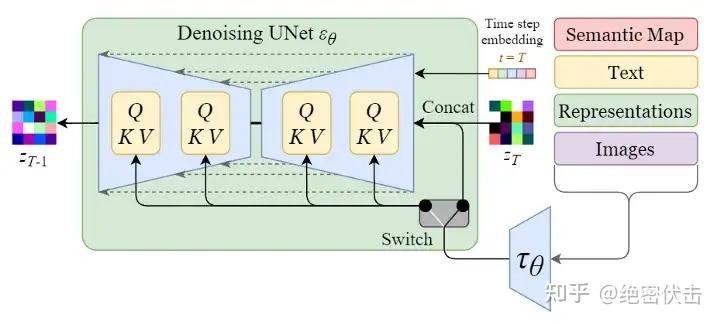
在这里插入图片描述

上图的最左边里面的Semantic Map、Text、Representations、Images稍微不好理解，这是Stable Diffusion处理不同任务的通用框架，用于控制图像生成的内容：

Semantic Map：表示处理的是通过语义生成图像的任务，输入是一张语义分割图（每个像素对应一个类别标签），模型根据这张“颜色编码的语义图”生成符合语义的图像。
- 输入一张城市街景的语义图：绿色区域 = 树木，灰色 = 道路，蓝色 = 天空。
- 模型生成一张真实风格的城市街景照片，其中每块区域的内容和语义图一致。
Text：表示的就是文字生成图像的任务，输入是自然语言描述（prompt），模型根据文字生成图像。
- 输入：“一只穿着西装的猫在月球上打高尔夫”
- 输出：一张风格化或写实图像，内容完全符合文本描述。
Representations：表示的是通过语言描述生成图像，通常是通过 BERT/CLIP 等文本编码器 提取的语义嵌入（embedding），用于引导图像生成。
- 输入文本：“夕阳下的雪山”
- 文本编码器将其转换为一个 512 维向量（representation），模型通过这个向量生成一张夕阳照射雪山的图像
- 注意：虽然和 “Text” 类似，但 “Representations” 更强调中间语义向量，而不是原始文本。
Images：表示的是根据图像生成图像，输入是一张已有的图像，模型基于这张图像进行图像到图像的转换（image-to-image translation）。
- 输入一张黑白线稿图
- 输出一张自动上色的彩色图像

这里我们只考虑输入是Text，因此首先会通过模型CLIP模型生成文本向量，然后输入到U-Net网络中的多头Attention(Q, K, V)。
$Attention(Q,K,V)=softmax(QKTd)⋅V\text{Attention}\left(Q,K,V\right)=\text{softmax}\left(\frac{QK^{T}}{\sqrt{d}} \right)\cdot V$
其中：

$Q=WQ⋅zT,K=WK⋅τθ(y),V=WV⋅τθ(y)Q=W_{Q}\cdot z_{T},K=W_{K}\cdot\tau_{\theta}\left(y\right),V=W_{V}\cdot\tau_{ \theta}\left(y\right)$ 。可以看到每一轮去噪过程中，文本向量 $τθ(y)\tau_{\theta}\left(y\right)$ 会和当前图像 $z_T$ 计算相关性。