知识表示与处理4

相关特征、无关特征、冗余

定义：从M中选择N个特征，准则函数可以达到最优解

搜索过程+选择准则

搜索过程：实践上，非穷举方法，找到次优解

循序向前选择法SFS

选最好的单个特征，从其他特征与它组合选最好的，直到达到特征数

缺点：单个特征去分离差，两个特这个结合区分力强，此时SFS失效

循序向后选择法SBS

一个一个去掉，也是贪心

选择准则：判断某个特征子集是否优于另一个，有监督或是无监督

1训练好分类器后的泛化误差

2定义类内距离度量来描述某个特征子集的可分度

类内距离：

1.类内散度

设有c个类别，Di表示第i个样本集，

m为每个类的类中心

2.均方距离

降维问题

不同的训练目标：PCA，LDA，LLR...

PCA主成分分析

多变量问题

PCA前提假设，数据符合正态分布；若分布为均匀或是圆则失效

二维中为椭圆，投影到长轴这边，分布好区分；四维中有四个轴，也是选最长的轴

若坐标系与椭圆的长短轴平行，那么长轴描述了数据的主要变化

但一般不平行

矩阵的旋转变换，矩阵相乘

缺点：无监督，无法处理实时数据

LDA线性判别分析

PCA两个类有重叠部分无法区分

LDA，类间区分

每个类计算协方差矩阵

基本瑞利商  xAX  大于最小特征值，小于最大特征值

基本瑞利商-广义瑞利商（有B）

不同点：LDA为有监督降维方法，最多只能降到（类别数-1）维

LDA 的目标是：最大化类间散度（between-class scatter）的同时最小化类内散度（within-class scatter）

在数学上，这等价于求解广义特征值问题：

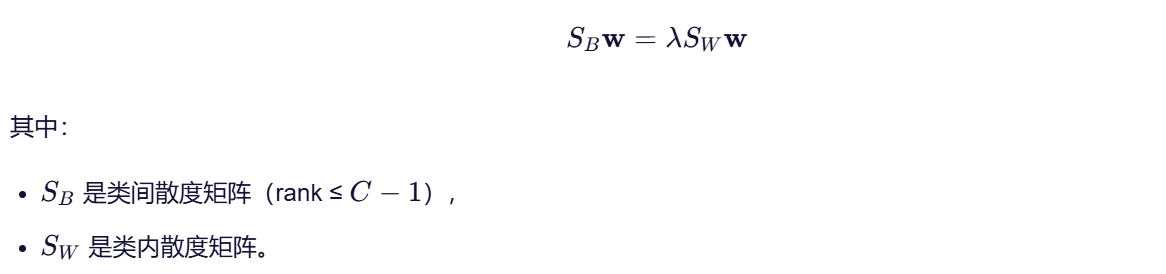
关键点在于：类间散度矩阵 SB​ 的秩最多为 C−1

LLE局部线性嵌入

假设在小的局部是线性的，可以由周围的几个点线性表示，需要学习权重系数

低维空间中的投影，依然保持如何的权重关系

学习w，每个样本都有一个权重，损失函数：

在低维，用相同的w，损失函数为 sum(yi-sum_k(wyj))

流形正则项 J(Y) = tr(YMY)

对于图，图中 L+||WMW||2 ,其中M为邻接矩阵