Heteroskedasticity

Heteroskedasticity come from

The passage is describing heteroskedasticity, a situation where the variance of the error term ( $ϵ$ ) is not constant but depends on the explanatory variable (x).
In ordinary regression we usually assume homoskedasticity: ($\text{Var}(ϵ)={\sigma }^2$), the same for all values of $(x)$. But here, the idea is that when (x) is large in magnitude, the spread (variance) of the errors is also larger. In probabilistic terms, if ($\text{Var}(ϵ)$) grows with (x), then the probability that ($ϵ$) takes on large positive or negative values increases as (x) increases.

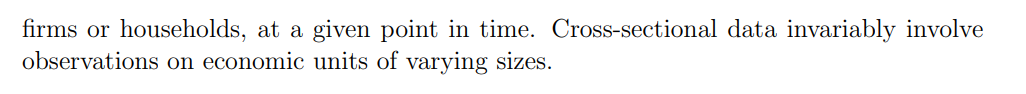
Consequences of heteroskedasticity

the equation (221) is ${\sum }_{i=1}^n(x_i-\bar{x}{)}^2$ in the denominator

the equation (222) is $[{\sum }_{i=1}^n(x_i-\bar{x}{)}^2{]}^2$ in the denominator

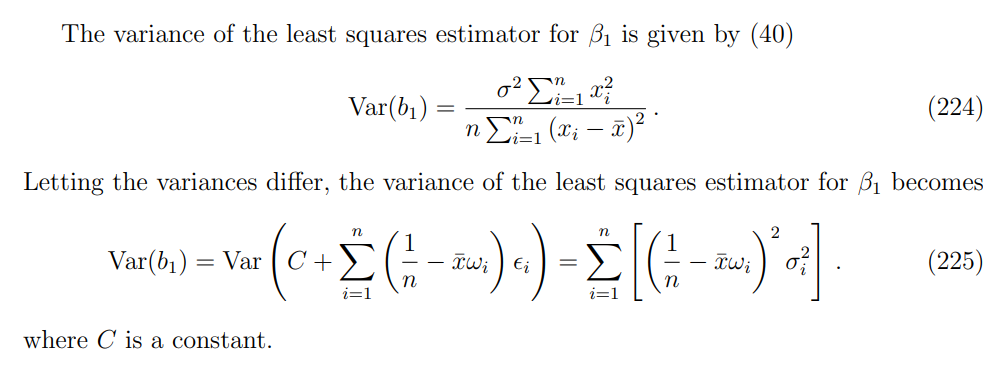
Detecting heteroskedasticity

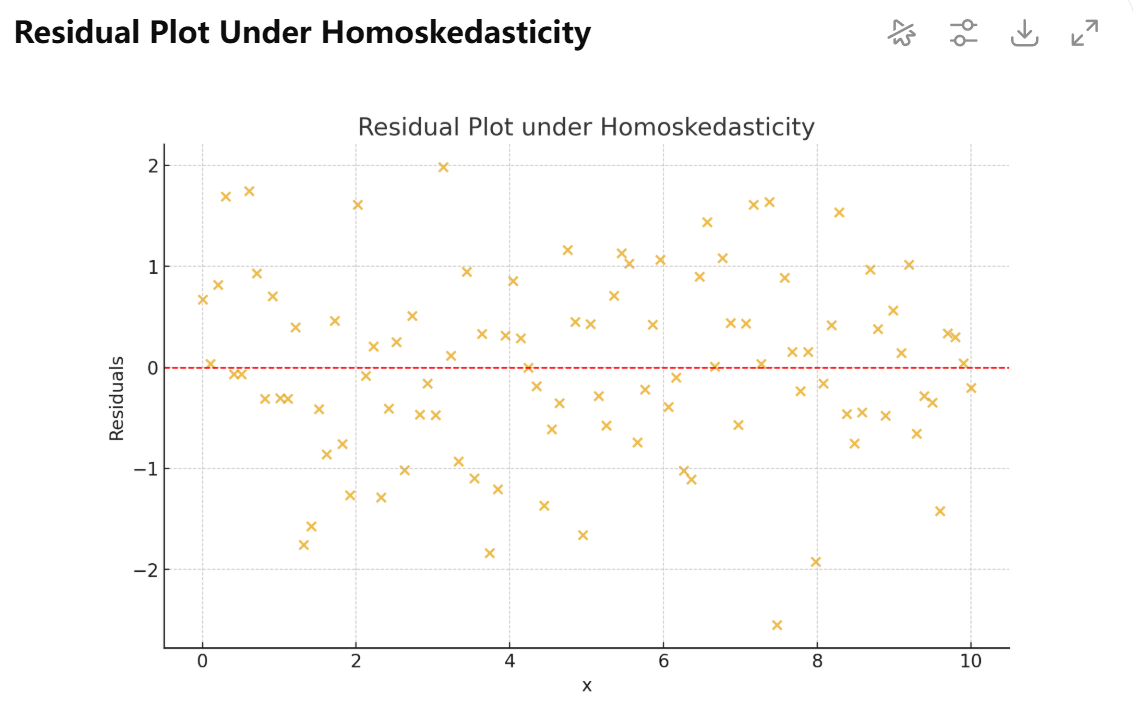
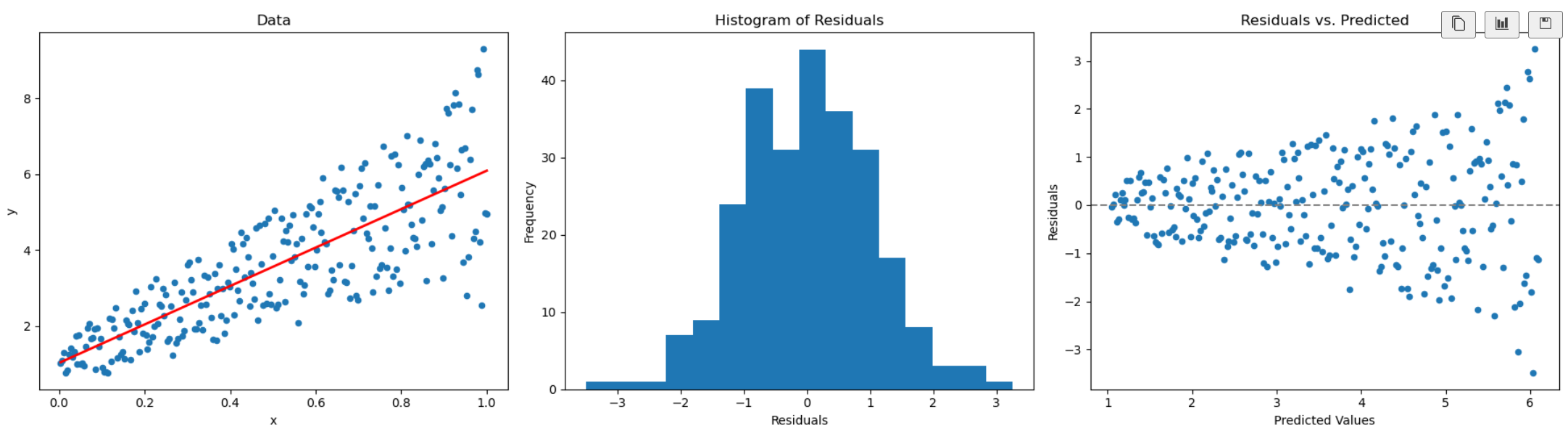
Formal statistical tests

注意这里是对$y_i$的方差，也是error平方的期望.

下面这里是真实的error平方.

The White Test

1. White 检验的特点

• 不需要假设异方差的具体形式：
  和 Breusch–Pagan 不同，BP 假设方差和解释变量的线性关系；White 则允许更一般的关系（比如平方项、交互项），所以更灵活。

• 不要求误差服从正态分布：
  White 检验基于大样本渐近理论，不依赖于正态性假设。

2. 局限性

• 拒绝零假设 ≠ 一定有异方差：
  White 检验本质上是在检验“模型是否被正确设定”。所以如果模型有遗漏变量、函数形式错了，它也可能拒绝零假设。
  换句话说，它可能把“模型设定错误”当成“异方差”。

• 过于一般：

  • 优点：几乎任何形式的异方差都能检测出来。

  • 缺点：敏感度太高，有时会报“假阳性”，让人以为是异方差，实际上是模型设定的问题。